30. Понятие числового ряда и суммы ряда. Геометрическая прогрессия

Рассмотр. бесконечн. посл. чисел Q₁,Q₂,…,Qn₁,… и с помощью этих чисел состав. формальное выражение

Запись (1) назв. числовым рядом, а a_n-общий член ряда.

Сумма ряда. Частичной суммой Sn ряда (1) назв. сумма его первых n-членов. Sn=a₁+a₂+…+a_n.

Если сущ. конечный предел последоват. , то ряд назыв. сходящимся, а числоS-его суммой.

Если предел не сущ. и равен бесконечности, то ряд наз. расходящимся.

Геометрический ряд – это ряд, составл. из членов геометрической прогрессии, т.е. ряд вида:

b₁+b₁q+b₁q²+…+b₁q^n-1+…, b₁

при |q<1| геометрический ряд сх-ся S=b/1-q ; при |q>1|- расх-ся

36. Степенной ряд.Обл-ть сх-ти ст-ого ряда

Опред-ие1:Степенным рядом назв. функциональный ряд вида:

Легко увидеть, что ряд (1) сходится в точке x=0, а ряд (2) в точке x=x₀. Заменой y=x-x₀ исследование сходимости ряда (2) переходит в исследование сходимости ряда (1).

Опред-ие2: Мн-во значений х, при кот-ых степенной ряд (1) сх-ся /расх-ся назыв-ся областью сх-ти /расх-ти степенного ряда.

- Всякий ст-ой ряд имеет свой радикус сх-ти и интервал сх-ти (-R;R)при x=+/-R ряд может сх-ся /расх-ся для каждого конкретного ряда этот «?» решается индивид-но

- областью сх-ти ст-ого ряда (1) явл-ся интервал сх-ти (-R;R)с возм-но присоединённой 1 или 2 точками в зав-ти от того, как ведёт себя ряд на концах интервала.

38. Ряды Тейлора и Маклорена:

Пусть ф-я f(x) опр. в окрестности точки х₀ и имеет в этой точке производные любого порядка.

Ряд вида:

(1) – ряд Тейлора.

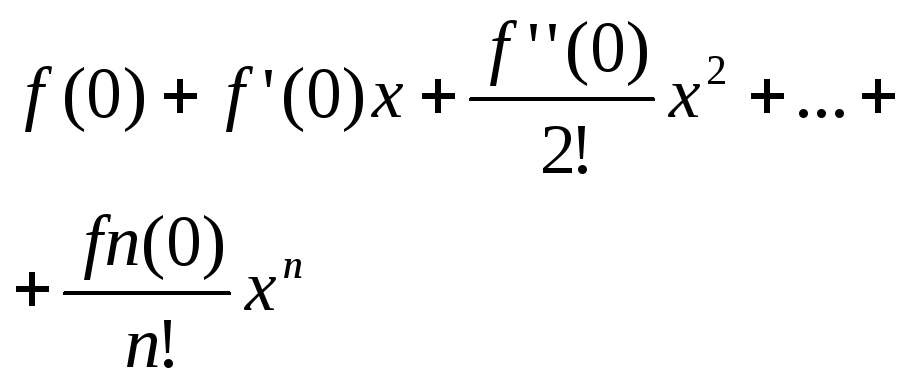(2)

ряд Маклорена.

Достаточным условием разложения в ряд Тейлора явл. ограниченность ф-и и всех ее производных в некоторой окрестности U(x₀) в точке х₀ одним и тем же числом С. |f⁽ⁿ⁾(x)|<C для любого n.

Разложение, тогда для любого х принадлежащего U(x₀) ряд Тейлора ф-и сходится к значению ф-и f(x) в этой точке.

Если ф-я разложима в ряд Тейлора, то это разложение единственно.

6.Нахождение наибольшего и наименьшего значения функции:

- Находим критические точки первого рода;

- Вычисляем значение функции в критических точках и на концах отрезка;

- Среди найденных значений выбираем максимум и минимум.

Если промежуток произвольный, то находим значение функции только в экстремумах.

21. Площадь плоских фигур:

Пусть функция y=f(x) непрерывна и неотрицательна на отрезке [а,в], g(0)≥0.

Рассмотрим криволинейную трапецию, ограниченную графиком функции y=f(x) и прямыми х=а, х=в и у=0.

S такой трапеции: S = , f(x)≥0

Рассмотрим криволинейную трапецию, ограниченную графиком функции y=-f(x), у=0, х=а, х=в.

S такой трапеции: S = , f(x)≤ 0.

Длина дуги кривой:

L=dx

Объем тела вращения:

V=πdx

22. Несобственные интегралы с бесконечными пределами:

Пусть функция f(x) непрерывная в промежутке [a,∞), тогда полагают . Если существует конечный предел, то говорят, что несобственный интеграл сходится, в противном случае интеграл расходится. Аналогично высчитывается на промежутке (-∞,b].

23. Несобственный интеграл от неограниченных функций:

Если функция f(x) не ограничена в любой окрестности точки с промежутка [a,b] и непрерывна в этом промежутке за исключением точки х=с, то полагают .

Если в первой части равенства существуют конечные пределы, то несобственный интеграл сходится, в противном случае – расходится