
- •7.Понятие функции нескольких переменных:
- •8.Частные производные функции нескольких переменных:
- •9.Экстремум функции нескольких переменных:
- •11. Первообразная ф-ии. Св-ва ∫. Таблица
- •12. Замена переменной в неопред-ом интеграле.
- •13. Интегрирование простых дробей
- •14. Интегрирование рациональных дробей
- •15. Интегрирование некоторых иррациональных ф-ий
- •17. Геометрическая задача. Определение опред-ого интеграла.
- •18. Свойства определённых ∫-ов.
- •19. Теорема о существовании первообразной для непрерывной ф-ии. Теорема Ньютона-Лейбница
- •20. Замена переменной и интегрирование по частям в опред-ом интеграле.
- •30. Понятие числового ряда и суммы ряда. Геометрическая прогрессия
- •36. Степенной ряд.Обл-ть сх-ти ст-ого ряда
- •38. Ряды Тейлора и Маклорена:
- •6.Нахождение наибольшего и наименьшего значения функции:
- •21. Площадь плоских фигур:
- •24. Дифференциальные уравнения:
12. Замена переменной в неопред-ом интеграле.
Т-ма1: Пусть дано ∫f(x)dx=F(x)+c (1)
Предположим x=φ(t),тогда ∫f(φ(t))* φ’t(dt)= F(φ(t))+c (2)
Предполагается , что ф-ии f(x), φ(t) непрерывны.
Док-во: По данному F(x)-первообразная для f(x) → F’(x)=f(x). Требуется док-ть рав-во (2), что F(φ(t)) явл-ся первообразной для f(φ(t))*φ’(t). Воспользуемся теоремой о производной сложной ф-ии:
(F(φ(t)))’=F’(φ(t))* φ’(t)= f(φ(t))*φ’(t)
Замечание : Пусть требуется вычислить ∫(1). Если ф-ию F(φ(t)) найти легче, чем F(x), то в рав-ве (1) полагают x=φ(t) и находят ф-ию F(φ(t)). Затем осуществляется переход к старой переменной х и получается искомая ф-ия F(x).
Интегрирование по частям:
Теорема: Пусть ф-ия U(x),V(x) непрерывны вместе со своими производными U’(x),V’(x), тогда на этом промежутке имеет место рав-во:
∫UdV=UV-∫VdU –ф-ла интегрирования по частям.
Она применяется , если ∫VdU вычислить легче, чем ∫UdV
Замечание : Ф-ла (1) применяется для интегрирования выраж-ий след-его вида:
1. ∫Pn(x)sinxdx
2. ∫(Pn(x)cosxdx
3. ∫(Pn(x)axdx
4. ∫(Pn(x)lnm(x)dx
5. ∫(Pn(x)arctgxdx
6. ∫(Pn(x)arcsinxdx
13. Интегрирование простых дробей
Прост. дробями наз. ф-и след вида:
1. A\(x-a), 2. A\(x-a)n, 3. Mx+N\(x2+px+q), 4. Mx+N\(x2+px+q)m,
Где m,n- натуральные числа >1,.
a,p,q,A,M,N – любые действит. числа.
D=p2-4q<0
Дроби вида 1, 2 интегрируются непосредственно.
1.∫A/(x-a)dx=A∫d(x-a)/(x-a)=Aln|x-a|+c
2. ∫ A\(x-a)n=A∫(x-a)-nd(x-a)=A(x-a)-n+1/(-n+1)+C
3. Выделение полного квадрата:
∫4x+1\(x2+x+1)dx=∫(4x+1)dx/((x+1\2)2+3\4)=∫x+1/2=t, x=t-1/2, dx=(t-1/2)’dt, dx=dt]= =∫(4(t-1\2)+1)\(t2+3\4)dt=∫(4t-1)\(t2+3\4)dt=∫4t\(t2+3\4)dt-∫dt\t2+3\4)=2ln(t2+3\4)-1\(3\2)arctgt\(3\2)+C=2ln(x2+x+1)-2\(3)arctg((2x+1)\3)+C
Выражение, кот. содержат квадратный трех член Ax+B\ax2+bx+c; Ax+B\(ax2+bx+c) так же интегрируем выделением полного квадрата трехчлена.
14. Интегрирование рациональных дробей
Опред-ие 1: Рац-ая дробь – отношение двух многочленов P(x)|Q(x), где P и Qимеют действительные коэффициенты.
Опред-ие 2: Рац-ая дробь – правильная, если степень многочлена , стоящего в числительном ниже степени многочлена , стоящего в знаменатиле. В противном случае дробь наз-ся неправильной.
Любую неправильную рац-ую дробь можно представить путём деления суммы многочленов и правильной рациональной дроби.
Теорема о разложении прав. рац. дроби на прост. дроби.
Пусть P(x)\Q(x) – прав. рац. дробь причем знаменатель представлен в виде:
Q(x)=(x-a)n…(x2+px+q)m.
Тогда прав. рац. дробь можно представить в виде суммы простых дробей след. образом:
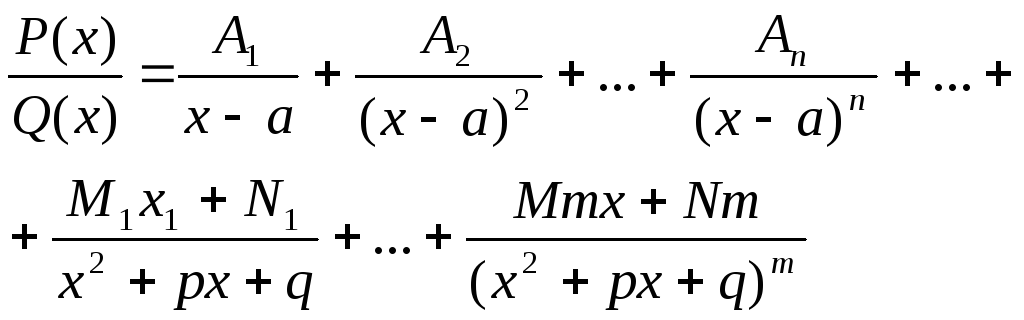
Где a,p,q – действ. числа, p2-4q<0:
A1, A2,..,An; N1, N2, Mm, Nm- неизвестные коэффициенты
15. Интегрирование некоторых иррациональных ф-ий
Рассмотрим интеграл вида:
![]()
Где подинтегральная ф-ия – рац-ая по переменной х
п- натуральное число; a,b,c,d- некоторые постоянные.
∫-лы такого вида могут быть вычислены способом подстановки :
![]()
Таким образом:
![]()
Под интегралом получили рациональную дробь.
Частные случаи:
1.
c=0,
d=1→![]()
![]()
2. a=1, b=0, c=0,d=1
![]()
![]()
