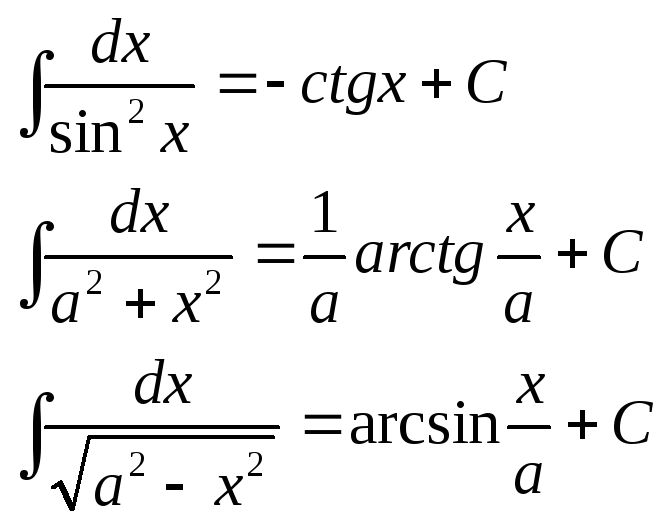1.

Теорема Ролля:

Пусть задана функция у=f(x), удовлетворяющая следующим условиям:

- Определена и непрерывна на [а,в];

- Дифференцируема на (а,в);

- Имеет равные значения на концах отрезка: f(a)=f(в)

Тогда найдется такая т. с (a<c<в), что выполняется равенство f’(c)=0.

Теорема Лагранжа:

Пусть задана функция у=f(x), удовлетворяющая первым двум условиям теоремы Ролля, тогда существует т. с (a<c<в), что выполняется равенство (f(в)-f(a))/(в-а)=f’(c).

Теорема Коши:

Пусть заданы функции f(x) и g(x), удовлетворяющие условиям:

- Определены и непрерывны на [а,в];

- Существуют производные f’(x) и g’(x) на (а,в);

- G’(x) не равно 0.

Тогда найдется такая т. с (a<c<в), что выполняется равенство (f(c)-f(a))/(g(в)-g(a))=f’(c)/g’(c).

2.

Теорема (необходимое и достаточное условие постоянства функции):

Пусть у=f(х) определена и непрерывна на множестве Х и внутри этого множества имеет конечную производную f’(x), на границе множества сохраняет непрерывность, если принадлежит Х.

Для того, чтобы f(x) была const на множестве Х, необходимо, чтобы f’(x)=0 внутри множества Х.

Достаточные условия возрастания и убывания функции:

Для того, чтобы f(x) была возрастающей (убывающей), достаточно чтобы f’(x)>0 (f’(x)<0) для всех х, принадлежащих множеству Х.

3.

1ое достаточное условие экстремума функции:

Пусть х₀ – критическая точка 1ого рода. Предположим, что у=f(x) дифференцируема в некоторой окрестности (х₀-δ,х₀+δ) и f’(x) сохраняет свой знак слева и справа от х₀.

Значит: если при переходе через х₀ f’(x) меняет знак с + на -, то в т. х₀ f(x) имеет максимум, если с – на +, то минимум, если знак не меняется, то х₀ не является экстремумом.

2ое достаточное условие экстремума функции:

Пусть х₀ – стационарная точкам, в которой f(x) дважды дифференцируема, тогда если f”(х)<0, то х₀ – максимум, f”(х)>0, то х₀ – минимум (если равно 0, то не работает).

4.______

Пусть у=f(x) дифференцируема на (а,в), графиком ее является некоторая кривая.

Выпуклость кривой:Кривая у=f(x) называется выпуклой на (а,в), если все точки кривой лежат ниже любой ее касательной на этом интервале.

Вогнутость кривой:Кривая у=f(x) называется вогнутой на (а,в), если все точки кривой лежат выше любой ее касательной на этом интервале.

Точки перегиба:Точки, в которых выпуклость сменяется на вогнутость и наоборот, называются точками перегиба.

Теорема (достаточное условие выпуклости/вогнутости):

Пусть у=f(x) дважды дифференцируема на промежутке (а,в), тогда:

Если на (а,в) f”(x)>0, то кривая вогнутая;

Если на (а,в) f”(x)<0, то кривая выпуклая.

Теорема (достаточное условие перегиба):

Пусть х₀ – критическая точка 2ого рода, тогда:

Если при переходе через т. х₀ f” меняет знак с + на -, то х₀ – т. перегиб

Если с – на +, то выпуклость на вогнутость.

7.Понятие функции нескольких переменных:

Рассмотрим множество D, состоящее из пар действительных чисел (х,у). Любую пару чисел можно изобразить на плоскости точкой.

Если каждой паре действительных чисел соответствует одно определенное число z€Z, то говорят, что на множестве D задана функция z=f(x,y) со значениями во множестве Z.

Функцию z=f(x,y) называют функцией двух переменных, а переменные х и у – независимыми переменными.

Определение предела и непрерывности функции двух переменных:

Пусть функция f(x,y) определена внутри некоторой окрестности точки (х₀,у₀) кроме, может быть, самой точки.

Число А называется пределом функции z=f(x,y) в точке М₀ (х₀,у₀), если для любой последовательности точек {(x_n,y_n)} области определения функции, отличных от (х₀,у₀) и сходящихся к (х₀,у₀), последовательность значений функции {(x_n,y_n)} сходится к А:

=A.

Если =f(х₀,у₀), то функция f(x,y) называется непрерывной в точке (х₀,у₀).

8.Частные производные функции нескольких переменных:

Если существует предел

,

то он называется частной производной функции z по х в точке и обозначается символами или

.

Аналогично определяется частная производная по у: ₌=

Полный дифференциал функции нескольких переменных:

Полным дифференциалом функции z=f(x,y) называется выражение вида dz = (x,y)dx + (x,y)dy, где dx=∆х, dy=∆у.

Является суммой частных дифференциалов.

9.Экстремум функции нескольких переменных:

Функция z=f(x,y) имеет в точке М₀ (х₀,у₀) максимум (минимум) f(х₀,у₀), если вблизи этой точки для всех точек М, отличных от М₀, выполняется условие:

- f(x,y)< f(х₀,у₀) – max

- f(x,y)>f(х₀,у₀) – min

Необходимые условия экстремумов:

Если точка (х₀,у₀) – точка экстремума функции z=f(x,y) и в ней существуют обе частные производные, то производные в точке (х₀,у₀) равны нулю.

=0 =0

10.Ф-лы , которые служат для предоставления опытных данных называются эмпирическими. В большинстве случаев хар-р зависимости между переменными предполагается известным и остаётся только опред-ть пар-ры самой ф-лы.

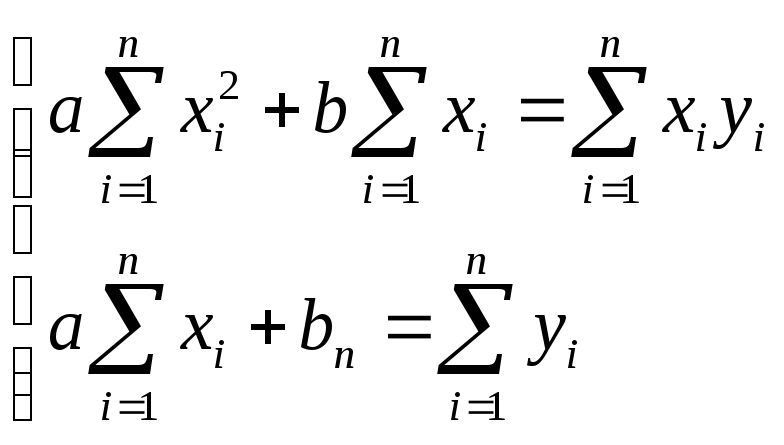
Получаемая система назв. «нормальной системой выравнивание эмпирических данных» по методу наим. квадратов вдоль прямой. Решая эту систему получаем значение параметров a и b, при кот. ф-я Ф’ab достигает минимума и прямая y=kx+b будет проведена наилучшим образом. Проведем группировку относительно a,b,c.

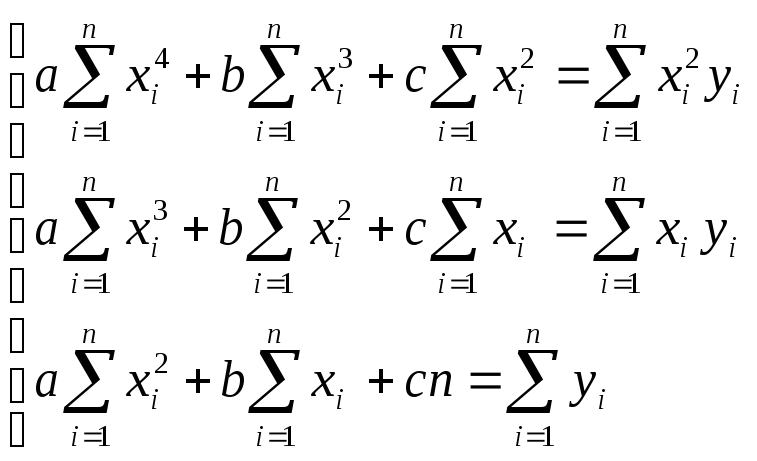получ. сист. наз. «норм. сист. выравн. эмпирич. Данных по методу наим. квадр. вдоль параболы».

Решая ее получаем значение a,b,c, которые доставляют минимум ф-и Ф от a,b,c, и для которых парабола y=ax²+bx+c будет проведена и наилучшим образом.

Аналогичным способом могут быть установл. и др. виды зависимости между данными эмпирического поля.

11. Первообразная ф-ии. Св-ва ∫. Таблица

Опред-ие 1:Ф-ия F(x)-первообразная для ф-ии f(x) на некотором промежутке, если для всех х из этого промежутка выполняется рав-во F’(x)= f(x)

Опред-ие 2: Семейство всех п-ых для ф-ии f(x) на некотором промежутке называется неопределённым интегралом от ф-ии f(x) на это промежутке и обозначается

∫ f(x)dx=F(x)+c

Иначе неопределенный интеграл от ф-и это совокупность всех первообр. для этой функции.

Свойствa: 1.производная от неопределенного интеграла равна подынтегральной ф-и, которая явл. критерием правильности вычисления неопр. интеграла. (∫f(x)dx)’=(F(x)+C)’=f(x)

2. Неопр. интеграл от алгебраической суммы двух или более ф-й равен алгебр. cумме неопр. интегралов от этих ф-й. ∫=∫₁+∫₂

3. Постоянный множитель можно вынести за знак неопр. интеграла. ∫kf(x)dx=k∫f(x)dx

Таблица основных интегралов: