
ДЗ Задача №4 МВ Графічний метод
.pdfвизначенні оптимуму типу мінімум і зверху при визначенні оптимуму типу максимум.
Теорема. Якщо задача лінійного програмування має оптимальний план, то він досягається у вершинах опуклого багатогранного тіла, що є областю допустимих розв’язків або планів. Якщо ж оптимальний план досягається більш ніж в одній вершині, то він досягається в будь-якій точці опуклої лінійної комбінації відповідних вершин многогранника.
4. Опорні плани задачі лінійного програмування
Розглянемо канонічну форму запису ЗЛП:
F с1x1 |
с2 x2 |
... сn хn |
opt . |
||||||||||||
a |
x a |
x |
... a |
x |
|
b , |
|
||||||||
|
11 |
1 |
12 |
|
2 |
|
|
1n |
n |
|
|
1 |
|
||
a21x1 a22x2 |
|
... a2n xn |
b2 |
, |
|||||||||||
|
|
||||||||||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
x a |
|
x |
2 |
... a |
|
x |
n |
b |
|
|||||
|
m1 1 |
m2 |
|
|
|
mn |
|
|
m |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
x j |
0 |
j 1, n . |
|
|
|
|||||||
(4)
(5)
(6)
Щоб мало сенс говорити про оптимальний план задачі (4) – (6), необхідно й достатньо, щоб система обмежень (5) була сумісна в області ненегативних значень змінних.
Тому що в системі лінійних рівнянь (5) m рівнянь й n змінних, то ранг r системи повинен бути менше числа змінних (r<n). У такому випадку серед змінних r змінних – базисні, а (n-r) змінних – вільні
Визначення. Опорним планом задачі лінійного програмування називається такий план, у якому базисні змінні ненегативні, а вільні дорівнюють нулю.
З визначення витікає, що кількість додатних компонент в опорних планах не повинне перевищувати рангу системи обмежень.
4.1. Геометрична інтерпретація опорних планів
Відомо, що плани задачі лінійного програмування із погляду геометрії можна трактувати, як геометричне місце опуклого багатогранного тіла, що є ОДР задачі. Тоді опорні плани задачі із погляду геометрії можна трактувати як вершини цього багатогранного тіла.
Теорема. Кожному опорному плану ЗЛП відповідає вершина багатогранника Ω і навпаки, кожній вершині багатогранника Ω відповідає опорний план.
Таким чином, оптимальні плани варто шукати серед опорних планів (тобто серед вершин опуклого багатогранного тіла).
10

5. Приклади застосування графічного методу
Для розв’язування двовимірних задач лінійного програмування (ЛП), а також деяких тривимірних і n -вимірних задач застосовується графічний метод, що ґрунтується на геометричній інтерпретації та аналітичних властивостях задач ЛП.
Постановка двовимірної задачі лінійного програмування. Розглянемо двовимірну задачу ЛП:
F c1x1 c2 x2 |
max min . |
(7) |
||||
за умов: |
|
|
|
|
|
|
a11x1 a12x2 |
, , b1 |
|
|
|||
a x a |
x |
, , b |
|
|
||
21 1 |
22 2 |
|
2 |
. |
|
|
................................ |
|
(8) |
||||
|
|
|
, , b |
|
|
|
a x a |
x |
|
|
|||
m1 1 |
m2 |
|
2 |
m |
|
|
x1 0, x2 0. |
|
|
(9) |
|||
Припустимо, що система (8) за умов (9) сумісна і многокутник її розв’язків обмежений.
Кожне i -те обмеження-нерівність (8) визначає півплощину з граничною прямою ai1x1 ai 2 x2 bi , i 1, m. Системою обмежень (8) описується
спільна частина, або переріз усіх зазначених півплощин, тобто множина точок, координати яких задовольняють всі обмеження задачі.
Цільова функція задачі лінійного програмування геометрично інтерпретується як сім’я паралельних прямих c1x1 c2 x2 const .
Як зазначалося вище, розв’язати задачу лінійного програмування графічно означає знайти таку вершину багатокутника розв’язків, у результаті підстановки координат якої в (7) лінійна цільова функція набуває найбільшого (найменшого) значення.
Використовуючи алгоритм графічного методу:
1.Будують простір допустимих розв’язків, які задовольняють усі обмеження моделі:
o будують прямі лінії, рівняння яких дістають заміною в обмеженнях задачі (8) знаків нерівностей на знаки рівностей;
o визначають півплощини, що відповідають кожному обмеженню задачі.
2.Знаходять оптимальний розв’язок серед усіх точок простору допустимих розв’язків:
|
будують радіус-вектор |
|
c1,c2 , що задає напрям зростання значень |
||||||
o |
F |
||||||||
|
цільової функції задачі; |
||||||||
|
будують пряму c1x1 c2 x2 const , перпендикулярну до вектора |
|
; |
||||||
o |
F |
||||||||
o |
переміщуючи пряму |
c1x1 c2 x2 const (паралельним перенесенням) в |
|||||||
|
напрямі |
вектора |
|
|
(для задачі максимізації) або в протилежному |
||||
|
F |
||||||||
|
напрямі |
(для задачі |
мінімізації), знаходять вершину многокутника |
||||||
|
|
|
|
|
11 |
|
|
||

розв’язків, де цільова функція досягає екстремального значення (крайню вершину многокутника у потрібному напрямі);
o визначають координати точки, в якій цільова функція набуває максимального (мінімального) значення, і обчислюють екстремальне значення цільової функції в цій точці.
Слід зауважити, що за допомогою графічного методу можна розв’язати задачу лінійного програмування, система обмежень якої містить n невідомих та m лінійно незалежних рівнянь, якщо n і m пов’язані співвідношенням n m 2.
Для застосування графічного методу до таких задач, необхідно зробити m повних виключень змінних з системи методом ЖорданаГаусса. Скориставшись умовою невід’ємності змінних задачі перейти до задачі ЛП із двома змінними. Розв’язати отриману задачу графічно, та, за знайденим оптимальним розв’язком, знайти m змінних, які залишились.
Приклад 2. Задачу лінійного програмування розв’язати графічним методом. Максимізувати F 5x1 2x2 при виконанні обмежень:
2x1 3x2 10 , x1 2x2 6 , x1 0, x2 0 .
Розв’язання. Побудуємо простір допустимих розв’язків (рис. 8). Для цього побудуємо прямі лінії, рівняння яких одержимо в результаті заміни в обмеженнях знаків нерівності на знаки рівності. Потім визначаємо допустиму півплощину для кожного рівняння за допомогою “тестової точки”, яка не належить відповідній прямій. Щоб визначити необхідну півплощину (на рис. 8 її напрям позначено стрілкою), потрібно взяти будь-яку точку і перевірити, чи задовольняють її координати зазначене обмеження. Якщо задовольняють, то півплощина, в якій міститься вибрана точка, є геометричним зображенням нерівності. У протилежному разі таким зображенням є інша півплощина. Умова невід’ємності змінних x1 0, x2 0 обмежує область допустимих планів задачі першим
квадрантом системи координат (рис. 8). Переріз усіх півплощин визначає область допустимих планів задачі (рис. 9).
Позначимо відповідні рівності системи обмежень
2x1 3x2 |
10 |
, |
1 |
|
|
|
|
|
|
x1 2x2 |
6 , |
|
2 |
|
x1 |
0 , |
|
3 |
|
x2 |
0 . |
|
4 |
|
|
|
|
|
|
12 |
|
|
|
|
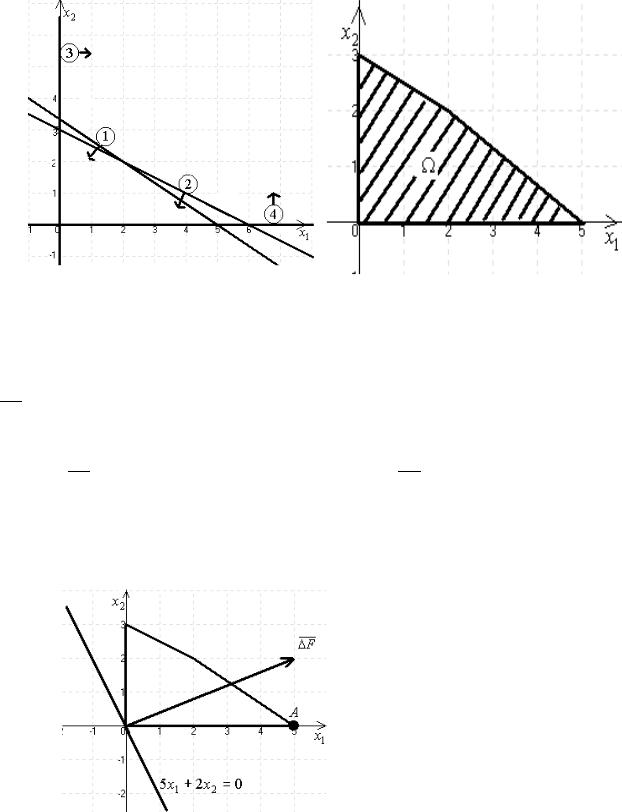
Таким чином, ми отримали многокутник розв’язків задачі лінійного програмування (рис. 9).
Рис. 8 |
Рис. 9 |
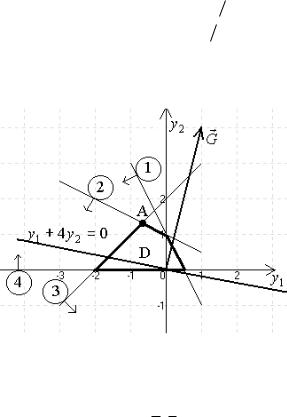
Переходимо до етапу знаходження оптимального розв’язку серед усіх точок простору допустимих. Для цього будуємо радіус-векторF 5,2 , координати якого складаються з коефіцієнтів при змінних у цільовій функції. Цей вектор задає напрям зростання значень цільової функції задачі. Далі будуємо пряму 5x1 2x2 const , перпендикулярну до вектора F . Переміщуючи її в напрямі вектора F , знаходимо вершину багатокутника , де цільова функція досягає максимального значення. Після чого визначаємо координати знайденої точки і обчислюємо значення цільової функції F у ній.
Знайдена точка A (рис. 10) буде точкою максимуму. Координати цієї точки можна знайти з рис. 8 (тобто розв’язати графічно) або розв’язавши
систему 2x1 3x2 10,
x2 0,
|
(оскільки точка A є |
|
Рис. 10 |
точкою перетину прямих |
|
(1) та (4) ). |
||
|
||
|
Таким чином, ми |
|
|
13 |
знайшли точку A 5,0 , яка є точкою максимуму для функції F в області, причому F 5,0 25 .
Відповідь: точка максимуму A 5,0 , Fmax 25 .
Приклад 3. Задачу лінійного програмування розв’яжемо графічним методом.
g y1 4y2 max ,
2 y1 |
y2 |
1, |
|
|
2, |
y1 2 y2 |
||
|
y2 |
2, |
y1 |
||
y2 0 .
Розв’язання. Зауважимо, що оскільки на змінну y1 в умові задачі не
накладено обмеження невід’ємності, то вона може мати будь-який знак (вільна за знаком).
Скористаємось алгоритмом (рис. 11).
Найбільшого значення цільова функція g досягає в точці А. Знайдемо її координати, як перетин другого та третього рівнянь системи
|
|
|
|
|
|
|
|
|
|
|
y 2 y |
|
|
2, |
|
|
y 2 3, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
2, |
|
|
1 |
4 3. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
y |
2 |
|
|
|
y |
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||
|
* |
|
|
2 |
|
4 |
|
|
* |
|
|
|
2 |
|
|
|
4 |
|
14 |
|
|
|
||||
Тобто Y |
|
|
|
|
, |
|
|
, |
g Y |
|
1 |
|
|
|
4 |
|
|
|
|
|
. |
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
3 |
|
3 |
|
|
|
|
|
|
3 |
|
|
|
3 |
|
3 |
|
|
|
|
|||
Рис. 11
Відповідь: точка максимуму A 23 , 43 , gmax 143 .
Приклад 4. Розв’язати задачу ЛП графічним методом (для n змінних)
14

z 2x1 x2 x3 3x4 4x5 max
за умов:
x1 x2 3x3 18x4 2x5 4,
2x1 x2 4x3 21x4 4x5 22,3x1 2x2 8x3 43x4 11x5 38,
xi 0 , i 1,5 .
Розв’язання. Для нашого прикладу необхідне співвідношення виконується, бо n 5 , а m 3 .
Використовуючи метод Жордана-Гаусса, зробимо три повних
виключення невідомих x1 , x2 , |
x3 . У результаті отримаємо таку систему |
||||||
|
x |
x |
|
3x |
|
6, |
|
|
1 |
|
4 |
|
|
5 |
|
|
x2 |
7x4 |
10x5 70, |
||||
|
|
4x4 |
5x5 20, |
||||
|
x3 |
||||||
звідки x1 6 x4 3x5 , |
x2 70 7x4 10x5 , |
x3 20 4x4 5x5 . Якщо підставити ці |
|||||
значення у цільову функцію і виключити з останньої системи базисні
змінні x1 , x2 , x3 , отримаємо задачу, |
яка виражається тільки через вільні |
|
змінні x4 та x5 . Отримана задача має вигляд: |
||
z 6x4 15x5 |
38 max |
|
за умов |
|
|
x |
3x |
6, |
4 |
5 |
|
7x4 10x5 70, |
||
4x 5x 20, |
||
|
4 |
5 |
x4 0, |
x5 0 . |
|
Задача залежить від двох змінних. Скористаємося графічним методом розв’язання задачі лінійного програмування.
Побудуємо область допустимих розв’язків D (рис. 12). Пронумеруємо рівняння таким чином:
x4 3x5 6, |
1 |
||
|
|
70, |
2 |
7x4 10x5 |
|||
|
|
20, |
3 |
4x4 5x5 |
|||
x4 |
0, |
|
4 |
|
|
|
5 |
|
0. |
|
|
x5 |
|
||
|
15 |
|
|
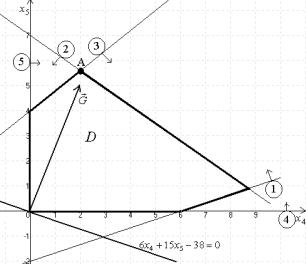
Рис. 12
З рис. 12 видно, що функція z набуває максимального значення в кутовій точці А, яка лежить на перетині прямих (2) та (3). Розв’язавши систему
|
|
|
|
|
|
|
|
|
|
|
7x4 10x5 70, |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5x |
20, |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
4x |
4 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
знаходимо x |
|
2 , |
x |
28 |
. |
Максимальне |
значення функції в |
цій точці |
|||||||||||||
4 |
|
|
|||||||||||||||||||
|
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
дорівнює zmax |
z(A) 38 12 84 58 . |
|
|
|
|
|
|
|
|||||||||||||
Для знаходження оптимального плану вихідної задачі підставимо |
|||||||||||||||||||||
знайдені значення x4 |
|
|
та |
x5 |
у |
вирази |
x1 , |
x2 , x3 . Звідки |
отримаємо |
||||||||||||
розв’язок задачі x |
|
104 |
, |
x |
|
0 |
, x |
0 , x |
|
2 , x |
|
28 |
. |
|
|||||||
|
|
2 |
4 |
|
|
||||||||||||||||
|
|
1 |
5 |
|
|
|
|
|
3 |
|
|
|
|
5 |
5 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Відповідь: zmax 58 у точці X |
* 104 , 0, 0, 2, |
28 . |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
5 |
|
|
|
Приклад 5. (використання електронних таблиць MS Excel)
Завдання. Скласти математичну модель задачі. Розв’язати її графічно та за допомогою електронних таблиць Microsoft Excel (без урахування умови цілочисловості). Порівняти отримані результати.
Умова задачі. Для виробництва двох видів продукції А і В використовується два види ресурсів. Норми витрат ресурсів на кг продукції, а також прибуток від реалізації наводяться в таблиці:
16
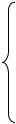
|
Норми витрат ресурсу на кг продукції, |
Прибуток від |
||
Продукція |
|
кг |
реалізації кг |
|
|
І |
|
ІІ |
продукції, грн |
А |
1 |
|
2 |
3 |
В |
2 |
|
1 |
2 |
Обсяг ресурсу |
6 |
|
8 |
|
на складі, кг |
|
|
||
|
|
|
|
|
Відомо, що кількість кг продукції А повинна бути більшою за кількість кг продукції В принаймні на 1 кг. Кількість кг виготовленої продукції В не повинна перевищувати 2 кг.
Знайти план випуску виробів А і В, що забезпечує найбільший прибуток від їх реалізації. У відповіді вказати найбільший прибуток.
Розв’язання. Побудуємо математичну модель задачі.
Нехай x1 – кількість кг виготовленої продукції А, а x2 – кількість кг виготовленої продукції В. Цільова функція має вигляд
F x1, x2 3x1 2x2 max .
Обмеження на ресурси мають вигляд:
x1 2x2 6 ,
2x1 x2 8 .
Обмеження на кількість виготовленої продукції мають вигляд
x1 1 x2 , або x1 x2 |
1, |
x2 2 . |
|
Добавляємо уявну умову невід’ємності змінних та отримаємо |
|
математичну модель. Знайти |
|
F x1, x2 3x1 2x2 max , |
|
за умов |
|
x1 2x2 6, |
(1) |
2x1 x2 8 , |
(2) |
x1 x2 1, |
(3) |
x2 2 , |
(4) |
x1 0, x2 0.
Побудуємо прямі обмежень, для чого обчислимо координати точок перетину цих прямих з осями координат (рис. 13).
17
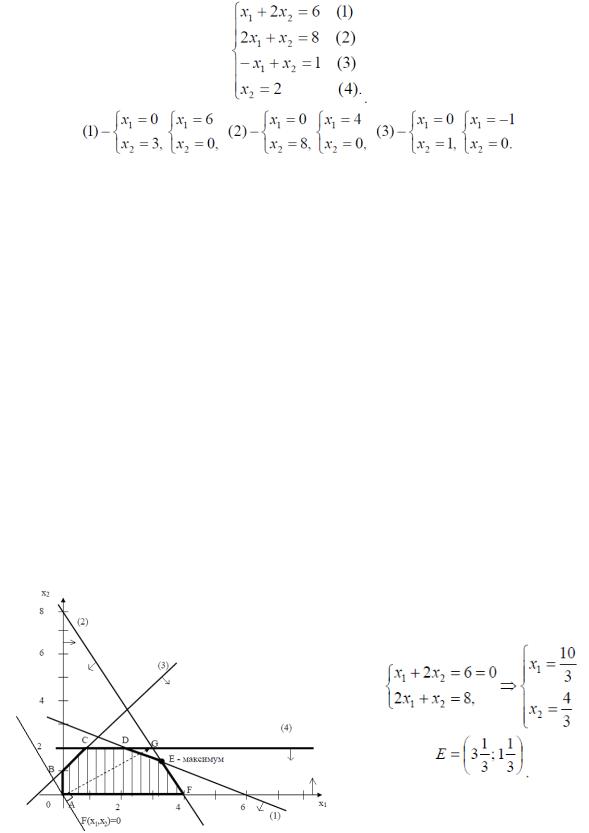
Пряма (4) проходить через точку x2 = 2 паралельно осі x1. Визначимо область допустимих розв’язків. Наприклад, підставимо точку (0; 0) у вихідне обмеження (3), дістанемо 0 < 1, що є істинною нерівністю, тому стрілкою позначимо півплощину, що містить точку (0; 0), тобто розташовану правіше і нижче прямої (3). Аналогічно визначимо допустимі півплощини для інших обмежень і вкажемо їх стрілками біля відповідних прямих обмежень. Загальною областю, дозволеною всіма обмеженнями, тобто областю допустимих розв’язків є багатокутник ABCDEF (рис. 13).
Будуємо градієнт G з точки (0; 0) у точку (3; 2), так як цільова функція лінійна і значення частинних похідних будуть дорівнювати значенням коефіцієнтів при керованих змінних цільової функції. Лінії рівня цільової функції завжди перпендикулярні до вектора G.
Точка Е – це остання вершина багатокутника допустимих розв’язків ABCDEF, через яку проходить лінія рівня цільової функції, рухаючись за напрямком вектора G. Тому Е – це точка максимуму цільової функції. Визначимо координати точки Е з системи рівнянь прямих обмежень (1) і
(2):
Рис. 13
Максимальне значення цільової функції дорівнює:
18
F * 3 103 2 43 12 23 .
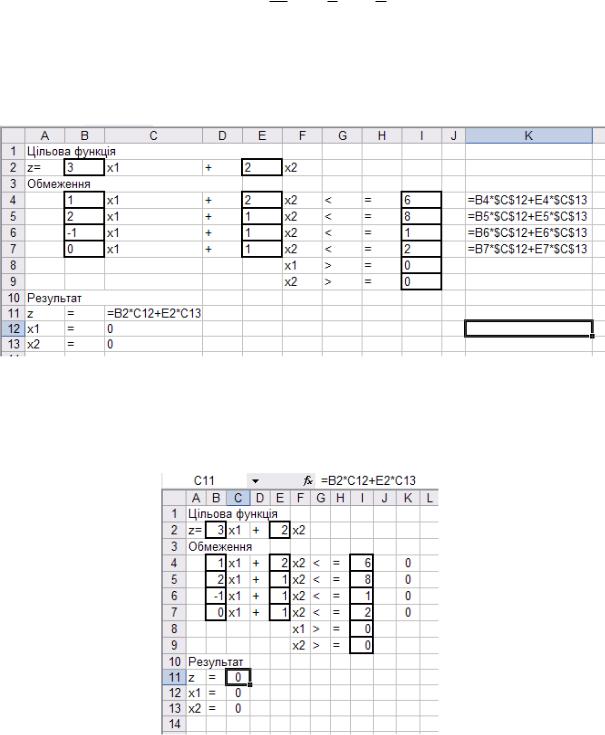
Розв’яжемо дану задачу за допомогою електронних таблиць Microsoft Excel, занесемо усю необхідну інформацію на аркуш Microsoft Excel (рис. 14).
Рис. 14 – Вигляд вихідних даних задач з реалізованими формулами
Перед запуском Поиск решений маємо дані, які подано на рис. 15
Рис. 15 – Вихідні дані задачі
Запускаємо Поиск решений та заносимо усю необхідну інформацію, як показано на рис. 16. Отримаємо результат, який подано на рис. 17.
19
