Тема 5 геометричні характеристики плоских фігур

5.1. Уявлення про статичний момент площі. Визначення центра ваги плоскої фігури

Однією з найбільш розповсюджених геометричних характеристик плоскої фігури є її площа . Площа при осьовому розтяганні і стисканні є геометричним чинником міцності: чим більша площа поперечного перерізу елемента конструкції, що розтягується, тим менша величина напружень, що виникають у стержні. Площа поперечного перерізу є також геометричним фактором жорсткості деформованого елемента конструкції при його розтяганні. Чим більша площа поперечного перерізу, тим менше подовження стержня. Однак площа поперечного перерізу не може бути геометричним фактором міцності і жорсткості для таких видів деформації як згинання, кручення, для деяких складних видів деформації. Тому познайомимося з деякими іншими видами геометричних характеристик плоских фігур. Однією з таких характеристик єстатичний момент площі.

Розглянемо плоску фігуру довільної форми (Рис.5.1). Виберемо початок координат і задамо положення в цій системі нескінченно малої площі координатамиі.

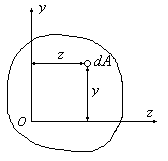
Рис.5.1

Величини, що дорівнюють інтегральній сумі добутку елементарної площі на координату:

і (5.1)

називаються відповідно осьовими моментами площі фігури відносно осей і. Розмірність статичного моменту площі – (довжина)³.

Статичні моменти площі простої фігури, положення центра ваги якої заздалегідь відомо, відносно обраних осей і(Рис.5.2) знайдемо з формул:

; , (5.2)

де і координати цетра ваги фігури в обраній системі координат.

Рис.5.2

З рис.5.2 добре видно, що статичні моменти фігури відносно осей і, що проходять через центр ваги фігури, дорівнюватимуть нулю. У цьому основна властивість статичного моменту площі:статичний момент площі відносно будь-якої осі, що проходить через центр ваги фігури, дорівнює нулю.

З виразів (5.2) можна одержати ще один важливий висновок. Виявляється, з цих формул можна одержати вирази для визначення положення центра ваги фігури:

; . (5.3)

Використовуючи ці формули можна визначати положення центра ваги складних фігур. Розглянемо приклад розв’язання такої задачі.

Приклад 5.1. Знайти положення центра ваги фігури, що має форму тавра (Рис.5.3).

Розв’язок:

1. Розіб’ємо зображену на рис.5.3 фігуру на прості і привласнимо їм номери 1 і 2. Центр ваги кожної з простих фігур позначимо відповідно і.

2. Проведемо через центри ваги кожної з фігур осі ,і вісь. Вісьє віссю симетрії фігури, проходить через центри ваги обох простих фігур і усієї фігури також і тому індексації не має.

3. Вибираємо за початок координат центр ваги другої фігури іяк вісь, відносно якого будемо виконувати всі обчислення.

4. Обчислимо статичний момент площі фігури відносно осі :

см³. (а)

Рис.5.3

У формулі (а) координата центра ваги другої простої фігури , тому що вісь, відносно якої визначався статичний момент площі, проходить через центр ваги другої фігури. Відповідно до основної ознаки статичний момент відносно будь-якої центральної осі дорівнює нулю. У зв'язку з цим для скорочення арифметичних обчислень при визначенні центра ваги складних фігур можна рекомендувати вибирати в якості початку координат центр ваги однієї з простих фігур.

4. Знаходимо координату центра ваги усієї фігури, використовуючи вираз (5.3):

см.

Знайдене значення координати центра ваги відкладемо уздовж осі вгору від точки, тому що це значення додатне. Отриману точку позначимо буквою. Вісь, проведена через центр ваги усієї фігури, буде однією з центральних осей фігури. Друга центральна вісь фігури в даному прикладі не визначається, тому що цією віссю є вісь симетрії. Статичні моментипростих фігур і усієї фігури відносно цієї осі дорівнюють нулю. Відповідно до виразу (5.3) координата центра ваги усієї фігури.

Аналізуючи отриманий розв’язок, можна зробити висновок про те, що при визначенні центра ваги для складних фігур дуже важливо вдало вибрати початок координат і вісі, відносно яких виконуються всі обчислення. Як відзначалося вище, початок координат варто поміщати в центр ваги однієї з простих фігур.