16.1.4. Класифікація коливань за характером деформації пружних елементів конструкцій

Відповідно до цієї класифікації стосовно стержневих систем розрізняють поздовжні, поперечні і крутильні коливання.

При поздовжніх коливаннях переміщення всіх точок пружного стержня спрямовані уздовж осі стержня. При цьому має місце деформація подовження або укорочення стержня, тобто поздовжні коливання можна назвати коливаннями розтягання-стискання.

Поперечними коливаннями називаються коливання згинання, при яких прогини спрямовані перпендикулярно до осі стержня. Напружений стан при поперечних коливаннях, очевидно, буде такий самий, як і при статичному згинанні балки. Тому поперечні коливання інакше можна назвати коливаннями при згинанні.

Крутильними називаються коливання стержнів, які супроводжуються змінною деформацією кручення. Ці коливання виникають в різного роду валах, що працюють на кручення.

Окрім перерахованих видів коливань існують коливання змішаного типу, при яких одночасно виникають деформації згинання і кручення, так звані згинно-крутильні коливання.

16.2. Власні коливання системи з одним ступенем вільності

Розглянемо балку з однією зосередженою масою , прикріпленою до якої-небудь точки на відстані від лівої опори (Рис.16.4,а).

Рис.16.4

Під вагою спочатку прикладеного вантажу балка прогнеться на величину і дістане стану (16.4,б), який назвемо станом рівноваги. Відносно цього стану надалі балка здійснюватиме коливання.

Припустимо, що маса балки у порівнянні з масою мала, і нею можна нехтувати. Вісь зігнутої осі балки визначається в цьому випадку величиною відхилення маси, тобто тільки одним параметром. Тому таку балку називають системою з одним ступенем вільності.

Якщо масу відхилити від стану рівноваги (Рис.16.4,в) і відпустити, то балка разом з масою почне коливатися біля стану рівноваги. Внаслідок дії сил опору коливання поступово затухатимуть, і через деякий час балка знов повернеться у свій початковий стан рівноваги (Рис.16.4,б).

Одержимо рівняння коливань заданої системи [6]. Відхилення маси від стану рівноваги відбувається за рахунок сил інерції. Введемо одиничне переміщення від сили інерції, що дорівнює одиниці. Складемо співвідношення:

(16.1)

Враховуючи, що сила інерції дорівнює

,

з співвідношення (16.1) знайдемо величину відхилення маси від первинного стану рівноваги:

(16.2)

Оскільки , перепишемо рівняння (16.2) у вигляді:

. (16.3)

Позначимо , де  колова частота власних коливань, і підставляючи в (16.3), остаточно одержимо диференціальне рівняння, яке описує даний коливальний процес:

. (16.4)

Рівняння (16.4) є лінійним диференціальним рівнянням другого порядку без правої частини. Розв’язок такого рівняння шукатимемо у вигляді:

, (16.5)

де і  сталі інтегрування.

Рівняння (16.5) можна привести до іншого вигляду. Для цього введемо позначення ; і підставимо у рівняння (16.5). Одержимо:

, (16.6)

де  амплітуда коливань;  початкова фаза коливань.

Визначимо амплітуду коливань і початкову фазу . Для цього запишемо вирази для швидкості рухомої маси:

. (16.7)

Скористаємося граничними умовами для визначення параметрів та . Припустимо, що при

; .

Тоді з рівнянь (16.1) та (16.7) знайдемо:

;

.

Розв’язуючи одержану систему рівнянь відносно та , одержимо:

;

.

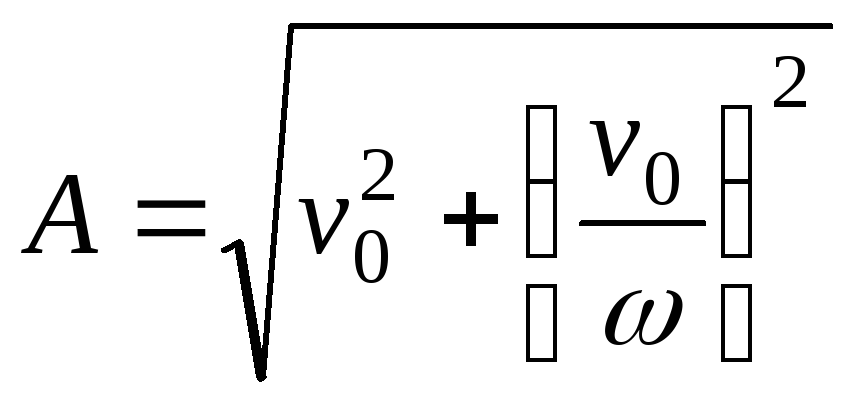Графік зміни переміщення протягом часу показаний на рис.16.5.

Найбільше відхилення від стану рівноваги в той або інший бік буде тоді, коли дорівнює одиниці. Як видно з рівняння (16.6), воно дорівнюватиме параметру . Таким чином, величина є амплітудою коливань. Час , за який відбувається один повний цикл коливань, називається періодом коливань. Через кожні секунд відхилення набуває колишнього значення.

З рівняння (16.6) маємо:

.

Отже,

,

звідки колова частота власних коливань, яка є числом коливань за секунд, дорівнює:

.

Рис.16.5

Колову частоту власних коливань відповідно до прийнятого вище позначення можна визначити за формулою:

, (16.8)

де  статичний прогин того перерізу, у якому прикладена зосереджена маса , що коливається, викликаний дією відповідної статично прикладеної сили тяжіння .

В теоретичній механіці частоту власних коливань визначають за допомогою жорсткості системи. Жорсткістю системи при коливаннях називається сила, яку потрібно прикласти в тому перерізі, де знаходиться маса, що коливається, щоб викликати переміщення цього перерізу, що дорівнює одиниці.

Якщо  одиничне переміщення, то величина їй зворотна є жорсткість системи при коливаннях.

Перетворюючи вираз (16.8), одержимо:

. (16.9)

Формула (16.9) для колової частоти власних коливань є класичною формулою теоретичної механіки.

При необхідності урахування власної ваги тіла при визначенні колової частоти власних коливань в перерізі, у якому прикладена зосереджена маса, що коливається, слід додатково прикласти зведену масу тіла , де  розподілена маса уздовж тіла;  коефіцієнт зведення маси (вага), описаний в попередній темі, де коефіцієнт використовувався при обчисленні динамічного коефіцієнта при ударі. Тоді формула (16.8) для визначення колової частоти власних коливань перетвориться до вигляду:

. (16.10)

У деяких випадках для скорочення часу обчислень корисно запам'ятати значення жорсткості системи для деяких найпоширеніших випадків навантаження стержнів, балок, валів та пружин.

Таблица 16.1

Вид системи	Жорсткість системи	Частота власних коливань

У таблиці 16.1 наведені для деяких таких випадків навантаження вирази для жорсткості і частоти власних коливань.

Для скручуваного валу при обчисленні колової частоти власний коливань слід використовувати момент інерції диска відносно осі стержня, перпендикулярної до площини диска .

Обчислимо період і колову частоту власних коливань для системи з двома дисками, що обертаються (Рис.16.6) [3].

Якщо закрутити диски один відносно іншого, а потім миттєво зняти прикладені зовнішні моменти, то диски почнуть здійснювати крутильні коливання назустріч один одному. При цьому деякий проміжний переріз вала залишатиметься нерухомим.

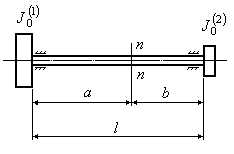
Рис.16.6

Положення цього так званого вузлового перерізу можна знайти з умови рівності частот коливань обох дисків з примикаючими до них ділянками валу завдовжки і , для яких застосовані формули:

,

звідки

,

де і  моменти інерції відповідно першого і другого дисків.

Використовуючи останнє співвідношення, а також, беручи до уваги, що , знаходимо:

; .

Тоді період і частота крутильних коливань системи будуть такими:

; .

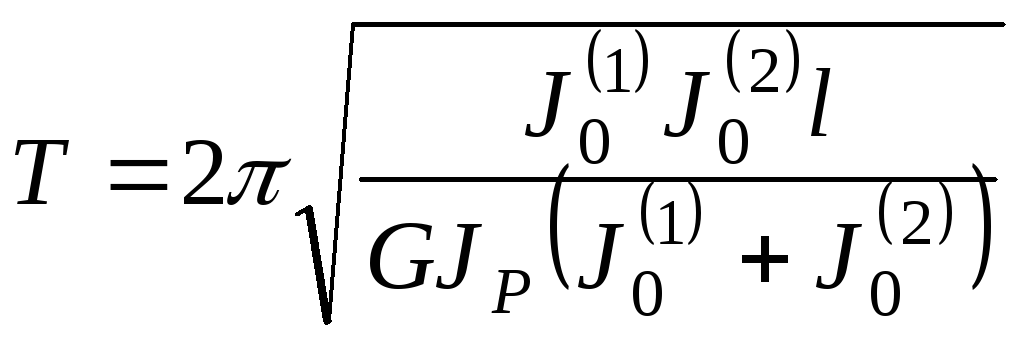Розглянемо приклади обчислення кругової частоти власних коливань.

Приклад 16.1. Визначити частоту власних коливань вантажу вагою Н, підвішеного до кінця сталевого стержня завдовжки м і площею поперечного перерізу см², якщо модуль пружності матеріалу МПа.

Розв’язок:

1. Обчислимо подовження стержня:

м.

2. Визначаємо частоту власних коливань за формулою:

с^–1.

Приклад 16.2. Знайти період власних коливань кручення сталевого валу діаметром см і довжиною м, один кінець якого затиснений, а на другому насаджений шків з моментом інерції Нмс².

Розв’язок:

1. Визначаємо колову частоту власних крутильних коливань, скориставшися формулою з таблиці 16.1:

с^–1.

2. Знаходимо період власних крутильних коливань валу:

с.

Приклад 16.3. Сталева циліндрична пружина, яка має витків при середньому діаметрі витка см і діаметрі дроту мм, розтягнута вантажем Н. Визначити частоту власних коливань вантажу.

Розв’язок:

1. Обчислюємо жорсткість пружини:

Н/м.

2. Визначаємо частоту власних коливань:

с^–1.

Приклад 16.4. Двотаврова балка №27 довжиною м, шарнірно закріплена на кінцях, несе посередині прольоту вантаж кН. Момент інерції двотавру см⁴, вага одного погонного метра Н/м. Коефіцієнт зведення ваги прийняти . Визначити частоту власних коливань без урахування і з урахуванням маси балки.

Розв’язок:

1. Визначаємо жорсткість балки:

Н/м.

2. Знаходимо частоту власних коливань без урахування власної ваги балки:

с^–1.

3. Визначаємо частоту власних коливань з урахуванням власної ваги балки:

с^–1.

Приклад 16.5. Визначити частоту власних коливань для двотаврової балки №27 з моментом інерції см⁴, якщо вантаж кН прикладений на відстані м від лівої опори (Рис.16.7,а). Довжина балки м. Власною вагою балки нехтувати.

Рис.16.7

Розв’язок:

1. Знайдемо статичне переміщення (прогин) перерізу С, в якому прикладений вантаж . Для цього спочатку побудуємо епюру вантажних моментів (Рис.16.7,б). Згинальний момент в перерізі С визначимо за допомогою формули:

кНм.

Потім виберемо одиничний стан балки (Рис.16.7,в), прикладемо в перерізі С одиничну зосереджену силу і побудуємо епюру одиничних згинальних моментів (Рис.16.7,г). Згинальний момент в перерізі С знайдемо за формулою:

.

Використовуючи формулу трикутників, знайдемо статичний прогин в перерізі С:

м.

2. Визначаємо частоту власних коливань балки:

с^–1.

16.3. Урахування сил внутрішнього опору при визначенні частоти власних коливань

Наведений вище спосіб визначення частоти власних коливання є наближеним, оскільки він не враховує сили опору, наприклад, опір повітря, сили тертя в шарнірах, сили внутрішнього опору.

Сили опору повітря при швидкостях коливань, які спостерігаються в балках, незначні і тому їх можна не враховувати. Сили тертя в шарнірах можуть бути усунені або зведені до мінімуму за рахунок поліпшення конструкцій шарнірних опор або їх змащування.

Основними є сили внутрішнього непружного опору, які залежать від матеріалу балки і ряду інших чинників. Ці сили усунути неможливо.

За однією з найпоширеніших гіпотез урахування загасань, запропонованих Фойгтом [6], матеріал розглядається як в'язко-пружне тіло, у якому виникаючі напруження залежать не тільки від величини деформації , але і від швидкості зміни деформації протягом часу:

, (16.11)

де  коефіцієнт в'язкого тертя.

У відповідності до гіпотези Фойгта ефект сил внутрішнього опору при коливаннях даної балки замінюється дією зовнішньої сили , прикладеної в точці закріплення маси, де  коефіцієнт пропорційності між силою і швидкістю.

Величина відхилення маси від стану рівноваги з урахуванням сил внутрішнього опору має вигляд:

,

звідки

, (16.12)

де

; .

Вираз (16.12) є диференціальним рівнянням власних коливань системи з одним ступенем вільності з урахуванням непружних сил опору. Інтеграл рівняння (16.12) можна записати у вигляді:

, (16.13)

де

. (16.14)

З графіка коливань (Рис.16.8), побудованого за виразом (16.13), добре видно, що власні коливання швидко затухають.

Рис.16.8

Вираз (16.14) дає значення частоти власних коливань з урахуванням сил опору. Величина зазвичай мала у порівнянні з , тому і мало відрізняються одне від одного:

.

Щоб оцінити швидкість загасання коливального процесу, складемо відношення двох відхилень маси, заміряних через один період (Рис.16.8):

,

звідки

. (16.15)

Величину називають логарифмічним декрементом коливань, він характеризує швидкість загасання власних коливань.