Лабораторна робота № 4

Тема: «Середні статистичні величини та показники варіації»

Мета роботи – поглиблення теоретичних знань й набуття практичних навичок щодо реалізації вихідного співвідношення середньої, обґрунтування вибору та розрахунку видів і форм середніх величин, визначення щільності розподілу, абсолютних і відносних показників варіації, способів розрахунку структурних характеристик варіаційного ряду

Час виконання роботи – 4 години

Методичні вказівки до виконання завдань 4.1-4.3

Для обґрунтування вибору форми та виду середньої, насамперед, необхідно визначити характер вихідного матеріалу, тобто: що буде ознакою (усереднюванню величиною) , а що (частотою) При визначенні середньої величини за формулами арифметичної та гармонійної використовується тільки необхідна вихідна інформація.

Найбільш розповсюдженим видом середніх величин є середня арифметична, котра, як і всі середні, у залежності від характеру наявних даних, буває двох видів:

• проста:

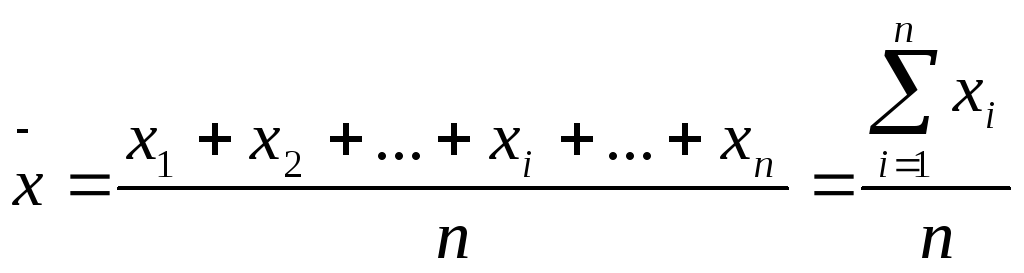, (4.1)

де ‑  значення ознаки (варіанти);

‑кількість варіантів.

• зважена

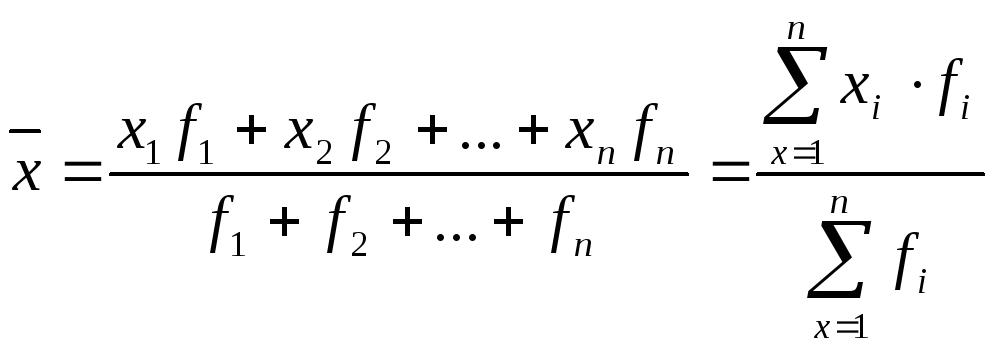(4.2)

Якщо замість частот у процесі обчислення середньої за даними ряду розподілу використовуються частки 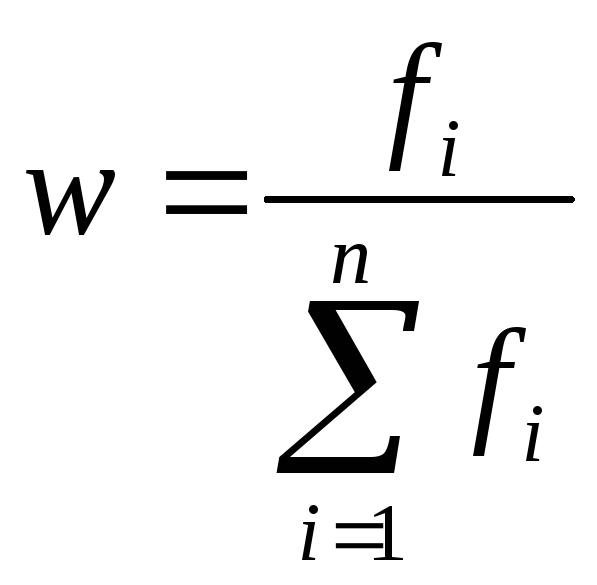, то формула середньої арифметичної зваженої набуває вигляду:

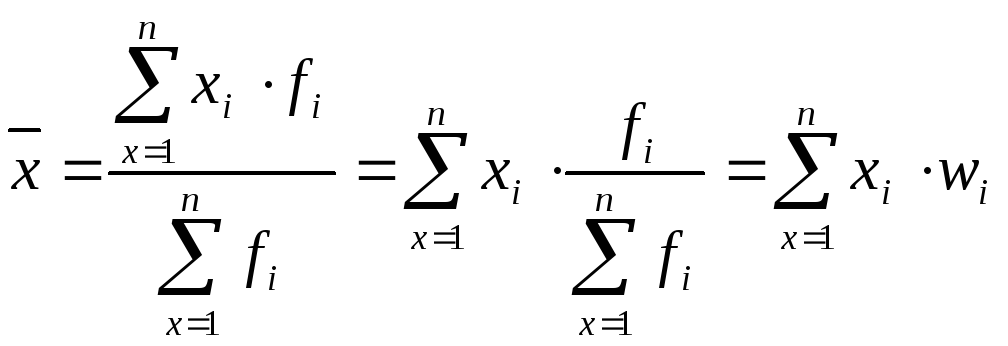(4.3)

Досить часто розрахунок середньої здійснюється за даними інтервальних рядів розподілу, коли варіанти ознаки подаються у вигляді інтервалу (від... до). Тому для обчислення середньої спочатку потрібно перетворити інтервальний ряд на дискретний, для чого в кожній групі визначають середнє значення інтервалу.

Середнє значення інтервалу знаходять як напівсуму його верхньої та нижньої межі. Середнє значення відкритого інтервалу визначають з величини інтервалу наступної групи або попередньої. Після визначення середнього значення інтервалів, подальші розрахунки здійснюють так само, як і дискретному варіаційному ряду: варіанти перемножуються на частоти і суму добутків ділять на суму частот.

Середня гармонійна зважена застосовується в тих випадках, коли відомі індивідуальні значення ознаки та їх добутки на частоти, значення ж частот невідомі. Як і середня арифметична, середня гармонійна може бути проста і зважена.

Формула середньої гармонійної простої має такий вигляд:

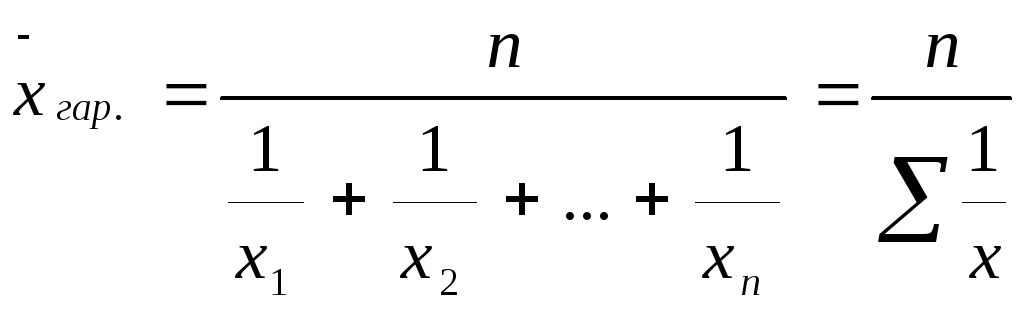, (4.4)

де сума обернених значень варіант;

‑число варіант.

Таким чином, середня гармонійна – це величина, обернена середній арифметичній із обернених значень ознаки. Вона використовується в тому випадку, коли обсяг явищ, тобто добутки за кожною ознакою рівні.

Середня гармонійна зважена має вигляд:

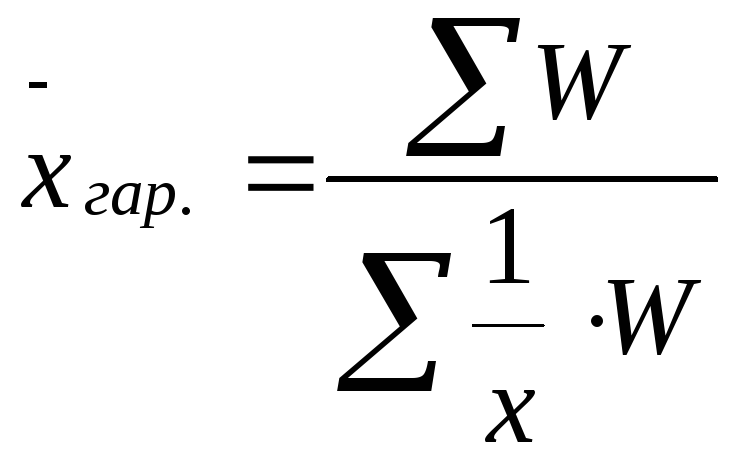, (4.5)

оскільки,

де W ‑ добуток варіант на частоти;

‑обернені значення варіантів.

Вона використовується в тому випадку, коли обсяг явищ, тобто добутки ознаки на частоту за кожною ознакою нерівні.

Для аналізу рядів динаміки, зокрема, при визначенні середнього темпу росту, застосовують середню геометричну. При визначенні середнього темпу росту динамічного ряду з рівними проміжками часу використовують формулу середньої геометричної простої:

, (4.6)

де К ‑ змінні коефіцієнти росту;

n ‑ число змінних коефіцієнтів росту.

Для розрахунку можна використовувати абсолютні рівні ряду:

, (4.7)

де у₀ та у_n ‑  відповідно початковий та останній рівні ряду.

Темп приросту Т_пр. показує на скільки % порівнюваний рівень більший або менший від рівня, взятого за базу порівняння, тобто:

(4.8)

Для розрахунку середнього рівня моментного ряду використовують середню хронологічну. Середньою хронологічною називають середню, обчислену із значень, які змінюються в часі. Розрізняють середню хронологічну просту і зважену.

Середня хронологічна проста застосовується для визначення середнього значення моментного ряду з рівними інтервалами часу і має вигляд:

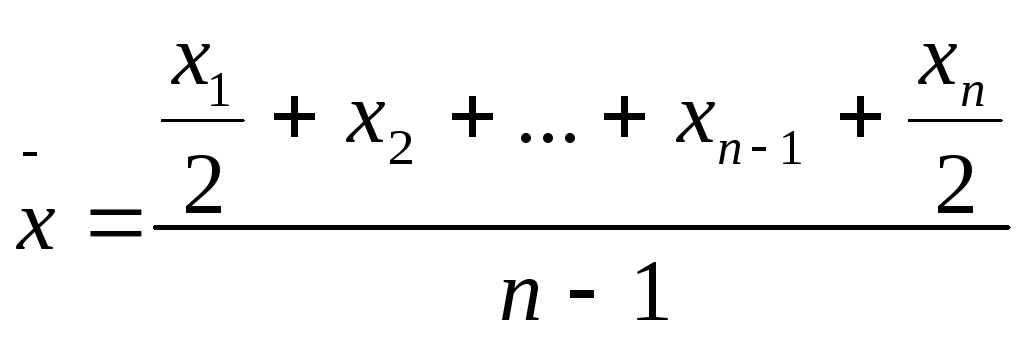(4.9)

Середня хронологічна зважена застосовується для визначення середнього значення моментного ряду з нерівними інтервалами часу й обчислюється за формулою:

, (4.10)

де х₁......х_n ‑ рівні ряду динаміки;

t ‑ тривалість терміну часу між рівнями.

В інтервальних рядах розподілу з рівними інтервалами частоти і частки дають уявлення про ступінь заповнення їх одиницями сукупності та можливість їх порівнювати. В інтервальних рядах з нерівними інтервалами такого порівняння здійснювати не можна, тому визначають показник, який називається щільністю інтервалів або розподілу.

Щільність розподілу ()показує, скільки одиниць сукупності або який їх відсоток припадає в середньому на одиницю величини інтервалу групувальної ознаки.

Вона визначається діленням частоти або частки (або) відповідного інтервалу на його величину (). Розрізняють:

• абсолютну щільність:

(4.11)

• відносну щільність:

(4.12)

Для статистичного вивчення рядів розподілу використовують наступні характеристики центру розподілу:

• середня;

• мода;

• медіана.

На відміну від середньої для більш глибинного розкриття властивостей ряду розподілу обчислюють особливі показники, які у статистиці називають структурними середніми величинами. Це мода й медіана, які є допоміжними описовими характеристиками розподілу варіаційної ознаки.

Мода (Мо) – це величина ознаки (варіанта), яка найчастіше зустрічається у даній сукупності. У варіаційному ряду це – варіант, що має найбільшу частоту.

Медіаною (М_е) в статистиці називають варіант, що знаходиться посередині упорядкованого (ранжованого) варіаційного ряду, тобто ділить його на дві рівні частини: одна частина має значення варіюючої ознаки менше між середня, а друга – більше. Медіана показує величину варіюючої ознаки, якої досягла половина одиниць сукупності.

На відміну від дискретних в інтервальних варіаційних рядах визначення моди і медіани має певні особливості. Мода визначається в наступній послідовності: спочатку необхідно визначити модальний інтервал, якому відповідає найбільша частота або частка, а значення моди в інтервальному ряду обчислюється за формулою Орженцького:

, (4.13)

де ‑ нижня межа модального інтервалу;

‑величина модального інтервалу;

‑частота модального інтервалу;

‑частота інтервалу, що передує модальному;

‑частота інтервалу, що йде за модальним.

Для визначення медіани необхідно знайти медіанний інтервал, кумулятивна частота якого дорівнює або перевищує половину суми частот. Кумулятивна частота визначається шляхом поступового додавання частот, починаючи з інтервалу, який має найменше значення ознаки.

Значення медіани обчислюють за формулою Фехнера:

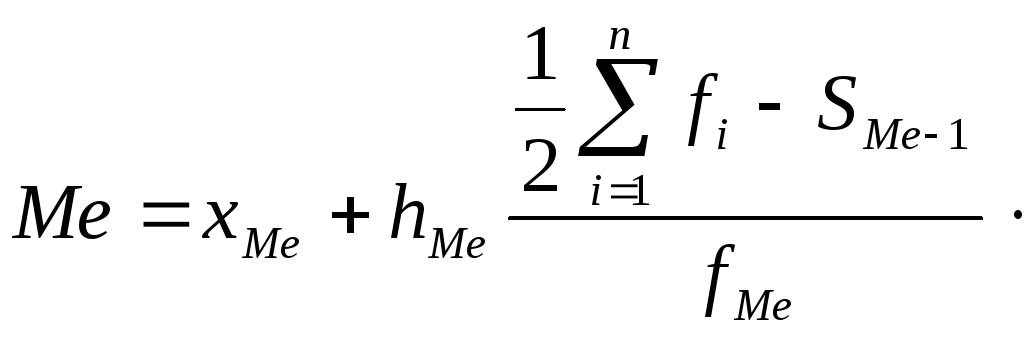, (4.14)

де ‑ нижня межа медіанного інтервалу;

‑величина медіанного інтервалу;

‑сума частот ряду;

‑сума накопичених частот передмедіанного інтервалу;

‑частота медіанного інтервалу.

Відмінність індивідуальних значень ознаки всередині досліджуваної сукупності в статистиці називається варіацією ознаки. Для вивчення варіації розроблена система абсолютних та відносних показників.

До абсолютних показників, за допомогою яких вимірюють відхилення від середньої, належать:

• розмах варіації;

• середнє лінійне (арифметичне) відхилення;

• дисперсія;

• середнє квадратичне) відхилення;

Розмах варіації R є найпростішим абсолютним показником у системі показників варіації, що характеризує межі, в яких змінюється значення ознаки й визначається як різниця між найбільшим (х_max) та найменшим (х_min) значеннями ознаки:

(4.15)

В інтервальному ряду розподілу розмах варіації визначають як різницю між верхньою межею останнього інтервалу і нижньою межею першого або як різницю між середніми значеннями цих інтервалів.

Іншою характеристикою варіації ознаки є середнє арифметичне або лінійне відхилення, яке визначається як середнє арифметичне з абсолютних відхилень індивідуальних значень ознаки від їх середньої величини.

Пам’ятаючи що, суму відхилень беруть за модулем, тобто без урахування знаку відхилення. Формула середнього лінійного відхилення має вигляд:

• для незгрупованих даних: 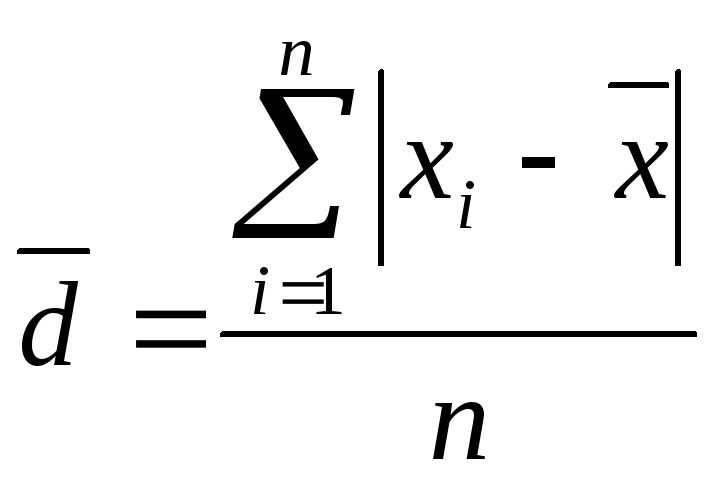; (4.16)

• для згрупованих даних: 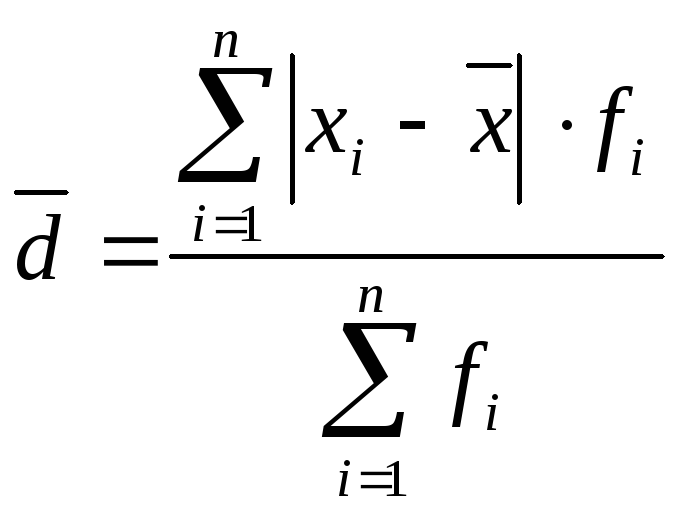; (4.17)

Середнє лінійне відхилення відображає абсолютні розміри варіації досліджуваної ознаки на основі всіх її значень. Однак цей показник варіації не враховує знаків відхилень.

Щоб усунути цей недолік, відхилення значень ознаки від їх середнього значення підносять до квадрату й обчислюють показник варіації, який називають дисперсією.

Дисперсія () являє собою середню арифметичну з суми квадратів відхилень окремих значень ознаки від їх середньої й обчислюється за формулою:

• для незгрупованих даних: ; (4.18)

• для згрупованих даних: 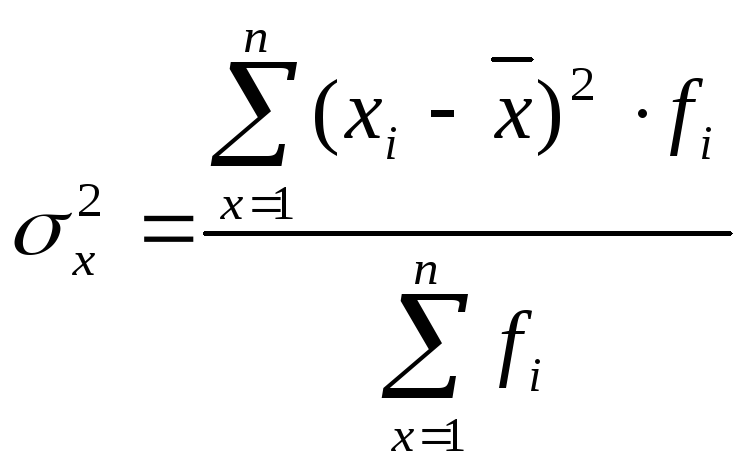. (4.19)

На практиці застосовують спрощений метод визначення дисперсії за формулою: дисперсія ознаки дорівнює різниці між середнім квадратом значень ознаки і квадратом її середньої:

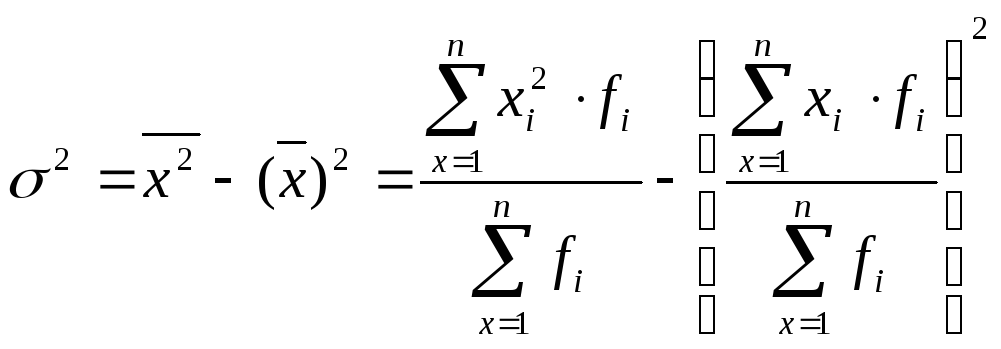(4.20)

Недолік дисперсії в тому, що вона має одиниці вимірювання, які позбавлені економічного змісту , тому дисперсія зазвичай записується без одиниць вимірювання.

Корінь квадратний із середнього квадрату відхилень варіантів від їх середньої (тобто дисперсії) називається середні квадратичним відхиленням й визначається за формулою:

• для незгрупованих даних: 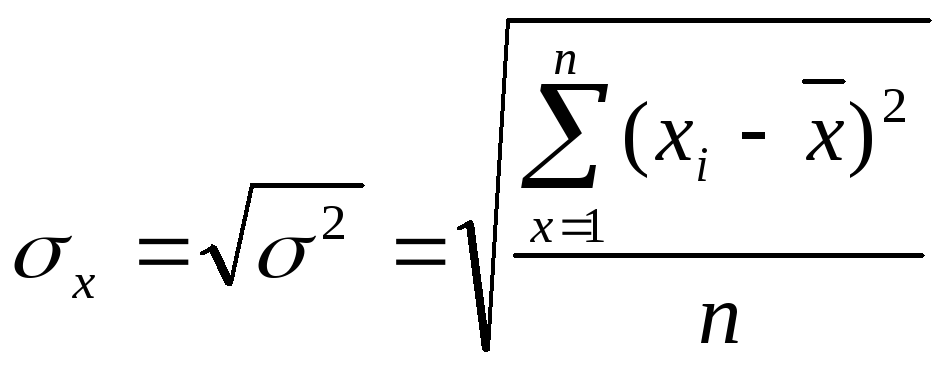; (4.21)

• для згрупованих даних: 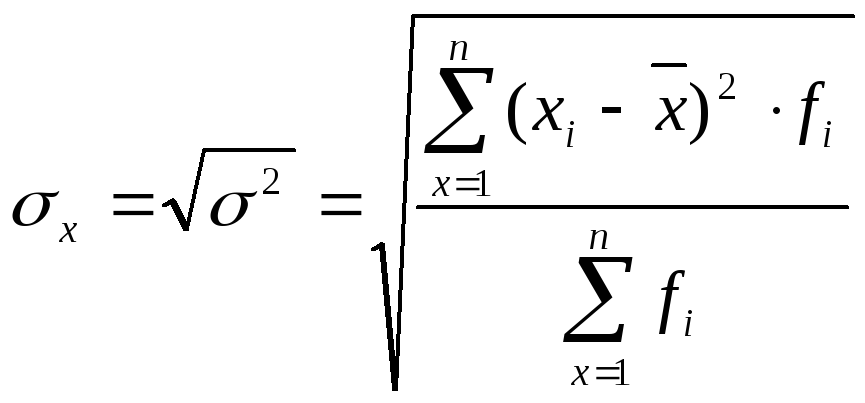 (4.22)

Середнє квадратичне відхилення завжди виражається в тих же одиницях, що й ознака, і є абсолютною мірою варіації. Чим менше середнє квадратичне відхилення, тим типовіша середня і тим більш однорідна сукупність.

Усі розглянуті показники варіації характеризують абсолютний розмір варіації й виражаються в одиницях вимірювання досліджуваної ознаки, тому вони не придатні для порівняння ступеня варіації різних ознак. Для порівняння варіації різних ознак в одній сукупності або однієї ознаки в кількох сукупностях з різною середньою величиною використовують відносні показники варіації – коефіцієнти варіації.

Розраховують наступні коефіцієнти варіації:

1) коефіцієнт осциляції, який відображає відносну коливніть крайніх значень ознаки навколо середньої:

(4.23)

2) лінійний коефіцієнт варіації характеризує частку усередненого значення абсолютних відхилень від середньої величини (відносне лінійне відхилення):

(4.24)