
Higher_Mathematics_Part_2
.pdf
19. |
Find ∫ |
|
|
|
dx |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1+ 9x |
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|||||
Solution. ∫ |
|
|
dx |
|
|
|
= |
1 |
∫ |
|
dx |
|
= |
1 |
∫ |
|
|
= |
1 |
arctg 3x + C . |
||||||
1 |
+ 9x |
2 |
|
9 |
1/ 9 |
+ x |
2 |
9 |
(1/ 3) |
2 |
+ x |
2 |
3 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
20. |
Find ∫ |
|
|
x 2 dx |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
x |
+ 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Solution. As the power of the numerator is not less than that of the
denominator, we use long division: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x 2 dx |
|
|
|
|
|
|
|
(x 2 |
+ 1) − 1 |
dx |
|
|
|
|
|
|
|
|
1 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
= |
|
1− |
|
|
|
|
|
|
dx = |
|
|
|||||
|
|
|
|
|
|
∫ x 2 |
|
|
|
|
|
∫ x 2 + 1 |
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
+ 1 |
|
|
|
|
|
|
|
|
|
|
|
x2 + 1 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∫ dx − ∫ |
|
|
dx |
|
|
= x − arctg x + C . |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
21. Find ∫ |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5x + 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Solution. ∫ |
|
|
dx |
|
= |
|
1 |
ln | 5x + 3 | +C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
5x + 3 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
22. Find ∫cos3xdx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Solution. ∫cos 3xdx = |
1 |
sin 3x + C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
23. Find ∫(2x − 1)5 dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Solution. ∫(2x − 1)5 dx = |
1 (2x − 1)6 |
|
+ C = |
(2x − 1)6 |
+ C . |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
24. Find ∫ |
|
|
|
xdx |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x + 2 |
|
|
|
|
(x + 2) − 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Solution. ∫ |
xdx |
= |
∫ |
dx = |
|
∫ dx − 2∫ |
dx |
= |
|
|
|
|
||||||||||||||||||||||||||||||||
x + 2 |
|
|
|
|
|
|
x + 2 |
|
x + 2 |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
= x −2 ln |
|
x +2 |
|
+C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
25. Find ∫ |
|
|
|
|
|
5dx |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
5 − (3x |
+ 8)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Solution. By formula 13 and (2.1): ∫ |
|
|
|
|
|
5dx |
|
|
|
= |
5 |
arcsin |
3x + 8 |
+ C. |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 − (3x + 8)2 |
3 |
|
|
5 |
|
|||||||||||
26. Find ∫ |
|
|
|
|
4dx |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4x |
2 |
− 6x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
+ 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
71 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

Solution. First perform algebraic manipulations on an integrand, as is shown:
|
|
|
|
|
|
|
|
4x |
2 |
– 6x + 7 |
|
2x − |
3 |
|
2 |
19 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
= |
|
|
|
+ |
|
|
|
. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2 |
4 |
|
|
|
|||||||||||||
Now it is easy to find the integral: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
4dx |
|
|
1 2 |
|
|
2x − |
3 |
|
|
|
|
|
4 |
|
4x − 3 |
|
|||||||
∫ |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
= 4 |
|
|
|
arctg |
|
|
|
|
|
+ C |
= |
|
|
arctg |
|
+ C. |
||||
|
2x − |
3 |
2 |
+ |
19 |
2 |
19 |
19 |
|
|
|
19 |
19 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ІІ. Using substitution
27. Find ∫ |
2xdx |
|
|
|
|
|
|
|
|
|
|
|||
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
x2 + 7 |
|
|
|
|
|
|
|
|
|
|
||||
Solution. Note that 2x is the derivative of x2 + 7. Introduce u = x2+7. Then |
||||||||||||||
|
|
2xdx |
|
du |
|
|
|
|
|
|
||||
du = 2xdx, and ∫ |
|
= ∫ u . |
|
|
|
|
|
|
||||||
x2 + 7 |
|
|
|
|
|
|
||||||||
Now it’s easy to find |
∫ duu . |
|
|
yields ln|x2 + 7|. Since x2 + 7 is always |
||||||||||
Replacing u by x2 + 7 in ln|u| |
|
|
||||||||||||
positive we can omit the absolute-value bars: |
|
|
||||||||||||
|
|
|
|
|
|
∫ |
2xdx |
|
= ln (x |
2 |
+ 7)+ C. |
|||
|
|
|
|
|
|
x2 + 7 |
|
|
||||||
|
|
|
|
|
|
2xdx |
|
d |
x2 + 7 |
) |
|
|||
We can write this as |
∫ |
= ∫ |
|
|
( |
= ln (x2 + 7)+ C. |
||||||||
x2 + 7 |
|
|
x2 + 7 |
|
||||||||||
28. Find ∫ x 2 − xdx .
2 − xdx .
Solution. Using the substitution |
|
2 − x = t , we get |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
2 − x = t 2 , |
x = 2 − t 2 |
and |
dx = −2tdt . |
|
|
|
|
|
|
||||
Then evaluate the new indefinite integral: |
|
2 |
|
|
4 |
|
|
|
|
|||||||||
∫ x 2 − xdx = ∫(2 − t 2 ) t (−2t)dt = 2∫(t |
4 − 2t 2 )dt = |
t 5 |
− |
t 3 |
+ C . |
|||||||||||||
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
5 |
|
3 |
|
|
|
|
|||
Replacing t by |
2 − x we have |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
∫ x |
|
2 − xdx = 2 |
(2 − x)5 |
− 4 |
(2 − x)3 + C . |
|
|
|
|
|
|
||||
|
|
|
|
5 |
|
|
3 |
|
|
|
|
|
|
|
|
|
||
29. Find ∫ |
|
|
dx |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
− e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Solution. Using the substitution |
1− e x |
= t . In this case it’s more useful to |
||||||||||||||||
find dt : dt = −e x dx |
|
and just as − e x |
= t − 1 so dt = (t − 1)dx , or |
dx = |
|
dt |
. |
|||||||||||
|
t |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 1 |
|||
|
|
|
|
|
|
|
72 |
|
|
|
|
|
|
|
|
|
|
|
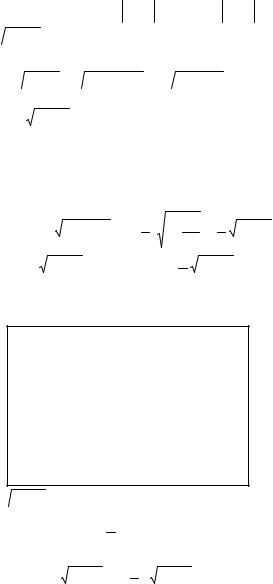
Since
∫ |
|
|
dx |
|
= ∫ |
dt |
= ∫ |
t − (t − 1) |
|
1 |
|
|
1 |
|
d (t − 1) |
|
dt |
|
||
|
|
|
|
|
|
dt = ∫ |
|
|
− |
|
|
|
dt = ∫ |
|
− ∫ |
|
= |
|||
1 |
− e |
x |
t(t − 1) |
t(t − 1) |
|
|
|
t |
t − 1 |
t |
||||||||||
|
|
|
|
t − 1 |
|
|
|
|
|
|||||||||||
= ln | t − 1| − ln | t | +C = ln ex − ln 1− ex + C = x − ln1− e x + C .
30. Find ∫  4 − x 2 dx .
4 − x 2 dx .
Solution. Using the substitution x = 2 sin t , dx = 2 cos tdt . Thereby
 4 − x 2 =
4 − x 2 =  4 − 4 sin 2 t = 2
4 − 4 sin 2 t = 2 1− sin 2 t = 2 cos t .
1− sin 2 t = 2 cos t .
Therefore
∫ 4 − x 2 dx = ∫ 2 cos t 2 cos tdt = 4∫cos2 tdt = |
|||||||||||
= 2∫(1+ cos 2t)dt = 2t + sin 2t + C . |
|||||||||||
Replacing t, we have: |
|
|
|
|
|
|
|
|
|||
sin t = |
x |
, t = arcsin |
x |
, |
|
sin 2t = 2 sin t cos t = |
|||||
|
|
||||||||||
2 |
|
2 |
|
|
|
|
|
|
|||
= 2 sin t 1− sin 2 t |
= 2 |
x |
|
1− x 2 |
= x |
4 − x 2 , |
|||||
|
|
|
|
|
2 |
|
|
4 |
2 |
|
|
∫ 4 − x 2 dx = 2 arcsin |
|
x |
+ x |
4 − x 2 |
+ C . |
||||||
2 |
|||||||||||
|
|
|
|
|
|
2 |
|
|
|||
Frequently the basic integration form (2.2) is useful. It is provided to perform the following algebraic manipulations of the differential.
dx = d(x + b) , b is a constant,
dx = |
1 |
|
d (ax + b) , |
а, b are the constants, |
||||||
|
|
|||||||||
|
a |
|
|
|
|
|
||||
xdx = |
1 |
d (x2 ) , |
|
dx |
= d(ln x) , |
|||||
|
2 |
|
|
x |
|
|
||||
cos xdx = d (sin x) , |
sin xdx = −d (cos x) , |
|||||||||
dx |
|
|
|
= d (tg x) , |
|
dx |
|
= −d (ctg x) |
||
cos2 |
|
|
|
|
sin2 |
|
||||
x |
|
x |
||||||||
31. Find ∫ x 1 + x2 dx .
1 + x2 dx .
Solution. As in our case xdx = 12 d (1 + x2 ) , for the original integral we can
state
∫ x 1 + x2 dx = 12 ∫ 1 + x2 d (1 + x2 ) .
73

|
|
|
|
|
1 |
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
The table integral is provided ∫u 2 dx = |
|
u 2 + C , we get |
|
|||||||||||||||||||||||||||
3 |
|
|||||||||||||||||||||||||||||
|
|
∫ x 1 + x2 dx = |
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
∫(1 + x2 ) |
|
d (1 + x2 ) = |
||||||||||||||||||||||||||
|
|
2 |
||||||||||||||||||||||||||||
|
|
2 |
||||||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
||||||||||||||||
|
|
= |
1 |
|
2 |
(1 + x2 ) |
|
|
+ C = |
1 |
(1 + x2 ) |
|
|
|
+ C . |
|||||||||||||||
|
|
2 |
2 |
|
||||||||||||||||||||||||||
|
|
|
3 |
3 |
||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
32. Find ∫ x3e− x4 dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||
Solution. Finding d(− x4 ) = −4x3dx , then |
x3dx = − |
d (− x4 ) . Hence |
||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
||||||||||
|
∫ x3e− x4 dx = − |
∫e− x4 d(− x 4 ) = − |
1 |
e− x4 |
+ C . |
|||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
|
dx |
4 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
||||||||||||
33. Find ∫ |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x 1 |
− ln 2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Solution. As in our case d(ln x) = |
1 |
dx , for the original integral we can state |
|||||||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
dx |
x |
d ln x . |
|||
|
|
|
|
|
∫ |
|
|
= ∫ |
|||||
|
|
|
|
|
|
|
x 1 − ln 2 x |
1 − ln 2 x |
|||||
We get the table integral ∫ |
du |
|
= arcsin u + C . Therefore, |
||||||||||
|
|
|
|
|
|
|
|
1 − u 2 |
|
|
|
||
|
|
|
|
|
|
|
|
dx |
|
= arcsin(ln x) + C . |
|||
|
|
|
|
|
∫ x |
|
|
|
|||||
|
|
arctg x |
|
|
1− ln2 x |
|
|
|
|||||
34. Find ∫ |
dx . |
|
|
|
|
|
|
|
|||||
2 |
|
|
|
|
|
|
|
||||||
|
|
1+ x |
|
|
|
|
|
arctg2 x |
|
||||
Solution. |
∫ |
arctg x |
dx = ∫ arctg xd (arctg x) = |
+ C . |
|||||||||
2 |
|
||||||||||||
|
|
|
1+ x |
|
|
|
|
2 |
|
||||
35. Find |
∫ x2 x3 − 7dx . |
|
|
|
|
|
|
||||||
1
Solution. We can write this as ∫ x2 (x3 −7)2 dx . Notice that the integrand
contains a power of the function x3 – 7. If u = x3 – 7 then du = 3x2dx.
Since the constant factor is 3 in du, the constant 7 does not appear in the integrand, this integral does not have the form of ∫un du . However we can put
the given integral in this form by first multiplying and dividing it by 3. This does not change the value. Thus:
74

|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
u = x3 − 7 |
|
||||||||||
|
|
∫ x2 x3 − 7dx = |
∫(x3 − 7)2 3x2dx = |
|
|
|
|
|
|
= |
|||||||||||||||||||||
|
|
3 |
du = 3x2dx |
||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
||
|
|
1 |
|
|
|
1 |
|
u 2 |
|
|
|
2 |
|
|
|
2 |
|
|
3 |
|
|
||||||||||
= |
∫u 2 du |
= |
|
|
+ C = |
u 2 |
+ C = |
|
(x |
− 7)2 |
+ C. |
||||||||||||||||||||
3 |
|
3 |
3 |
|
|
3 3 |
9 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||
Or ∫ x2 x3 − 7dx = |
1 |
∫ |
|
|
x3 − 7d (x3 − 7)= |
2 |
(x3 − 7) |
|
+ C. |
|
|||||||||||||||||||||
|
2 |
|
|||||||||||||||||||||||||||||
3 |
|
9 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
36. Find ∫ |
|
4x3 − 3x |
|
|
dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2x |
4 |
− 3x |
2 |
+ |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Solution.
If u = 2x4– 3x2 + 7 then du = (8x3 – 6x)dx which is two times greater then the numerator.
We multiply the integrand by 2 and compensate it by the factor 12 putting it before the integral sign.
|
1 2(4x3 − 3x)dx 1 |
|
|
|
|
|
|
(8x3 − 6x)dx |
|
|
|
u = 2x4 − 3x2 + 7 |
|
1 du |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
∫ |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
= |
|
du = (8x3 − 6x)dx |
= |
|
∫ |
|
|
= |
|||||||||||||||||||||||
2 |
2x4 − 3x2 + 7 |
2 |
2x4 − 3x2 + 7 |
2 |
u |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
1 |
ln |
|
|
|
|
|
+ C = |
1 |
|
ln |
|
2x4 |
|
− 3x2 + 7 |
|
+ C. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
37. |
Find |
∫ |
|
sin xdx |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
2 + cos2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Solution. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
∫ |
|
|
sin xdx |
|
= |
|
t = cos x |
|
= −∫ |
(− sin x)dx |
|
= |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
= −∫ |
|
dt |
2 + cos x |
|
|
|
|
|
|
|
|
dt = − sin xdx |
|
|
|
|
|
|
2 + cos2 x |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
= − ln |
|
t + 2 + t2 |
|
+ C = − ln |
|
cos x + 2 + cos2 x |
|
+ C. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 + t2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
38. |
Find |
∫ |
2dx |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x ln |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Solution. |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
2dx |
|
|
|
t = ln x |
|
|
|
dt |
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
∫ |
|
|
= |
dt = |
dx |
|
|
= |
2∫ |
|
|
|
= 2∫t−3dt = − |
|
t−2 + C = C |
− |
|
. |
|||||||||||||||||||||||||||||||||||||||
|
|
|
x ln3 x |
t3 |
|
2 |
ln2 x |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
75 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

ІІІ. Using integration by parts
39. Find |
∫ x cos xdx . |
Solution. |
To use the formula (2.1), it is necessary to write ∫ x cos xdx in the |
form ∫udu . The integrand is so simple that there is not much choice. Try u = x and dv = cos x dx; that is break up the integrand this way:
∫x cosx dx u dv
Then find du and v. Since u = x, it follows that du = dx. Since dv = cos x dx, we choose v = sin x. Of course v could be sin x + C for any constant C, but choose the simplest v whose derivative is cos x. Applying integration by parts yields:
∫ x cos x dx = x sin x − ∫ sinx dx.
u dv |
u v |
v du |
∫v du is simpler than the original integral ∫u dv.
∫ sin x dx = −cos x − C.
Hence ∫ x cos x dx = x sinx + cosx + C. Save the constant of integration till the end. The reader may check this by differentiation.
We denote: u = cos x; dv = x dx. Let us see what this method gives:
∫ x cos xdx = |
|
u = cos x du = − sin xdx |
|
= − |
x2 cos x |
+ ∫ |
x2 |
sin xdx. |
||
|
|
|||||||||
|
|
x2 |
|
|||||||
|
dv = xdx v = |
|
|
|
||||||
|
|
|
|
|
2 |
2 |
|
|||
|
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
||
The new integrand is harder than the one we started with. Though sinx is not
harder than cosx; x2 sin x is definitely harder than xcosx for the exponent has 2
increased from 1 to 2. 40. Find ∫ x ln xdx.
Solution.
Setting dv = lnxdx is not a wise move since v = ∫ln xdx is not immediately
apparent. But setting u = lnx is promising since du = dxx is much easier than lnx. This second approach goes through smoothly:
76
|
|
u = ln x du = |
dx |
|
|
x2 |
|
|
|
x2 |
|
dx |
|
||||||||
∫ x ln xdx = |
|
x2 |
|
= |
|
− ∫ |
|
= |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||||||||
|
|
dv = xdx v = |
|
x |
|
2 |
|
|
2 |
|
|
||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= |
x2 ln x |
− |
1 |
∫ xdx = |
x2 |
|
ln x − |
x2 |
+ C. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||||||
2 |
|
2 |
2 |
|
|
|
4 |
|
|
|
|
|
|
||||||||
The result may be checked by differentiation.
Remark 1. The key to applying integration by parts is the correct choice of u and dv. Usually three conditions should be met:
First: v can be found by integrating and should not be too messy.
Second: du should not be messier than u.
Third: ∫vdu should be easier than the original ∫udv .
For instance ∫ x2e2x dx , with u = x2 and dv = e2xdx, meets these criteria. In this case v = e2x can be found and is not too messy; du = dx2 = 2xdx is easier than u as example 25 shows. ∫vdu is indeed simpler than ∫udv .
41. Find ∫ln xdx .
Solution.
∫ln xdx = |
u = ln x du = |
dx |
= x ln x − ∫ x |
dx |
= x ln x − x + C. |
||||||||||
x |
|||||||||||||||
|
|
|
|
|
|
|
x |
||||||||
|
dv = dx v = x |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||
42. Find ∫ln2 xdx. |
|
|
|
|
|
|
|
|
|
|
|||||
Solution. ∫ln2 xdx = |
|
u = ln |
2 |
x du |
= |
2ln xdx |
|
= x ln2 x − |
|||||||
|
|
||||||||||||||
|
|
x |
|
||||||||||||
|
|
|
|
dv = dx v = x |
|
|
|
|
|||||||
|
− 2∫ |
x ln xdx |
= x ln x2 − 2∫ln xdx. |
|
|||||||||||
|
|
|
|||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
By example 41 ∫ln xdx = x ln x − x + C. Thus: ∫ln2 xdx = x ln2 x − 2x ln x + x − C.
43. Find. ∫arctg 2xdx.
77
Solution. ∫arctg 2xdx = |
u = arctg 2xdx du = |
|
|
|
2dx |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
1+ 4x2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dv = dx v = x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
= x arctg 2x |
− ∫ |
|
2xdx |
|
= |
|
1+ 4x2 = t |
|
|
=x arctg 2x − |
1 |
∫ |
|
8xdx |
= |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
4 |
2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1+ 4x |
|
|
|
|
|
dt = 8xdx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ 4x |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
= x arctg 2x − |
1 |
∫ |
dt |
|
= x arctg 2x − |
1 |
ln |
|
t |
|
|
+ C = |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
t |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= x arctg 2x − |
1 |
ln (1+ 4x2 )+ C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
44. Find ∫ x2e2 xdx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Solution. ∫ x |
2 |
|
2 x |
|
|
|
|
|
|
|
u = x2 |
|
|
du = 2xdx |
|
|
1 |
|
2 |
|
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
e |
dx = |
dv = e2 xdx v = |
1 |
e2x |
|
= |
x |
e |
− |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
− ∫ 2 e |
|
2xdx = |
2 x |
e |
|
|
|
− ∫ xe |
|
|
|
dx = |
|
u = x du = dx |
2x |
|
= 2 x |
e |
|
− |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 x |
2 x |
2 x |
dv = e |
2xdx v = 1 e |
|
2 x |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
1 |
xe2x + ∫ |
|
1 |
e2x dx = |
1 |
x2e2x − |
1 |
xe2x + |
1 |
e2x |
+ C. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
4 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Integration by parts with u = x3 could be used to express |
|
∫ x3e2xdx |
in terms |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
of ∫ x2e2 xdx. Another integration by parts with u = x2, then expresses |
∫ x2exdx |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
in terms of |
∫ xexdx, as was done in Example 25. Each time integration by parts |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
lowers the exponent by 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
45. Find ∫(x2 − 2x + 5)e− x dx . |
|
|
|
|
|
|
|
|
|
|
|
|
dv = e− x dx , therefore |
|
v = −e− x |
||||||||||||||||||||||||||||||||||||||||||||||||
Solution. In this case |
|
u = x2 − 2x + 5 and |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
and du = (2x − 2)dx .Hence
∫(x2 − 2x + 5)e− x dx = −(x2 − 2x + 5)e− x + 2∫(x − 1)e− x dx .
Using another integration by parts to the last integral:
u = x − 1 , dv = e− x dx , du = dx , v = −e− x ,
∫(x − 1)e− x dx = − (x − 1)e− x + ∫e− x dx = −(x − 1)e− x − e− x + C1 = − xe− x + C1 . Thus
∫(x2 − 2x + 5)e− x dx = −(x2 − 2x + 5)e− x − 2xe− x + C = −(x2 + 5)e− x + C .
78

Remark 2. If P(x) is a polynomial of the form
∫ P(x)eαx dx = Q(x)eαx + C ,
where Q(x) is a polynomial which has the same degree of P(x) , then the
indeterminate coefficient method is used. The following example shows how to integrate in this case.
46. Find ∫(x3 + 18)e2x dx . |
|
|
|
|
|
|
|
||||
Solution. |
∫(x3 + 18)e2x dx = (Ax3 + Bx 2 + Cx + D)e2x + C1 , |
where |
|||||||||
A, B, C, D are unknown coefficients. |
|
||||||||||
Differentiating both parts of the expression with respect to х: |
|
||||||||||
(x3 + 18)e2x = (3Ax2 + 2Bx + C)e2x + 2(Ax3 + Bx2 + Cx + D)e2x , |
|
||||||||||
then |
|
|
|
|
|
|
|
|
|
|
|
x3 + 18 = (3Ax 2 + 2Bx + C) + 2(Ax3 + Bx2 + Cx + D) , |
|
||||||||||
x3 + 18 = 2Ax3 + (3A + 2B)x 2 + (2B + 2C)x + C + 2D . |
|
||||||||||
Since, the coefficients of the same degrees of х are equal and we have |
|
||||||||||
|
|
1 = 2A, 0 = 3A + 2B, 0 = 2B + 2C, 18 = C + 2D, |
|
||||||||
therefore A = |
1 |
, B = − |
3 |
, C = |
3 |
, |
D = |
69 |
. |
|
|
2 |
4 |
|
4 |
|
8 |
|
|
||||
Hence |
|
|
|
|
|
1 |
(4x3 − 6x2 + 6x + 69)e2x + C1 . |
|
|||
|
∫(x3 + 18)e2x dx = |
|
|||||||||
|
8 |
|
|||||||||
Remark 3. Reduction or recursion formulas. Many formulas in a table of integrals express the integral of a function that involves the n-th power of some expression in terms of the integral of a function that involves the (n – 1)-th or lower power of the same expression. These are reduction formulas. Usually they are obtainned by an integration by parts as examples 47 and 48 shows.
47. Find ∫cosln xdx .
Solution. Letting u = cosln x and dv = dx we have
du = − sin ln x |
dx |
, v = x , |
∫cosln xdx = x cosln x + ∫sin ln xdx . |
x |
Using other integration by parts to the last integral:
u = sin ln x , dv = dx , du = cosln x dxx , v = x ,
∫sin ln xdx = x sin ln x − ∫cosln xdx .
Since
∫cosln xdx = x cosln x + x sin ln x − ∫cosln xdx , 79
therefore
|
|
|
|
|
|
|
|
|
|
|
∫cos ln xdx = |
1 |
|
(x cos ln x + x sin ln x) + C . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
48. Find ∫ |
|
|
|
dx |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
(x2 + a)n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Solution. ∫ |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
∫ |
|
|
|
|
|
a |
|
|
|
|
|
|
|
1 |
|
∫ |
a + x2 − x |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dx = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = |
|
|
|
|||||||||||||||||||||||||||||||||||
(x2 + a)n |
|
a |
|
|
|
(x2 + a)n |
|
|
a |
|
(x2 + a)n |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
a + x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2dx |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
dx |
1 |
|
|
|
|
|
x xdx |
|
|
|||||||||||||||||||||||||||||||||||||||||||
= |
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
dx − ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
∫ |
|
|
|
|
|
= |
||||||||||||||||||||||||||
2 |
|
(x2 + a)n |
(x2 + a)n |
|
|
|
2 |
|
(x2 + a)n−1 |
|
a |
|
(x2 + a)n |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
u = x du = dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
∫ |
|
|
|
|
|
|
dx |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xdx |
|
|
|
|
|
|
|
v = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
= |
|
|
dv = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
− |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2(1− n)(x2 + a)n−1 |
|
a |
(x2 + a)n−1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(x2 + a)n |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
dx |
|
|
|
|
|
1 |
|
∫ |
|
|
|
|
|
dx |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
− |
||||||||||||||||||||||||||||||||||||||||||||||||||
a |
2(1− n)(x2 + a)n−1 |
2(1− n) |
(x2 + a)n−1 |
a |
|
(x2 + a)n−1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
1 |
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
dx |
|
|
= |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2a(1− n)(x2 + a)n−1 |
2a(1− n) |
|
(x2 + a)n−1 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
2(1− n)+ 1 |
∫ |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a(1− n) |
|
(x2 + a)n−1 |
|
2a(1− n)(x2 + a)n−1 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Hence |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n − 3 |
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
∫ |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
∫ |
|
|
. |
|
(2.3) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
(x2 + a)n |
2a(n − 1)(x2 + a)n−1 |
|
|
2a(n − 1) |
(x2 + a)n−1 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
This is a reduction formula. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
For example, this formula is spelled in the following case. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
J1 = |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
= |
|
|
1 |
|
arctg |
x |
|
+ C is the table integral; |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
∫ x2 + a2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
J 2 = |
∫ |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
= |
1 |
|
|
|
|
|
|
|
|
|
x |
|
+ |
1 |
|
1 |
J1 = |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
(x2 + a 2 )2 |
2a 2 |
|
x 2 + a 2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
a 2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
1 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
+ |
|
|
|
1 |
|
|
|
|
arctg |
x |
+ C etc. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a3 |
|
a |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 + a 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
49. Find J n, −m = |
|
|
|
sin n x |
|
dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
∫ cosm x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
80 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
