Higher_Mathematics_Part_2

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный авиационный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Find the volume of the solid bounded by the paraboloid

and the plane z = 1 .

Find the volume of the solid bounded by the hyperboloid of one sheet

.pdf

Скачиваний:

408

Добавлен:

19.02.2016

Размер:

7.48 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1718 / 2518 19 20 21 22 23 24 25 > Следующая >>>

At the point N xN = 0 , thereby cos t = 0 and t N

intersection of the line and ellipse, thereby 2 3 = 4 sin t The area of the rectangle OMCD is equal to:

SOMCD = OM MC = 2 3 6 cos	π	=
Evaluating the area of the region ONCD :	3
Evaluating the area of the region ONCD :

= π2 . The point C , sin t = 23 , tC =

6 3 .

		SONCD = ∫3		4 sin td(6 cos t) = − 24∫3 sin 2 tdt =
			π					π
	π	2						2
						π
						π
	2
	2				sin 2t	2			π		π
	∫				sin 2t				π		π
12		(1− cos 2t)dt = 12 t −					=	12		−		+
12		(1− cos 2t)dt = 12 t −					=	12		−		+
					2				2		3
	π				2	π			2		3
	π					π
						3
	3					3
	3

24∫2 sin 2 tdt =

	3
			= 2π+3 3 .
	4		= 2π+3 3 .
	4

is the

π3 .

Hence, S = 2(2π + 3 3 − 6 3) = 4π − 6 3 .

5. Find the area of the region bounded by the Bernoulli’s lemniscate (x2 + y 2 )2 = x2 − y 2 (fig. 2.18).

	y N		ϕ =	π
	y N		ϕ =	4
B		C	у
B	M	C	S1
	M		S1
A	O	D x		х
	Fig. 2.17		Fig. 2.18

Solution. Transform the given equation into a corresponding polar equation. In this case the substitutions x = ρcos ϕ , y = ρsin ϕ are appropriated

ρ 4 = ρ 2 (cos2 ϕ − sin 2 ϕ) , thereby ρ = cos 2ϕ .

Notice that there is symmetry with respect to the x axis and y axis. Consequently,

				π
		1	4				π
S = 4S1	= 4	1		∫0	cos 2ϕ d ϕ = sin 2ϕ		4	= 1 .
S = 4S1	= 4	2			cos 2ϕ d ϕ = sin 2ϕ		4	= 1 .
		2				0
6. Find the area of the region bounded by the curves ρ = 6 sin 3ϕ and ρ = 3
( ρ ≥ 3 ).
					171

		π
		3	π
	ρ=3		π
	ρ=3	B	6
		B	6
		C	π
		C	18
			18
О		A
		A
		ρ = 6

Fig. 2.19

Solution. The curve ρ = 6 sin 3ϕ is called a three-leaved rose. As ϕ

increases from 0 up to

, 3ϕ increases from 0 up to π. Thus ρ, which is sin 3ϕ,

goes from 0 up to 6, then back to 0, for ϕ in

. This gives one loop of the

2π

three loops making up the graph of ρ = 6 sin 3ϕ . For 0 in

, ρ = 6 sin 3ϕ

is negative (or 0). This yields the lower loop in fig. 2.19. For ϕ in	2π		, ρ is
		, π

	3

again positive, and we obtain the upper left loop. Further choices of	ϕ lead only

to repetition of the loops already shown.

The second function ρ = 3 is the circle. For ρ ≥ 3 the given area S is shaded

in fig. 2.21 and is equal to S = 6S ABCA .
Finding the polar coordinates of			А		and В:	6 sin 3ϕ = 3 , sin 3ϕ =	1	,
							2
	π			π
ϕ A =		. There is В on the ray with ϕ B	=		.
				6
18

As is shown the area of S ABCA = SOABO − SOACO , where ОАСО is a sector that is subtended by a central angle π6 . Evaluating the area of it:

SOACO = 12 R 2 α = 12 9 π6 −18π = π2 .

172

Thereafter

SOABO =

∫6

36 sin 2 3ϕdϕ = 9 ∫6

(1− cos 6ϕ)dϕ = 9(ϕ −

sin 6ϕ

)

= π +

3 3 .

Hence

S = 6

−

= 3π +

Arc length

7. Find the arc length of the curve y =x2 for x in [0,1] .

Solution. By the given formula l = ∫b

1+ (y′)2 dx.

Since y = x2,

y′ = 2x. Thus l = ∫1

1 + 4x2 dx =

2x = tdt dx =

1 arctg 2

2cos2 t

∫0

sec3 tdt =

cos3 t

x = 0 t = 0; x = 1 t = arctg 2

arctg 2

tg t 1+ tg

arctg 2

sect tg t

∫

sectdt

1 arctg 2 sect (sect + tg t )

1 arctg 2 sec2 t + sect tg t

∫

dt =

sect + tg t

arctg 2

sect + tg t

1+ tg2 t

+ tg t

2 5

ln( 5 +2) .

8. Find the length of one arch of the cycloid

x = a(t − sin t) , y = a(1− cos t) Solution. Here the parameter is t and we compute xt/

xt/ = a(1− cos t);yt/ = a sin t.

and yt/ :

173

(xt/ )2 +(yt/ )2 dϕ .

To complete, one arch varies from 0 to 2π (see fig. 2.20). By given formula

the length of one arch is: l = ∫

•

О•

2πa

Fig. 2.20

Hence

2π

t dt =

l = ∫

a 2 (1− cos t)2 + a 2 sin 2 tdt = a ∫

2 − 2 cos tdt = a ∫

4 sin 2

2π

= 2a ∫

2a ∫sin

4a cos

= 8a .

sin

dt =

= −

9. Find the arc length of the curve ρ = sin ϕ (fig. 2.21).

Solution. Since ρ ≥ 0, then 0 ≤ ϕ ≤ π. Hence

l = ∫

sin2 ϕ + cos2 ϕdϕ = ∫dϕ = π .

0,5

Remark. It is no surprise that the graph appears to be a

О•

circle.

The

equation

rectangular

coordinates

that

x corresponds

the

polar

equation

ρ = sin ϕ

Fig. 2.21

x 2 + ( y − 1/ 2)2 = 1/ 4 .

Volume of a solid

10. Find the volume

the

solid

bounded by

the

paraboloid

z = x

y 2

and

cone

y 2

= z

(fig. 2.22).

Solution. There is a region between the paraboloid and

cone. The volume V of it is equal to

V = Vп − Vк ,

where Vn is the volume of the paraboloid between the point

z = 0 and the plane z = 1 (they are the roots of the equation

Fig. 2.22

z = z 2 ) and Vk is the volume of the cone between them.

174

x 2

y 2

The perpendicular

section

axis

are

the

ellipses

( z )2 + (2

z )2

= 1

(with the paraboloid)

and

x 2

y 2

= 1

(with the cone). As is

generally

(2z)2

known the area of ellipse

x 2

y 2

= 1 is πab.

a 2

Hence

V = Vп − Vк = π∫

z 2

zdz − π∫ z 2zdz = π∫ 2zdz − π∫ 2z 2 dz =

= πz

−

πz

11. The region between

x 2 + y 2

= 1,

y =

2x 2

and x = 0 ( x ≥ 0 )

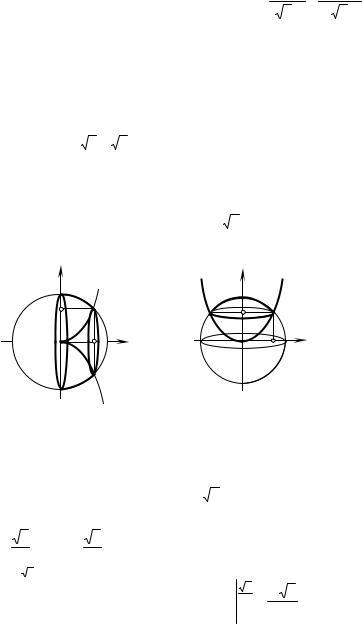
revolved around the a) x axis (fig. 2.23); b) y axis (fig. 2.24). Find the volume of the solids of revolution produced.

			y		1																			у		1
										x																			1	х
									1	x																			1	х


			Fig. 2.23																					Fig. 2.24


Solution. Evaluating the system
										2			3			x 2				+ y 2			= 1,
										2	= x		3	,										2
									y		= x			,						=		2x		2	,
										2 = 16x						y				=		2x			,
									y	2 = 16x
																				> 0,
	2						2									x				> 0,
we get x =	2		and	y =			2	. Thereafter
	2						2
		2
	2																x		3		2					2		11 2
а) V = π ∫[(1− x					2	) − 2x		4	]dx =								x				2		5 2					11 2
а) V = π ∫[(1− x						) − 2x			]dx =			π x			−			3		−	5	x					=	30		π ;
	0																	3			5			0				30
													175

	2									y3	1
	2	y		1			y2		2						16 − 7	2
	∫	y		∫		− y2 )dy = π	y2						2		16 − 7	2
	∫			∫									2
b) V = π			dy + π		(1				2 + π y −					=			π .
	0	2		2			2 2	0		3					24
	0	2		2			2 2	0		3		2			24

				2

В(0; a) A(a; 0)

12. The asteroid x = a cos3 t , y = a sin 3 t

(fig. 2.25) is revolved around the x axis. Find the volume of the solids of revolution produced.

Solution. Notice that there is symmetry with respect to the x axis. We can find only the volume of

ООАВ, which is revolved around the x axis and multiple

xthe result by 2:

																				a
	Fig. 2.25																V = 2π∫ y 2 (x)dx .
	Fig. 2.25																			0
							This prompts the following maneouver:
	x = a cos3 t ,						dx = −3a cos2 t sin tdt ,													y = a sin 3 t .
If	x = 0 , then tB =			π	and if				x = a , then t A = 0 .
If	x = 0 , then tB =				and if				x = a , then t A = 0 .
	2
Hence
																					π
	0
	V = 2π∫ (a sin 3 t)2 (−3a) cos2 t sin tdt = 6πa3 ∫2 sin 7 t cos2 tdt =
		π																		0
		2 π															π							π

	= 6πa3 ∫2 sin 7 t(1− sin 2 t)dt = 6πa3 (∫2 sin 7 tdt − ∫2 sin 9 tdt) =
	0																0			0
			= 6πa3 (			6		4		2	−		8	6		4	2	) =		32			πa3 .
			= 6πa3 (			7					−			7			3	) =	105				πa3 .
						7	5		3		9			7	5		3		105
												π										π

We used the reduction formula: ∫2 sin n xdx =			n − 1	∫2 sin n−2 xdx .
We used the reduction formula: ∫2 sin n xdx =			n	∫2 sin n−2 xdx .
		0	0
		Exercises for class and homework
	Т.8	Exercises for class and homework

Find the area of the region bounded by the given curves (or lines).

1.	xy = 4 , y = 1, y = x + 3 .
2.	y = x 2 − 3x + 3 , y = − x 2 + x + 9 .
3.	y 2 − 2 y − 2x − 3 = 0 , y − x + 1 = 0 .
	176

4. y = tg x , y = sin x − 2 , x = − π4 , x = π4 .

5.y = 16 , y = 17 − x 2 .

6.	xy = 20 ,		x 2 + y 2 = 41 (Quadrant І).
7.	y =	1		, 2y = x 2 .
		+ x 2
	1

8.y = 0 , y = arcsin x , y = arccos x .

9.ρ = 2 sin 2ϕ .

10.ρ = 4 cos 2ϕ , ρ = 2 ( ρ ≥ 2 ).

11.ρ = 2 + cos ϕ .

12.ρ = sin 2 ϕ2 (righter of ray ϕ = π2 ).

13. ρ =	4	, ϕ =	π	, ϕ =	π	.
	cos(ϕ − π / 6)		6		3

14.(x 2 + y 2 )3 = 4xy(x 2 − y 2 ) .

15.x 4 + y 4 = x 2 + y 2 .

16.	x = a cos3 t ,		y = b sin 3 t .
17.	x 2	+ y 2 = 1,	x = 1 ( x ≥ 1).
	4

18.x = 2(t − sin t) , y = 2(1− cos t) , y = 1( y ≥ 1 ). Find the arc length.

19.y = ln x from x = 3 to x = 8 .

20. y = ln(1− x 2 )				from x = 0 to			x =		1		.
20. y = ln(1− x 2 )				from x = 0 to			x =				.
								2
21.	y = ln sin x from x =				π	to	x =	π		.
				3				2
22.	y =	x 2	from	x = 0 to		x = 1 .
22.	y =	2	from	x = 0 to		x = 1 .
		2

23.x = 9(t − sin t) , y = 9(1− cos t) (only one arch of the cycloid) .

24.x = 8 sin t + 6 cos t , y = 6 sin t − 8 cos t , 0 ≤ t ≤ π2 .

177

25.	x =	t 3	− t ,		y = t 2 + 2 ,		0 ≤ t ≤ 3 .

	3
26.	y = x − x 2				+ arcsin		x .
27.	x = a cos5 t , y = a sin 5 t .
28.	ρ = sin		3 ϕ	,	0 ≤ ϕ ≤	π	.
			3			2

29.ρ = 1+ cos ϕ .

30.ρ = ϕ 2 , 0 ≤ ϕ ≤ π .

31.ρ = ϕ1 , 34 ≤ ϕ ≤ 43 .

x 2

the

+	y 2	− z 2 = 1 and the planes z = −1 and z = 2 .

9

The region bounded by the given curves is revolved around the x axis. Find volume of the solid of revolution produced.

34. y =	64	, 8y = x 2 .	35. y 2 = x , y = x 2 .
	+ x 2
16

Answers

1. 4ln 4 + 3/ 2 . 2. 22	2	. 3. 18. 4. π. 5. 18.	6.	41	arcsin	9	+ 20ln 0,8 .	7.	π	−	1	.
	3			2		41			2		3

						π																	8	3
8.	2 − 1 . 9. π . 10.							+			. 11. 9π / 2 . 12. (3π − 8) / 32 .									13.			8	3	.	14. 1.						15. π			2 .
8.	2 − 1 . 9. π . 10.					4	3	+		3	. 11. 9π / 2 . 12. (3π − 8) / 32 .									13.			3		.	14. 1.						15. π			2 .
							3																3
16.	3	πab . 17.		2π		−	3 .			18.		16		π + 5 3 .	19. 1 +		1		ln	3	.		20.		ln 3 −			1	.		21.		1	ln 3 .
	8				3		2					3				2				2							2						2
	1																										1
22.			2 +ln(1	+	2 )		.	23. 72.						24. 5π . 25. 12.		26. 2. 27.							5a	1+						ln	(	2 +	3		)
22.	2		2 +ln(1	+	2 )		.	23. 72.						24. 5π . 25. 12.		26. 2. 27.							5a	1+						ln		2 +	3		.
	2																									2	3
	1											1						5				3				2	3
28.	1		(2π − 3 3) .		29.		8.			30.		1	((π2 + 4)3/ 2		− 8) . 31.			5		+ ln		3	. 32.			2π .					33.			36π .
28.	8		(2π − 3 3) .		29.		8.			30.		3	((π2 + 4)3/ 2		− 8) . 31.	12				+ ln		2	. 32.			2π .					33.			36π .
	8								3			3				12						2
34.	16π(3π + 10) /5. 35.								3	π .
34.	16π(3π + 10) /5. 35.							10		π .
								10

178

Т.8 Individual test problems

8.1. Find the area of the region bounded by the given curves (or lines).

8.1.1. y = x2 − 2x − 1 , 2y = 3x − 2 .					8.1.2. 4y = x2 , 2y = 6 − x2 .
8.1.3. x = y 2 − 2 y , x = − y 2 + 2y + 6 .					8.1.4. y = x 4 − x , y = 0 .
8.1.5. y = x2 −6x +6,			y =−x2 +2x .		8.1.6. x = y 2 − 2 , y = − x .
8.1.7. y = x2 + 4x + 2 ,			y = 2 + x .		8.1.8. x = y 2 − 2y − 2 , y = − x .
8.1.9. x = y 2 + 2y − 2 , y = −2 − x .					8.1.10. y = x arctg x , 0 ≤ x ≤ 1 .
8.1.11. y =	1	, y = 0 , x = 0 , x = 4 .			8.1.12. y = x2 +5x, y = 7 −x .
1	+	x
8.1.13. x = y 2 − 2y − 1,			y = 1 − x .		8.1.14. y = 3x −4, y =−x2 .
8.1.15. x = y 2 + 2y − 1,			y = −1 − x .		8.1.16. y2 = 4 − x, x = y2 − 2 y .
8.1.17. y = x tg2 x , 0 ≤ x ≤ π / 4 .					8.1.18. y = x2 + 6x, y = − x2 .
8.1.19. y = cos3 x sin 2x , 0 ≤ x ≤ π / 4 .					8.1.20. y = xcos2 x , 0 ≤ x ≤ π / 2 .
8.1.21. y = x	4 − x2 , y = 0 , 0 ≤ x ≤ 2 .				8.1.22. y = xsin2 x, 0 ≤ x ≤ π / 4 .
8.1.23. y = sin 4 x sin 2x , 0 ≤ x ≤ π / 3 .					8.1.24. y = x2− 4x + 2, y = 2 − x.
8.1.25. y =	x	, y = 0 ,		0 ≤ x ≤ 1 .	8.1.26. x =y2+2 y +3, x=8−2 y.
1	+	x
8.1.27. y = 2x 2 − 12x + 16 ,				y = x 2 − 5x + 4 .
8.1.28. y = x2 +8x +7,			y =−x2 −2x −5 .
8.1.29. y = x		9−x2 ,	y = 0 , 0 ≤ x ≤ 3 .
8.1.30. x = 2y 2 − 8y + 6 ,				x = y 2 − 3y .

8.2. Find the area of the region bounded by the indicated curve.

8.2.1.ρ =1+cos ϕ , ρ =1 ( ρ ≥1 ).

8.2.2.ρ = 2 +cos ϕ .

8.2.3.ρ =1+cosϕ , ρ =3 / 2 ( ρ ≤3/ 2 ).

8.2.4.ρ = 2−sin ϕ .

8.2.5.ρ =1+sin ϕ , ρ =1/ 2 ( ρ ≥1/ 2 ).

8.2.6.ρ =3−cos ϕ .

8.2.7.ρ =1−sin ϕ , ρ =1 ( ρ ≤1 ).

8.2.8.ρ = 2 +cos 2ϕ .

8.2.9.ρ =1−cos ϕ , ρ =1 ( ρ ≥1 ).

179

8.2.10.ρ =3+sin 2ϕ .

8.2.11.ρ =1−sin ϕ , ρ =3 / 2 ( ρ ≥3/ 2 ).

8.2.12.ρ =1+2cos ϕ .

8.2.13.ρ = 2 cos 2ϕ , ρ = 1 (ρ ≥ 1).

8.2.14.ρ =1+2sin ϕ .

8.2.15.ρ = 4 sin 2ϕ, ρ = 2 (ρ ≥ 2).

8.2.16.ρ = cosϕ + sinϕ.

8.2.17. ρ = 6 cos 3ϕ, ρ = 3	3 ( ρ ≥3 3 ).
8.2.18. ρ =cosϕ – inϕ.
8.2.19. ρ = 2 sin 3ϕ, ρ =	3 ( ρ ≥ 3 ).

8.2.20.ρ = cos2 ϕ .

8.2.21.ρ = cos 2ϕ + sin 2ϕ.

8.2.22.ρ =sin2 ϕ .

8.2.23.ρ = 3 cos ϕ , ρ =sin ϕ .

8.2.24.ρ = 3 + cos 2ϕ.

8.2.25.ρ = tg ϕ , ϕ = π / 3 .

8.2.26.ρ = cos2 2ϕ .

8.2.27.ρ = 1+ tg ϕ , ϕ = π / 4 .

8.2.28.ρ = cos ϕ2 .

8.2.29.ρ = 4sin2ϕ , ρ = 2 3 ( ρ ≥ 2 3 ).

8.2.30.ρ = 2 − cos 2ϕ .

8.3.Find the area of the region bounded by the indicated curve.

8.3.1.x = 4 2 cos3 t, y = 2 2 sin3 t, x = 2 ( x ≥ 2 ).

8.3.2.x = 16 cos3 t, y = 2 sin3 t, x = 2 ( x ≥ 2 ).

8.3.3. x = 2 cos t, y = 6 sin t, y = 3 ( y ≥ 3 ).


8.3.4. x = 2(t − sin t), y = 2(1− cos t),				y = 3 ( y ≥ 3 , 0 ≤ x ≤ 4π ) .
8.3.5. x = 16 cos3 t, y = sin3 t, x = 2 ,				x = 6	3 ( 2 ≤ x ≤ 6 3 ).
8.3.6. x = 6 cos t, y = 2 sin t, y = 1 ,			y = 3 (1 ≤ y ≤ 3 ).
8.3.7. x = 3(t − sin t), y = 3(1− cos t),				y = 3	( y ≥ 3 , 0 ≤ x ≤ 6π ) .
8.3.8. x = 8	2 cos3 t, y =	2 sin3 t,	x = 4 ( x ≤ 4 ).
8.3.9. x = 2	2 cos t, y = 3	2 sin t,	y = 3 ( y ≥ 3 ).
8.3.10. x = 6(t − sin t), y = 6(1 − cost),			y = 3 ,		y = 9 ( 3 ≤ y ≤ 9 , 0 ≤ x ≤ 2π ).
8.3.11. x = 32 cos3 t, y = sin3 t, x = 4 ( x ≥					4 ).

180

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1718 / 2518 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.11.2018765.44 Кб6Hagakure_-_Sokrytoe_v_listve.doc
#
19.02.20166.95 Mб201Higher Mathematics. Part 3.pdf
#
19.02.20169 Mб95Higher_Mathematics_Part_1.pdf
#
19.02.20166.63 Mб1052Higher_Mathematics_Part_1.pdf
#
19.02.20169.73 Mб45Higher_Mathematics_Part_2.pdf
#
19.02.20167.48 Mб408Higher_Mathematics_Part_2.pdf
#
19.02.20167.31 Mб123Higher_Mathematics_Part_2.pdf
#
19.02.20169.11 Mб304Higher_Mathematics_Part_3.pdf
#
19.02.2016694.82 Кб11HiraganaKatakanaWorkSheet (1).pdf
#
11.09.2019192.23 Кб1hjuj;f.docx
#
27.11.2019386.05 Кб9How Airplanes Work.doc