
Higher_Mathematics_Part_2
.pdf
1
Conclusion. The second type of improper integral ∫ dx is convergent
0 xλ
if λ < 1 and is divergent if λ ≥ 1
Т.7 |
Exercises for class and homework |
Determine whether the improper integrals are convergent or divergent. Evaluate the convergent ones.
|
∞ |
|
dx |
|
|
|
|
|
|
∞ |
|
|
|
dx . |
|
|
|
|
|
|
|
|||||||
1. |
∫ |
|
. |
|
|
|
|
2. |
∫ |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
1 |
|
x |
|
|
|
|
|
|
|
|
1 |
5 |
x 2 |
|
|
|
|
|
|
|
|
|
|||||
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
∞ |
xdx |
|
|
|
|
|
|
||||||||
3. |
∫ e−3x dx . |
|
4. |
∫ |
. |
|
|
|
||||||||||||||||||||
|
2 |
|
|
|||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
−∞ |
1+ x |
|
|
|
|
|
|
|
|||||||
|
∞ |
|
|
|
|
dx |
|
|
∞ |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
||||||
5. |
∫ |
|
|
|
|
|
. |
6. |
∫ |
|
|
|
|
|
|
|
|
|
. |
|
|
|||||||
|
x |
2 |
− |
2x + 10 |
|
(1+ x)x |
2 |
|
|
|||||||||||||||||||
|
−∞ |
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||||||||
|
∞ |
|
|
|
|
|
|
2 |
|
|
|
|
∞ arctg x |
|
|
|
|
|
|
|
||||||||
7. |
∫ xe− x |
|
dx . |
|
8. |
∫ |
|
|
|
|
|
|
|
|
|
dx . |
|
|
||||||||||
|
|
|
|
|
x |
2 |
|
|
|
|
|
|||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
dx . |
|
|
|
2 |
|
|
|
|
|
dx |
|
|
||||||||||
9. |
∫ |
|
|
|
|
|
10. |
∫ |
|
|
|
|
. |
|||||||||||||||
|
|
|
|
|
x |
2 |
− 4x + |
3 |
||||||||||||||||||||
|
0 |
|
|
|
1− x 2 |
|
|
|
0 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
xdx |
|
|
|
|
e |
|
|
dx |
|
|
|
|
|
|
|
||||||||
11. ∫ |
|
|
|
|
|
. |
|
12. ∫ |
|
|
|
|
|
|
|
|
. |
|
|
|||||||||
|
|
x − |
|
x ln |
2 |
|
|
|
|
|
||||||||||||||||||
|
|
1 |
|
|
|
1 |
|
|
|
0 |
|
|
x |
|
|
|||||||||||||
Determine whether the improper integrals are convergent or divergent
|
∞ |
xdx |
|
|
|
|
∞ |
x3 + 1 |
|
|
|
|||
13. |
∫ |
. |
|
|
14. |
∫ |
dx . |
|||||||
3 |
|
|
4 |
|||||||||||
|
0 |
1+ x |
|
|
|
|
|
1 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
∞ ln(1+ x |
2 )dx |
|
|
∞ |
dx |
|
|
|
|
||||
15. |
∫ |
|
|
|
. |
16. |
∫ |
|
|
. |
||||
|
x |
|
x ln ln x |
|||||||||||
|
1 |
|
|
|
|
|
|
e2 |
|
|
|
|
|
|
|
1 |
xdx . |
|
|
1 |
|
dx |
|
|
|||||
17. |
∫ |
|
18. |
∫ |
|
. |
||||||||
|
|
|
||||||||||||
|
0 |
1− x 4 |
|
|
|
0 |
|
e x − 1 |
|
|
||||
|
1 |
dx |
|
|
|
|
|
1 |
|
dx |
|
|
||
19. |
∫ |
|
. |
|
|
20. |
∫ |
|
|
. |
||||
sin x |
|
|
x + |
3 |
||||||||||
|
0 |
|
|
|
|
|
0 |
|
|
|
x |
|||
|
|
|
|
|
|
|
161 |
|
|
|
|
|
|
|

π |
|
sin xdx . |
|
|
0 |
|
|
|
dx . |
|
|
||||||||
7.2.17. ∫ |
|
|
7.2.18. |
∫ |
|
|
|
|
|
||||||||||
π / 2 |
7 cos2 |
x |
|
−3 / 4 |
|
4x + 3 |
|
|
|||||||||||
2 |
|
|
|
|
xdx |
|
1/ 3 |
|
|
|
dx |
|
|
|
|
||||
7.2.19. ∫ |
|
|
|
|
. |
7.2.20. ∫ |
|
|
|
|
|
|
. |
||||||
|
(x2 − 1)3 ln 2 |
|
2 |
− |
9x + |
2 |
|||||||||||||
1 |
|
|
0 |
9x |
|
|
|||||||||||||
3 |
3 9xdx . |
|
π / 2 |
3sin 3 xdx . |
|||||||||||||||
7.2.21. ∫ |
|
7.2.22. |
∫ |
|
|||||||||||||||
0 3 9 − x2 |
|
|
|
0 |
|
|
|
cos x |
|
|
|||||||||
1 |
|
x4 dx5 . |
|
2 |
|
|
x2 dx |
|
6 . |
|
|
||||||||
7.2.23. ∫ |
3 |
|
7.2.24. ∫ |
|
|
|
|
|
|||||||||||
0 |
|
1 − x |
|
|
0 |
|
64 − x |
|
|
|
|
|
|||||||
1 |
|
|
|
dx |
|
|
5 |
|
|
x2 dx |
|
|
|
|
|||||
7.2.25. ∫ |
|
|
|
. |
|
7.2.26. ∫ |
|
|
|
|
. |
|
|||||||
9 |
1 |
− 2x |
|
|
31(x3 − 1`) |
|
|||||||||||||
1/ 2 |
|
|
|
1 |
|
|
|
||||||||||||
1/ 4 |
|
|
dx |
|
|
4 |
|
|
10xdx |
|
|
||||||||
7.2.27. |
∫ |
|
|
|
. |
|
7.2.28. ∫ |
|
|
. |
|||||||||
3 |
|
|
|
4 (16 − x2 `)3 |
|||||||||||||||
|
0 |
|
|
1 − 4x |
|
0 |
|
|
|||||||||||
3 / 2 |
|
|
dx |
|
1/ 2 |
|
|
dx |
|
|
|
|
|
|
|||||
7.2.29. |
∫ |
|
|
|
. |
7.2.30. ∫ |
|
|
|
|
|
. |
|
|
|||||
|
|
3x − x2 − 2 |
(2x − 1) |
2 |
|
|
|||||||||||||
|
1 |
|
|
|
0 |
|
|
|
|
||||||||||
Topic 8. Application of the definite integral
Finding the area of a region. How to find the arc length. Computing volume by parallel cross sections. Computing the volume of a solid of revolution. The centroid of a plane region. Work.
Literature: [1, section 9], [2, section 2, ch. 2.2], [4, section 7, §24], [6, section 10], [7, section 12], [9, § 41].
Т.8 |
Main concepts |
8.1. Computing areas
8.1.1. Area in rectangular coordinates
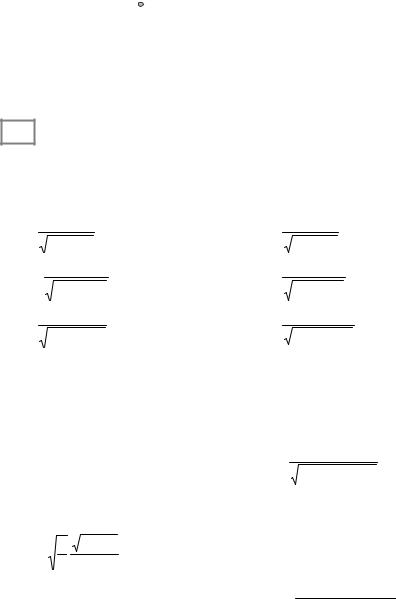
Consider the area of the region bounded by y = f (x) ( f (x) ≥ 0 ) and the
x- axis from x = a to x = b, as shown in fig. 2.5. The area S of the entire region is found by
b
S = ∫ f (x)dx.
a
164
However, if a function changes the sign finitely in [a; b] (fig. 2.6) the area is found according to the following formula
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S = ∫ |
|
f (x) |
|
dx . |
|
|
|
||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
y= f(x) |
|
|
|
|
|
|
|
|
y = f(x) |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
S |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
c |
d |
|
О |
|
|
|
|
|
|
|
О |
|
|
b |
|||
a |
|
b x |
|
|
||||||||||
|
|
Fig. 2.5 |
|
|
|
|
|
|
Fig. 2.6 |
|
||||
Let f1 and f2 be two continuous functions such that |
f1 (x) ≤ f 2 (x) for all x in |
|||||||||||||
the interval [a, b]. Let S be the region between the curve y = f1 (x) and the curve y = f 2 (x) for x in [a, b], as shown in fig. 2.7. The area of S is then given by
b
S = ∫[ f2 (x) − f1(x)]dx
a
It should be obvious to you that knowing the points of intersection is important in determining the limits of integration. For instance, the sketch of the region appears in fig. 2.8. To find where the curves intersect, we solve the
system of equations y = f1 (x) |
and |
y = f 2 (x) . In this case, if x1 < x2, then a = x1 |
|||||||
and b = x2. |
|
|
|
|
|
|
|
|
|
y |
|
y=f2(x) |
|
|
|
y |
y=f2(x) |
||
|
|
|
|
||||||
|
|
S |
|
|
|
|
|
||
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
|
|
y=f1(x) |
|
|
|
|
y=f1(x) |
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
О |
a |
b |
x |
О a |
|
b x |
|||
|
|
Fig. 2.7 |
|
|
|
|
Fig. 2.8 |
||
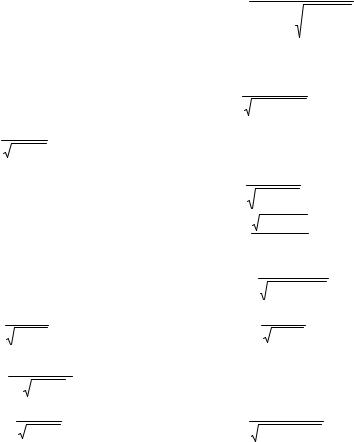
Sometimes area can more easily be determined by summing areas of horizontal elements rather than vertical elements. Let S be the region between
the curve x = g1 ( y) and the curve x = g 2 ( y) for y in [c, d], as shown in fig. 2.9 and 2.10. The area of S is then given by
d
S = ∫[g2 ( y) − g1 ( y)]dy.
c
165

The length l in polar coordinates of the curve ρ = ρ(ϕ) for ϕ in [ϕ1, ϕ2] is equal to
ϕ |
ρ2 (ϕ) + (ρ′ (ϕ))2 dϕ |
l = ∫2 |
|
ϕ1 |
|
8.3. Volume of a solid
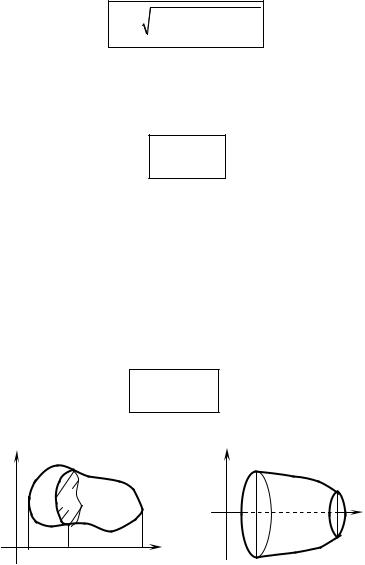
8.3.1. Computing volume by parallel cross sections
The volume V of a spatial region, a “solid”, can be expressed as a definite integral of cross-section area S(x),
b
V = ∫ S (x)dx
a
as shown in fig. 2.12. So, to find the volume of some solid, follow these steps:
1.Choose a line to serve as an x axis.
2.For each plane perpendicular to that axis find the area of the cross section of the solid made by plane. Call this area S(x).
3.Determine the limits of integration, a and b, for the region.
4.Evaluate the definite integral ∫b S(x)dx .
a
8.3.2. Computing the volume of a solid of revolution
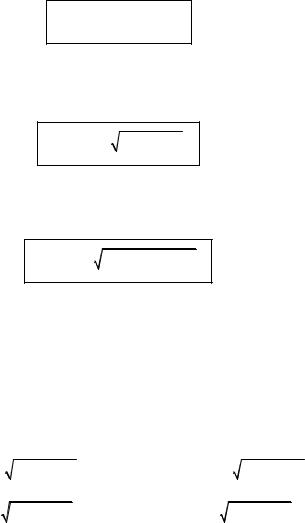
Let y = f(x) be a continuous function such that f(x) ≥ 0 for x in the interval [a, b]. The curve y = f(x) is revolved around the x axis to form a solid of revolution (see fig. 2.13). The volume V of a solid is then given by
|
|
b |
|
|
|
|
V = π∫ f 2 (x)dx. |
|
|
|
|
a |
|
|
y |
|
y |
|
y=f(x) |
|
S(x) |
|
|
|
|
|
О |
a |
b x |
О a |
x |
b x |
|
|
|
Fig. 2.12 |
|
|
Fig. 2.13 |
|
|
167 |
|
|
Let y = f1(x) |
and y = f2(x) be two continuous functions such that |
0 ≤ f1 (x) ≤ f 2 (x) |
for x in the interval [a, b]. Let S be the region bounded by the |
curves y = f1(x) and y = f2(x) and above [a, b]. The region S is revolved around the x axis to form a solid of revolution. The volume V of a solid is then given by
b
V = π∫[ f22 (x) − f12 (x)] dx.
a
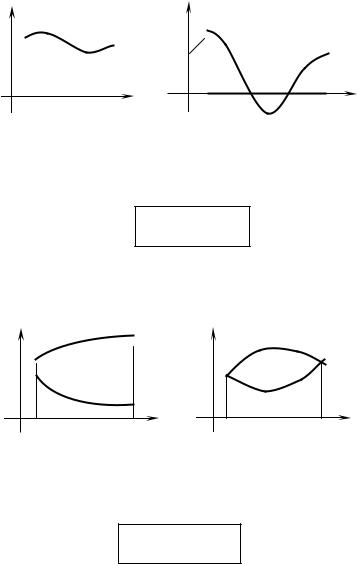
8.4. Area of a surface of revolution
Let y = f(x) be a continuous function such that f(x) ≥ 0 for x in the interval [a, b] and f(x) has a continuous derivative. A formula for surface area P if y = f(x)
( a ≤ x ≤ b ) is revolved around x axis is given by
b
P = 2π∫ f (x) 1+ ( f ′(x))2 dx.
a
If a curve is given by the parametric equations x = x(t) and y = y(t) , where
x(t) and y(t) have continuous derivatives and y(t) ≥ 0. Let C be that portion of the curve corresponding to t in [α, β]. Then the area of the surface of revolution formed by revolving C about the x axis is
β
P = 2π∫ y(t) (x′(t))2 + ( y′(t))2 dt.
α
|
8.5. Work |
|
|
|
|
|
|
|
|
||||||
|
Work A of variable force F(x), if a point M is traveled from х = а to х |
||||||||||||||
= b, |
а < b, can be calculated by the integral: |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = ∫ F(x)dx. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
8.6. The centroid |
|
|
|
|
|
|
|
|
||||||
|
The centroid of a curve l, such that has an equation y = f (x) , x [a, b] |
|
is |
||||||||||||
defined as the point (xc, yc), where |
|
|
|
|
|
|
|
|
|||||||
|
|
|
b |
|
b |
|
b |
|
b |
|
|
||||
|
|
|
∫ xdl |
|
∫ x 1+ ( f ′(x))2 dx |
|
∫ f (x)dl |
|
∫ f (x) 1+ ( f ′(x))2 dx |
|
|
||||
|
x = |
a |
= |
a |
, y = |
a |
= |
a |
|
. |
|
||||
b |
b |
b |
b |
||||||||||||
|
c |
|
|
c |
|
|
|
||||||||
|
|
|
∫ dl |
|
∫ 1+ ( f ′(x))2 dx |
|
∫ dl |
|
∫ 1+ ( f ′(x))2 dx |
|
|
||||
|
|
|
a |
|
a |
|
a |
|
a |
|
|
||||
Consider the area of the region bounded by y = f (x) , and the x- axis from
x = a to x = b, as shown in fig. 2.5. The centroid of this region is defined as the point (xc, yc), where
168

|
|
b |
|
|
|
1 |
b |
|
|
|
∫ xf (x)dx |
|
|
|
∫ f 2 (x)dx |
|
|
|
|
|
|
|
2 |
|
||
x |
= |
a |
, |
y = |
|
a |
. |
|
|
|
|||||||
b |
|
|
b |
|||||
c |
|
|
c |
|
|
|||
|
|
∫ f (x)dx |
|
|
|
|
∫ f (x)dx |
|
|
|
a |
|
|
|
|
a |
|
Т.8 Typical problems
Area
1. Find the area of the region bounded by the curve y = x 2 − 3x and the line
y = 4.
Solution. A sketch of the region is given in fig. 2.14. To determine where the curves intersect we solve the system formed by the equations y = x 2 − 3x and
y = 4. We obtain y = x2 − 3x |
x1 = −1; x2 = 4; |
y = 4 |
y1 = 4; y2 = 4. |
Thus the curve and the line intersect at (-1; 4) and (4; 4). The height is the y- value on the upper line minus the y-value on the lower curve:
4 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
y |
|
|
S = ∫[4 − (x 2 − 3x)]dx = ∫[4 − x 2 |
+ 3x]dx = |
4 |
|
|
||||||||||||||||||
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
x |
3 |
|
|
|
3 |
|
2 |
|
|
|
64 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= 4x − |
|
|
|
+ |
|
|
x |
|
|
= 16 − |
|
+ 24 |
− |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–1 |
3 4 x |
|||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
5 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
– |
|
|
|
|
|
|
|
3 |
|
. |
|
|
|
|
|
|
|
|||||
−4 |
+ |
|
|
+ |
|
|
|
= 20 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
2 |
|
6 |
|
|
|
|
|
|
Fig. 2.14 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
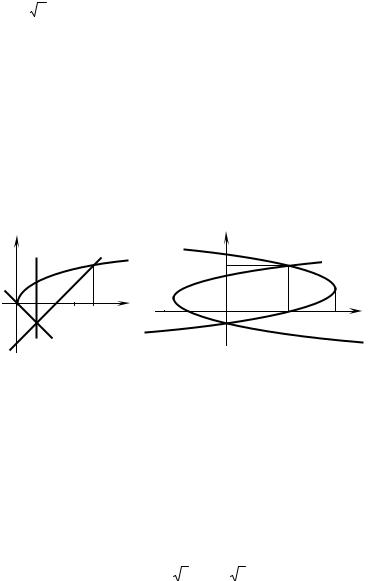
2. Find the area of the region bounded by the curve |
y = |
|
x and the lines |
|||||||||||||||||
y = x − 2 , y = − x (see fig. 2.15 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Solution. The line x = 1 |
is passed through the intersection of the straight |
|||||||||||||||||||
lines y = x − 2 and |
y = − x , |
and is |
divids |
the region by two parts. Then |
||||||||||||||||
S = S1 + S2 , where S |
is the given region, |
|
S1 |
is the left part and is bounded by |
||||||||||||||||
the lines y = − x , x = 1 and the curve |
y = |
|
|
x , |
S2 |
is the right part of S and is |
||||||||||||||
bounded by the lines y = x − 2 , x = 1 and |
|
y = |
|
x . We have: |
|
|
||||||||||||||
1 |
|
|
|
3 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
S1 = ∫ |
|
2x |
2 |
|
|
|
|
x 2 |
|
|
|
2 |
|
1 |
|
5 |
|
|||
( x + x)dx = |
|
|
|
|
+ |
|
|
|
|
= |
|
|
+ |
|
= |
|
; |
|||
|
3 |
|
|
2 |
|
3 |
2 |
6 |
||||||||||||
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
169 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4 |
|
3 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x |
2 |
|
|
x 2 |
|
|
|
16 |
|
2 |
|
1 |
|
|
19 |
|
||
S2 = ∫ ( x − x + 2)dx = |
|
|
|
− |
|
+ 2x |
|
= |
|
|
− 8 + 8 − ( |
|
− |
|
+ 2) |
= |
|
|
; |
|
3 |
|
2 |
|
3 |
3 |
2 |
6 |
|||||||||||||
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
S = S1 + S2 = |
5 |
+ |
19 |
= 4 . |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
x = y 2 − 2 y − 3 |
||||||
3. Find the area of the region bounded by the two parabolas |
|
||||||||||||||||||||||||||||
and x = 5 + 4 y − y 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Solution. Transforming the |
equations |
we |
get x + 4 = ( y − 1)2 |
and |
|||||||||||||||||||||||||
− (x − 9) = ( y − 2)2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
The |
region is |
sketched |
in |
fig. |
2.16. |
|
|
The |
|
curves |
intersect |
when |
|||||||||||||||||
y 2 − 2 y − 3 = 5 + 4 y − y 2 . Thus |
y 2 − 3y − 4 = 0 , or equivalently (y + 1)(y –4) = 0, |
||||||||||||||||||||||||||||
from which y A = −1 or |
yB = 4 . With vertical strips three integrals are needed |
||||||||||||||||||||||||||||
to evaluate the area. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
у |
х=1 |
у=х–2 |
|
|
|
|
|
|
у |
|
|
|
В |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
х=5+4у–у2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
О |
|
|
|
|
2 |
4 |
х |
–4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 х |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
–2 |
|
|
|
|
у= –х |
|
|
|
|
|
|
|
–1 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Fig. 2.15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fig. 2.16 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Perhaps the use of horizontal strips can simplify our work. So, the total area is given by
4 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
S = ∫[5 + 4y − y 2 − ( y 2 − 2y − 3)]dy = ∫[8 + 6y − 2 y 2 ]dy = |
|
||||||||||||||||
−1 |
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
= 8y + 3y |
2 |
|
2 y3 |
|
|
4 |
32 + 48 − |
128 |
− (−8 + 3 + |
2 |
) = |
125 |
|
|
|||
|
|
|
|
||||||||||||||
− |
|
|
|
= |
|
. |
|||||||||||
|
3 |
|
|
− |
|
3 |
3 |
|
3 |
|
|||||||
|
|
|
|
|
1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4. Find the area |
of the less |
region bounded by the |
ellipse x = 6 cos t , |
||||||||||||||
y = 4 sin t and the straight line |
y = 2 3 ( y ≥ 2 |
3 ) . |
|
|
|
|
|
|
|||||||||
Solution. The region is sketched in fig. 2.17. The given area S is equal to
S = 2SMNC = 2(SONCD − SOMCD ) .
170

 Answers
Answers α
α