
Higher_Mathematics_Part_2
.pdf
In this case a1 = grad u(M1 ) , a2 = grad u(M2 ) . We have
∂u = |
|
1 |
|
|
|
|
y , |
|
|
∂u |
= |
|
1 x |
, |
|
∂u |
= − 1 |
|
xy , |
||||||||||||||||
∂x |
2z x |
|
|
∂y |
|
|
2z y |
|
|
|
|
∂z |
|
|
z 2 |
|
|
||||||||||||||||||
a = |
1 |
i + |
1 |
|
j − 2k |
, |
|
|
|
a = − |
1 |
i − |
1 |
j − k ; |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
1 |
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
− |
|
|
|
+ |
|
|
|
|
|
− |
|
|
|
|
− 2 (−1) |
|
|
|||||||||
|
|
|
|
|
|
2 |
2 |
2 |
|
|
|
1 |
|
||||||||||||||||||||||
cos ϕ = |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
= |
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
+ |
1 |
|
+ 4 |
|
1 |
|
+ |
1 |
+ 1 |
|
|
3 |
|||||||||||
Since |
|
|
|
|
|
|
|
|
|
4 |
4 |
|
4 |
|
4 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 . |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ = arccos |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
5. Examine z = x2 − 2y3 − 2x + 6y for relative extrema. |
|
||||||||||||||||||||||||||||||||||
Solution. If we set |
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
= 2x − 2 and |
|
|
|
= −6y 2 + 6 , |
|
|
|||||||||||||||||||||||||
|
|
|
|
∂x |
|
∂y |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Then according to (2.11) we will have |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2x − 2 = 0, |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
+ 6 = 0. |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
− 6y |
|
|
|
|
|
|
|
|
|
|
||||||||||||
This gives x1,2 = 1 and y1,2 = ± 1. Thus M1 (1; 1) |
and M 2 (1; − 1) are the |
||||||||||||||||||||||||||||||||||
critical points.
Now we apply the second-derivative test. Finding the partial derivatives of the second order for the given function:
|
∂ 2 z |
= 2 |
, |
|
∂ 2 z |
= 0 , |
|
∂ |
2 z |
|
= −12 y . |
|
∂x2 |
|
∂x∂y |
|
∂y 2 |
|
|||||
|
|
|
|
|
|
|
|
||||
At M1 (1; 1) , |
|
|
|
|
|
= 2 (−12) − 0 = −24 < 0 . |
|||||
|
A = 2 , B = 0 , |
C = −12 , |
|||||||||
Since |
< 0 , there is no relative extremum at M1 (1; 1) . |
||||||||||
|
|
|
|
At M 2 (1; − 1) , |
|
|
|||||
|
A = 2 , B = 0 , C = 12 , |
|
= 24 > 0 . |
||||||||
Since |
> 0 and A > 0 , there is a relative minimum at M 2 (1; − 1) . The |
||||||||||
minimum output is obtained when x = 1 and y = - 1. At this point the value of the
function is zmin |
= z(1; −1) = −3 . |
6. Examine |
z = x3 + xy 2 + x2 y for relative extrema. |
|
41 |

Solution. Solving
∂z∂x∂z∂y
= 3x2 + y2 + 2xy = 0,
= 2xy + x2 = 0,
we get the critical point M (0; 0) . Now
∂ 2 z |
= 6x + 2y , |
∂ 2 z |
= 2y + 2x , |
∂ 2 z |
= 2x . |
|||
∂x2 |
∂x∂y |
∂y |
2 |
|||||
|
|
|
|
|||||
At M (0; 0) all the second-order |
derivatives are zero, hence |
|||||||
A = B = C = = 0 and the second-derivative test gives no information. However at M (0; 0) the value of the function is z(0; 0) = 0 .On a straight line y = 0 the
function z = x3 . For all x > 0 |
z(x; |
0) = x3 > 0 , but if |
x < 0 z(x, 0) = x3 < 0 . |
Hence, a nearby point M (0; 0) |
function has positive and negative values. There |
||
is no relative extremum at M. |
|
u = x2 + y 2 + 2z 2 |
|
7. Find the relative extrema of |
subject to the constraint |
||
x − y + z = 1.
Solution. Transforming z, which is a function of three variables, into a function of two variables such that the new function reflects constraint x − y + z = 1. Solving it for z, we get
z = 1− x + y
which when substituted for x in u gives: u = x2 + y 2 + 2(1 − x + y)2 .
Since u is now expressed as a function of two variables, to find relative extrema we follow the usual procedure of setting its partial derivatives equal to 0:
∂∂ux = 2x −4(1−x + y) = 0 ;
x − 2(1− x + y) = 0,y + 2(1− x + y) = 0;
|
∂u = 2y +4(1−x + y) = 0 ; |
|
|
∂y |
|
y = − x, |
x = 2 / 5, |
|
|
5x = 2; |
y = −2 / 5. |
Hence the only critical point of u(x, y) subject to constraint x − y + z = 1 is
|
2 |
|
2 |
|
|
M |
|
; − |
|
. |
|
5 |
5 |
||||
|
|
|
By using the second-derivative test on u = x2 + y 2 + 2(1 − x + y)2 at M, we
have: |
|
|
|
|
|
|
|
|
|
∂ 2u |
= 6 |
; |
∂ 2u |
= −4 |
; |
∂ 2u |
= 6 |
, |
|
∂x2 |
∂x∂y |
∂y 2 |
|||||||
|
|
|
|
|
|
||||
|
|
|
42 |
|
|
|
|
||

(M ) = 6 6 − (−4)2 = 20 > 0 and A = ∂ 2u = 6 > 0 .
∂x2
Computing z = 1 − 52 − 52 = 15 .
Thus the function u = x2 + y2 +2z2 , subject to the constraint, has a relative minimum at point M1 (0, 4; −0, 4; 0, 2) . At this point the value of the function is
umin = u(M1) = 0, 4 . |
z = 3x + 2y3 |
|
|
|
|
|||||||||||
8. Find the relative extrema of |
subject to the constraint that x |
|||||||||||||||
and y must satisfy |
|
x2 |
+ y2 = 1, x ≥ 0. |
|
|
|
|
|
|
|
||||||
|
4 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Solution. Function z can be described parametrically: |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
π |
|
π |
|
|
|||
|
|
|
x = 2 cos t , y = sin t , t − |
|
; |
|
. Then we get |
|
||||||||
|
|
|
2 |
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
z(t) = 6 cos t + 2sin3 t . |
|
||||||||
To examine z(t) for relative extrema: |
|
|
|
|
|
|
|
|||||||||
|
|
|
z′(t) = −6sin t + 6sin 2 t cost = 3sin t(sin 2t − 2) ; |
|
||||||||||||
|
|
|
|
sin t(sin 2t − 2) = 0, sin t = 0, |
|
t = πn, n Z . |
|
|||||||||
|
|
π |
|
π |
|
|
|
|
|
|
|
′ |
||||
For t − |
|
; |
|
|
we have t = 0 |
. It is the only critical point. If t < |
0, then z > |
|||||||||
2 |
2 |
|||||||||||||||
|
|
|
|
z(t) has a relative maximum at |
t = 0 . We |
|||||||||||
0 and if t > 0, then z′ < 0. Hence |
||||||||||||||||
calculate xmax = 2 cos 0 = 2 , ymax = sin 0 = 0 and zmax = 6 . |
|
|||||||||||||||
Thus the function z = 3x + 2 y3 , subject to the constraint |
x2 |
+ y 2 |
= 1, x ≥ 0 , |
|||||||||||||
|
||||||||||||||||
has a relative maximum at (2; 0) . |
|
|
|
|
4 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||
9. Find |
the |
relative extrema of z = 8 − 2x − 4y subject to the |
constraint |
|||||||||||||
x2 + 2y 2 − 12 = 0 .
Solution. The first step is to form a certain function by Lagrange. L = 8 − 2x − 4y + λ(x2 + 2y 2 − 12) ,
Then compute the partial derivatives and find where they are all simultaneously 0:
|
∂L |
= −2 |
+ 2λx = |
0, |
|
|
|
|
|
|
|
|
||
|
∂x |
|
|
λx = 1, |
x |
= 1/ λ, |
||||||||
|
|
|
|
|
|
|||||||||
|
∂L |
= −4 |
+ 4λy = |
0, |
|
|
λy = 1, |
|
|
= 1/ λ, |
||||
|
∂y |
|
|
y |
||||||||||
|
|
|
|
|
|
2 |
+ 2 y |
2 |
= 12; |
|
2 |
= 1/ 4, |
||
|
∂L |
= x2 |
+ 2y2 − 12 |
= |
x |
|
|
λ |
|
|||||
|
∂λ |
0; |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
43 |
|
|
|
|
|
|
|
hence there are |
two critical points |
of z. If λ = 1/ 2 , then |
λ = −1/ 2 , then |
x = y = −2 . Thus at |
M1 (2; 2) and M 2 (−2; − |
relative maximum, a relative minimum, or neither of these. Using the second-derivative test we find d 2 L :
x = y = 2 and if 2) may exists a
|
|
|
|
|
|
∂2 L |
= 2λ ; |
∂2 L |
= 4λ ; |
∂ 2 L |
= 0 ; |
|
|||||||
|
|
|
|
|
|
∂x2 |
∂y2 |
∂x∂y |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
d 2 L = 2λdx2 + 2 0dxdy + 4λdy2 |
= 2λ(dx2 + 2dy2 ) . |
|
||||||||||||||||
If λ = 1/ 2 then d 2 L > 0 , thus at M1 (2; 2) |
there is provide the minimum of |
||||||||||||||||||
z on the |
circle x2 + 2y 2 − 12 = 0 ; if λ = −1/ 2 |
then d 2 L < 0 , namely |
at |
||||||||||||||||
M 2 (−2; − 2) there is provide the maximum of z on the circle. Compute |
|
||||||||||||||||||
|
|
|
|
zmin = z(2; 2) = −4 , zmax = z(−2; − 2) = 20 . |
|
||||||||||||||
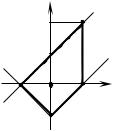
10. Find the largest and smallest values of a function z = x2 + xy + 2 y 2 |
on |
||||||||||||||||||
a polygon D = {(x, y) |
|
x ≤ 1, y ≤ x + 1, y ≥ |
|
x |
|
−1} . |
|
|
|||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
||||||||||||||||
y |
|
|
В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
Solution. Solving |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
D |
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
∂x = 2x + y = 0, |
x = 0, |
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||
–1 М |
|
|
С x |
|
|
∂z |
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
|
= x + 4y = 0 |
y = 0, |
|
|||||||||||||
|
∂y |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
–1 |
К |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Fig. 1.17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
we get the critical point M (0; 0) which lies on D (fig. 1.17).
It is necessary to consider the behavior of z on the boundary of D, which consists of four edges labeled АВ, ВС, СК and КА.
On АВ: y = x + 1, x [−1;1] . Thus, if (x, y) is on AB,
z = x2 + x(x + 1) + 2(x + 1)2 = 4x2 + 5x + 2 .
|
|
5 |
|
|
|
Since x goes from –– 1 to 1 on AB, the minimum of z on AB is at M1 |
|
|
3 |
||
− |
|
, |
|
. |
|
|
|
||||
|
|
|
|
|
|
|
|
8 |
|
8 |
|
On ВС: x = 1, y [0; 2] . Thus, if (x, y) is on BC, |
|
|
|||
|
|
|
|
|
|
z = 1+ y + 2 y2 . |
|
|
|
|
|
The minimum of z is at y = −1/ 4 [0; 2] . In other words, |
we |
will not |
|||
consider M2(1; - 1 ), because it does not lie on BC . |
|
|
|
|
|
4 |
|
|
|
|
|
44 |
|
|
|
|
|
On КС: y = x − 1, x [0;1] . Thus, if (x, y) is on AB,
z = x2 + x(x − 1) + 2(x − 1)2 = 4x2 − 5x + 2 . |
|
|
|
|
Since x goes from 0 to 1 on КС, the minimum of z on КС is at M2( |
5 |
; - |
3 ). |
|
The last, on КА: y = − x − 1, x [−1; 0] . Thus, if (x, y) is on AB, |
8 |
|
8 |
|
|
|
|
||
z = x2 + x(− x − 1) + 2(− x − 1)2 = 2x2 + 3x + 2 . |
|
|
|
|
Since x goes from –– 1 to 0 on КА, the minimum of z on КА is at M3(- |
3 |
; - |
1 ). |
|
4 |
||||
|
|
4 |
Compute values of z(x, y) at points M, M1 , M 2 , M 3 , other at A, B,C and K: z(M ) = 0 , z(M1 ) = 7 /16 , z(M2 ) = 7 /16 , z(M 3 ) = 7 / 8 , z(A) = 1 ,
z(B) = 11 , z(C) = 1, z(K) = 2 .
Namely,
|
|
|
max z(x, y) = z(1; 2) = 11 ; |
min z(x, y) = z(0; 0) = 0 . |
||
|
|
|
|
D |
|
D |
|
|
|
Self-test and class assignments |
|||
|
Т.3 |
|
||||
|
|
|
||||
|
Find the equations of the tangent plane and normal line to the given |
|||||
surface z(x, y) |
at the given point М. |
|
||||
1. |
z = x2 + 3y 2 |
, M (2,1) . |
|
|||
2. |
sin 2 x + sin 2 |
y + cos2 z = 2 , M (π / 2, π / 4, π / 4) . |
||||
3.xyz = e x+ y+ z + 1, M (2,−1,−1) .
4.x2 − 3x + y2 + 2xy + 2xz − 2zy + 2 = z2 , at the cross points with x –– axis.
5. Compute the directional derivative of u = xy 2 + z3 − xyz at M (1; 1; 2)
in the direction of the vector consisting of x- and y-axes, the angles respectively
α = 60° and β = 45° .
6. Compute the directional derivative of |
z = ln(x2 + y 2 ) |
at |
M (2; 1) in the |
||
direction from M to N (6; 4) . |
|
|
|
|
|
7. Compute the directional derivative of |
z = x2 − 3xy + 2y 2 |
at |
M (1; 1) |
in |
|
the direction of its gradient. |
|
|
|
|
|
8. Find a gradient of function u = ze x− y+ 2z at point M (1; 0; 0) . |
|
|
|||
9. Find the points where a gradient of function z = ln(x − y −1 ) |
is equal to |
||||
i + j . |
|
|
|
|
|
10. Find an angle between the gradients of a function |
z = arctg(x / y) |
at |
|||
points M1 (1; 1) and M 2 (−1; − 1) . |
|
|
|
|
|
45 |
|
|
|
|
|

Examine the given functions for relative extrema.
11. |
z = x2 |
− 4xy + 5y 2 − 2x + 10y . |
12. |
z = x3 + 3xy 2 − 15x − 12y . |
13. |
z = x2 |
+ xy + y 2 − 4 ln x − 10 ln y . |
14. |
z = 2x4 + xy3 . |
15. |
z = x |
1 + y + y 1 + x . |
16. |
z = e x2 − y (5 − 2x + y) . |
Find the relative extrema |
of |
the |
given functions u(x, y, z) subject to the |
||||||
given constraint f(x, y) = 0. |
|
|
|
|
|
|
|
|
|
17. |
u = x2 − y 2 , |
if x + 2y − 6 = 0 . |
|||||||
18. |
u = xyz , |
if |
|
x + y + z = 6 . |
|||||
19. |
u = 4x2 + y 2 , |
if |
|
1 |
+ |
|
2 |
− 4 = 0 . |
|
|
|
||||||||
|
|
|
|
x |
|
y |
|
||
20. |
u = xy 2 z 2 , |
if |
|
x + 4y − 2z − 10 = 0 . |
|||||
21. |
u = 16 − 10x − 24y , |
if |
|
x2 + y 2 |
− 169 = 0 . |
||||
22. |
u = 4x2 + 2y 2 + z 2 , |
if |
|
x2 + y 2 |
+ z 2 − 1 = 0 . |
||||
Find the largest and smallest values of the given functions z(x, y) on the given polygons D.
23. |
z = x 2 − xy + y 2 − 3x + 3y , D = {(x, y) |
|
|
|
x ≥ 0, y ≤ 0, x − y ≤ 3} . |
||||||||
|
|||||||||||||
24. |
z = x3 + y3 − 3x − 9 y + 9 , D = {(x, y) |
|
|
|
x |
|
+ |
|
y |
|
≤ 3} . |
||
|
|
|
|
||||||||||
|
|
|
|
||||||||||
25. |
z = 3x2 + 3y 2 − x − y , D = {(x, y) |
|
|
x ≤ 5, y ≥ 0, y ≤ x − 1}. |
|
|
|||||
26. |
z = 2x2 y − x3 y − x2 y 2 , D = {(x, y) |
|
x ≥ 0, y ≥ 0, x + y ≤ 6} . |
||
|
|||||
27. |
z = 4 − 2x2 − y 2 , D = {(x, y) y ≥ 0, y ≤ 1 − x2 } . |
||||
 Answers
Answers
1. |
4x + 6y − z − 7 = 0 , |
x − 2 |
= |
y − 1 |
= |
z − 7 |
. |
|
|
2. y − z = 0 , |
|
|
x − π / 2 |
= |
y − π / 4 |
= |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
6 |
|
|
|
− 1 |
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
||||
= |
z − π / 4 |
. |
3. |
y + z + 2 = 0 , |
|
x − 2 |
= |
y + 1 |
|
= |
z + 1 |
. |
|
4. |
M1(1;0;0), x − y − 2z − 1 = 0, |
|||||||||||||||||||
|
−1 |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x − 1 |
= |
y |
|
= |
z |
; |
M2 (2;0;0), x + 2y + 4z − 2 = 0, |
|
x − 1 |
= |
y |
= |
z |
. 5. 5 або –6. 6. 22 / 25 . |
|||||||||||||||||||
|
|
1 |
|
2 |
|
1 |
|
2 |
4 |
|||||||||||||||||||||||||
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
7. |
2. |
8. |
gradu = ek . |
9. (2; 1), (0; ––1). 10. 180° . |
|
11. (–5;–3) is a point of the |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
46 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

relative minimum. 12. (2; 1) is a point of the relative minimum. (–2; –1) is a point of the relative maximum. 13. (1; 2) is a point of the relative minimum. 17.(–2; 14) –– point of
the relative minimum subject to the constraint. 18. umax = f(2, 2, 2) = 8. 21. (5; 12) is a point of the relative minimum subject to the constraint. (–5; –12) is a point of the relative
maximum subject to the constraint. 23. zmin = f (1; − 1) = −3 , |
zmax = f (0; 0) = 4 . |
||||
24. zmin = f (−3; 0) = −9 , zmax = f (3; 0) = 27 . |
25. |
zmin = f (1/ 6; 1/ 6) = −1/ 6, |
|||
zmax = f (5; |
4) = 114. |
26. zmin = 0, zmax = f (1; 0,5) = 0,25. |
|||
27. zmin = f (1; 0) = f (−1; 0) = 2 , zmax = f (0; |
0) = 4. |
|
|||
|
|
|
Individual tasks |
|
|
|
Т.3 |
|
|
|
|
3.1. Find the equations of the tangent plane and the normal line to the given surface z(x, y) at the given point М.
3.1.1. z = |
x2 + y |
2 |
, |
|
M (2; |
2) . |
3.1.2. z = |
x2 |
− xy + y 2 |
, M (1; 2) . |
|||||||||||||
x3 + y3 |
|
|
|
|
x + y |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3.1.3. z = sin(ex− y − 1) , M (1;1) . |
3.1.4. z = |
|
|
|
x |
|
|
|
, M (2; −1) . |
||||||||||||||
y(x + y) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3.1.5. z = 3 x2 + y2 +10, M (1; 4) . |
3.1.6. z = ln(x2 − y2 − 4), M(3;2). |
||||||||||||||||||||||
3.1.7. z = arctg(ex2−2xy ) , |
M (2; 1) . |
3.1.8. z = ex2 −3xy+ 2 y2 , |
M (1;1) . |
||||||||||||||||||||
3.1.9. z = |
(x − y |
2 |
)e |
x |
2 + y |
, |
M (1; − 1) . |
3.1.10. z = x |
3 |
y |
2 |
+ arctg |
x |
,М(1;1). |
|||||||||
|
|
|
|
|
y |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3.1.11. z = (x2 + y 2 − x)e xy , M (1; 0) . |
3.1.12. z = arctg |
|
x + y |
, М(2;0). |
|||||||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − y |
|
|
|||||
3.1.13. z = x3 −y2 + 3x + 2y , M (1; 2) . |
3.1.14. z = 3 x4 + y4 + 10, (1;2). |
||||||||||||||||||||||
3.1.15. z = 4 x3 − xy + y3 |
, M (1; −1) . |
3.1.16. z = |
x − xy + y |
, |
M (1; 0) . |
||||||||||||||||||
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x2 + y 2 |
|
|
|||||||||
3.1.17. z =
3.1.19. z =
3.1.21. z =
3.1.23. z =
x2 |
+ y 2 |
, M (1;1) . |
3.1.18. z = |
x − y |
, M (1;1) . |
|
x3 |
+ y3 |
x3 + y3 |
||||
|
|
|
||||
e x2 − x− y+ y2 , M (1; 0) . |
3.1.20. z = |
3x2 − y , M (2; 3) . |
||||
ln(2x2 − 7 y2 ) , M (2; 1) . |
3.1.22. z = |
5x2 + 4 y , M (2; −1) . |
||||
x2 + 2 y2 − 2x − 1, M (2; 1) . |
|
|
|
|||
47

3.1.24.z = (x2 + 4xy − y 2 − 3)3 , M (1;1) .
3.1.25.z = xy + x2 + y2 , M (−3; 4) .
3.1.26.z = ln(x2 − 3xy + y 2 + 2) , M (2; 1) .
3.1.27.z = (x + 2 y) x2 + y2 , M (1; 0) .
|
|
|
|
π |
|
π |
|
3.1.28. |
z = arctg(cos x +sin y) , |
M |
|
|
; |
|
. |
3 |
|
||||||
|
|
|
|
6 |
|||
3.1.29. z = 3 x2 + 3xy − 4x + 3y − 1, |
M (1; 2) . |
||||||
3.1.30.z = ln(x2 − 3xy − y − 2) , M (4; 1) .
3.2.Find the angle between the gradient of the given function u and v at the given point М.
3.2.1. |
u = arctg( x / y) , v = ln(x 2 + y ) , M (1;1) . |
3.2.2. |
u = 3x2 + 4y2 + z2 , v = 4 2x + 5y + 3z , M (1;1; 3) . |
3.2.3.u = arcsin(xy) , v = arccos(xy) , M (3;1/ 4) .
3.2.4.u = x3 y + xz 2 + y 2 z , v = xyz + yz 2 , M (1; 0;1) .
Find the angle between the gradient of a function u at points M1 and M2 .
3.2.5.u = xy 2 z 4 , M1 (1; 2;1) , M 2 (1; − 1; 0) .
3.2.6.u = xy z −2 , M1 (4;1;1) , M 2 (1; 9; − 1) .
3.2.7.u = 3 xy + 3 yz + 3 xz , M1 (1; 8;1) , M2 (1; 1; 1) .
3.2.8.u = arctg(x + y2 z) , M1 (1;1;1) , M 2 (0;1; 2) .
Compute the directional derivative of the given functions u at M1 in the direction from M1 to M2 .
3.2.9. u =  x2 + xy + y3 , M1 (1; 0) , M 2 (2;1) .
x2 + xy + y3 , M1 (1; 0) , M 2 (2;1) .
3.2.10.u = ln(x2 − 3x + y2 ) , M1 (3; 1) , M 2 (2; 3) .
3.2.11.u = e x2 y (x + y)2 , M1 (0;1) , M 2 (−1; 2) .
3.2.12. u = sin 2 x cos 2y , M1 (π / 4; π / 3) , M2 (π / 3; 0) .
Compute the directional derivative of u at M1 in the direction of its gradient at M1 .
3.2.13. u = 3 x + y 2 + z3 , M1 (3; 4; 2) .
48
3.2.14. |
u = x2 + y 2 |
(x2 + z 2 )−1/ 2 , M1 (3; 4; − 4) . |
3.2.15. |
u = ln( xy + |
yz ) , M1 (1; 4;1) . |
3.2.16. u = arcctg(xy2 z) , M1 (1; − 1; 2) .
Find gradu and | gradu | of u at М.
3.2.17. u = xy 2 z −3 +  x ( yz)−1 , M (1; − 2; 2) .
x ( yz)−1 , M (1; − 2; 2) .
3.2.18. u = xyz + x2 + y 2 + z 2 − 2 , M (1; 4;1) .
3.2.19.u = ln(x3 + y3 + z3 ) , M (1; − 1; 2) .
3.2.20.u = x2 + y2 + z2 , M (6; −2; 3) . Find the points where gradu = a .
3.2.21.u = x2 + xy + yz + xz , a = 5i + 3 j + 2k .
3.2.22.u = x2 + y 2 + z 2 + 3xy + 2y + xz , a = −i + 4k .
3.2.23. u = |
x3 |
+ xy 2 + z 2 , a = 4i + 4 j − k . |
|
||
3 |
|
|
3.2.24.u = x2 + 2 y2 − z2 − xy + 2x − 4z , a = 5i + 2 j . Find the points where | gradu |= b .
3.2.25.u = ln(x2 + y 2 ) , b = 2 .
3.2.26.u = arctg xy , b = 3 .
3.2.27.u = x + 2y , b = 1 .
Find the directional derivative of u at M in the direction of its radius-vector.
3.2.28. u = arcsin |
x |
, M (1;1; 2) . |
|
yz |
|
3.2.29.u = x2 + y2 + z2 , M (1; 2; − 2) .
3.2.30.u = ln sin(x + 2yz) , M (0; π / 6;1) .
3.3. Examine the given functions for relative extrema.
3.3.1. z = 4x + |
y 2 |
+ 2y + y 2 . |
3.3.2. |
z = ln(xy) + |
1 |
+ |
2 |
. |
|
x |
|
|
|
x |
|
y |
|
3.3.3. z = x2 + 8xy + 20y2 − 20y . |
3.3.4. z = 3 + 6x − x2 − xy − y2 . |
|||||||
|
|
|
49 |
|
|
|
|
|

3.3.5. z = ln(x4 y) + |
1 |
+ |
1 |
− 3x . |
||
|
|
|||||
|
|
|
x |
y |
||
3.3.7. z = 9x + |
y 2 |
+ 6y + 3y 2 + 2 . |
||||
|
||||||
|
x |
|
|
|||
3.3.9. z = 27x3 + 18xy2 − 153x − 72y . |
||||||
3.3.11. |
z = x4 + y 4 − 2x2 + 4xy − 2y 2 . |
|
3.3.13. |
z = e− x2 − y2 (2x2 + y2 ) . |
|
3.3.15. |
z = x2 + xy + y2 − 6x − 9 y . |
|
3.3.17. |
z = x2 + 5y 2 + 2x + 4xy − 6 y . |
|
3.3.19. |
z = y |
x − 2y 2 − x + 14y . |
3.3.21. |
z = 2y |
3x − 8y 2 − 3x + 28y . |
3.3.23. |
z = (x + y) ln(x + y) + x2 . |
|
3.3.25. |
z = (x + 2 y) ln(x + 2y) + 4y 2 |
|
3.3.27. |
z = x3 + y3 − 3xy2 − 9x + 9 y . |
|
3.3.19. |
z = (x − 2) y + 1 − x2 + 4x − y . |
|
3.3.6. z = ln(xy2 ) + 5y + 6x . xy
3.3.8. z = 2x − y + y + ln x + 1 . x
3.3.10. z = 3(x − 1)(x + y) + y2 . 3.3.12. z = x(x + y + 1) + 3y2 . 3.3.14. z = 6x − x2 − xy − y2 .
3.3.16. z = ln(x |
2 y) + |
4 y + 3x |
. |
||||
|
|
||||||
|
|
|
|
|
|
xy |
|
3.3.18. |
z = |
x2 |
− x − |
1 |
− 2y . |
||
4 y3 |
|
y |
|||||
|
|
|
|
|
|
||
3.3.20.z = 9x + ( y − 1)2 + 3y2 .
x− 1
3.3.22.z = x3 + 8y3 − 6xy + 3 .
3.3.24.z = xy(6 − x − y) .
3.3.26.z = 27x3 + 8y3 − 18xy .
3.3.28.z = x y − x2 − y + 6x .
3.3.30.z = 1 + 2y − x2 − 2x . y y3
3.4. Find the largest and smallest values of the given functions z(x, y) on the given polygons D .
3.4.1. z = 3x2 + y2 − 2xy − 4x, |
, |
|
|
|
|
|
|
|
= {(x, y) |
|
−1 ≤ x ≤ 2, − 1 ≤ y ≤ x + 1} . |
|||||||||||||||||||||
D |
|
|||||||||||||||||||||||||||||||
3.4.2. z = x3 − 12xy + y3 , |
|
|
= {(x, y) |
|
0 ≤ x ≤ 4, 0 ≤ y ≤ 2} . |
|||||||||||||||||||||||||||
D |
|
|||||||||||||||||||||||||||||||
3.4.3. z = x2 − 2xy − y2 + 4x , |
|
|
|
|
|
= {(x, y) |
|
|
|
y ≥ 0, x ≥ −3, x + y ≤ −1} . |
||||||||||||||||||||||
|
D |
|
||||||||||||||||||||||||||||||
3.4.4. z = xy(3 − x − y) , |
|
= {(x, y) |
|
x ≥ 0, y ≥ −2, x + y ≤ 6} . |
||||||||||||||||||||||||||||
D |
|
|||||||||||||||||||||||||||||||
3.4.5. z = x3 |
+ 3y 2 , |
|
|
|
|
|
x2 + y 2 ≤ 4} . |
|
||||||||||||||||||||||||
|
= {(x, y) |
|
|
|||||||||||||||||||||||||||||
D |
|
|||||||||||||||||||||||||||||||
3.4.6. z = x2 |
− y2 + 3xy − 5x − y, |
|
|
|
= {(x, y) |
|
x ≤ 3, |
y ≤ 2, 2x + y ≥ 0} . |
||||||||||||||||||||||||
|
|
D |
|
|||||||||||||||||||||||||||||
3.4.7. z = x2 |
+ 2xy − y 2 − 4x , |
|
|
|
|
={(x, y) |
|
x ≤3, |
y ≥0, y ≤ x +1} . |
|||||||||||||||||||||||
|
|
D |
|
|||||||||||||||||||||||||||||
3.4.8. z = (x − y)2 + y 2 + 2x , |
|
= {(x, y) |
|
x ≤ 0, y ≤ 0, x + y + 4 ≥ 0} . |
||||||||||||||||||||||||||||
D |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
