
II_Semestr_PM_M_Zaoch (2)
.pdf
0, |
если x 0; |
0,027, |
если0 x 1; |
|
|
|
если1 x 2; |
F(x) 0,027 0,189 0,216, |
|
0,216 0,441 0,657, |
если2 x 3; |
|
|
|
если x 3. |
0,657 0,343 1, |
Найдём математическое ожидание (все числовые данные записаны в таблице закона распределения) по определению, используя формулу (3):
M(X) 0 0,027 1 0,189 2 0,441 3 0,343 2,1.
Найдём математическое ожидание по формуле (8):
M(X) np 3 0,7 2,1.
Найдём дисперсию по определению, используя формулу (5.1):
n
D(X) xi2 pi [M(X)]2
i 1
02 0,027 12 0,189 22 0,441 32 0,343 (2,1)2 0,63
и по формуле (8)
D(X) npq 3 0,7 0,3 0,63.
Найдём среднее квадратическое отклонение:
(X) 
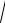 0,63 0,79.
0,63 0,79.
Найдём вероятности (I способ)
P(X 1) P(X 0) 0,027,
P(X 2) P(X 2) P(X 3) 0,441 0,343 0,784.
Найдём вероятности (II способ)
def
P(X 1) F(1) 0,027,
def
P(X 2) 1 P(X 2) 1 F(2) 1 0,216 0,784.
Найдём моду. Так как мода Mo(X) – это значение случайной величины, имеющее наибольшую вероятность, из таблицы закона распределения получаем Mo(X) 2.
Ответ: закон распределения числа верно решённых задач:
Х |
0 |
1 |
2 |
3 |
Р |
0,027 |
0,189 |
0,441 |
0,343 |
Функция распределения
21

0, если x 0;
0,027, если0 x 1;
F(x) 0,216, если1 x 2;
0,657, если 2 x 3;
1, если x 3.
Математическое ожидание: M(X) 2,1. Дисперсия: D(X) 0,63.
Среднее квадратическое отклонение: (X) 0,79. Мода Mo(X) 2.
Пример 2. (Гипергеометрическое распределение). В партии из 10 дета-
лей имеется 8 стандартных. Из этой партии наудачу берут 2 детали. Случайная величина Х – число стандартных деталей среди отобранных. Найдите закон распределения указанной дискретной случайной величины (СВ) Х и её функцию распределения F(x). Вычислите математическое ожидание M(X) дисперсию D(X) и среднее квадратическое отклонение(X). Найдите вероятность P(X<1), вероятность P(X 2) и моду Mo(X).
Решение. Случайная величина Х – число стандартных деталей среди отобранных – имеет гипергеометрический закон распределения. Эта величина может принимать три значения: x1=0 (среди отобранных деталей нет стандартных), x2=1 (среди отобранных деталей одна стандартная), x3=2 (2 детали стандартны). Вычислим вероятности этих значений по формуле (9):
|
|
C0 |
C2 |
1 |
|
|
|
C1 |
C1 |
16 |
|||
p |
P(X 0) |
8 |
2 |
|
|
, |
p |
P(X 1) |
8 |
2 |
|
|
, |
|
|
|
|
|
|
||||||||
0 |
|
C102 |
45 |
1 |
|
C102 |
45 |
||||||
|
|
|
|
||||||||||
p2 P(X 2) C82 2C20 28. C10 45
Следовательно, гипергеометрический закон распределения данной случайной величины можно задать таблицей
Х |
0 |
1 |
2 |
Р |
1/45 |
16/ 45 |
28/45 |
Контроль: 1/45 16/45 28/45 1.
Найдём функцию распределения по формуле (2):
0, |
|
|
|
|
|
|
если x 0; |
||
|
1 |
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
если 0 x 1; |
|
|
|
|
|
|
|
|||
45 |
|
|
|
|
|
|
|
||
|
1 |
|
16 |
|
17 |
|
|
||
F(x) |
|
|
, |
если1 x 2; |
|||||
|
|
|
|
|
|
||||
|
|
|
|
||||||
45 |
45 |
45 |
|
||||||
|
1 |
|
16 |
|
28 |
|
|
||
|
|
|
1, |
если x 2. |
|||||
|
|
|
|
|
|
||||
|
|
|
45 |
||||||
45 |
45 |
|
|
||||||
22

Найдём математическое ожидание по определению, используя формулу
(3) (все числовые данные записаны в таблице закона распределения):
M(X) 0 1 1 16 2 28 1,6. 45 45 45
Найдём математическое ожидание по формуле (10), где N=10, M=8, n=2:
M(X) n |
M |
2 |
8 |
1,6. |
N |
|
|||
|
10 |
|
||
Найдём дисперсию по определению, используя формулу (5.1):
n |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
16 |
|
|
|
|
28 |
|
|
|
|
||
D(X) xi |
2 pi |
[M(X)]2 02 |
12 |
|
|
22 |
|
(1,6)2 |
0,28. |
||||||||||||||||
45 |
|
|
|
||||||||||||||||||||||
i 1 |
|
|
|
|
|
|
|
|
|
|
|
45 |
|
|
|
45 |
|
|
|
|
|||||
Найдём дисперсию по формуле (10): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
D(x) n |
M |
|
|
M |
n |
8 |
|
|
|
8 |
2 |
|
|
|
|||||||||||
|
|
1 |
|
1 |
|
|
2 |
|
|
1 |
|
|
1 |
|
|
0,28. |
|||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
N 1 |
N |
N |
|
|
9 |
10 |
|
10 |
|
|
|||||||||||||
Найдём среднее квадратическое отклонение по формуле (6):
(X) 
 0,28 0,53.
0,28 0,53.
Найдём вероятности
P(X 1) P(X 0) 1 , 45
P(X 2) P(X 2) 28/45.
Найдём моду. Так как мода Mo(X) – это значение случайной величины, имеющее наибольшую вероятность, из таблицы закона распределения получаем
Mo(X) 2.
Ответ: закон распределения числа стандартных деталей среди двух отобранных:
Х |
|
0 |
|
1 |
|
2 |
|
||
Р |
|
1 |
|
|
16 |
|
|
28 |
|
|
45 |
|
45 |
|
45 |
|
|||
|
|
|
|
|
|||||
Функция распределения
0, |
если x 0, |
|
|
если0 |
x 1, |
1/45, |
||
F(x) |
если1 |
x 2, |
17/45, |
||
|
если x 2. |
|
1, |
||
Математическое ожидание: M(X) 1,6.
23

Дисперсия: D(X) 0,28.
Среднее квадратическое отклонение: (X) 0,53.
P(X 1)=1/45, |
P(X 2) 28/45. |
Мода Mo(X) 2 .
Пример 3 (Множество элементарных исходов). Абитуриент сдаёт два вступительных экзамена: по математике и физике. Вероятность получения пятёрки по математике равна 0,8, по физике – 0,6. Случайная величина Х – число полученных на экзаменах пятёрок. Найдите закон распределения указанной дискретной случайной величины (СВ) Х и её функцию распределения F(x). Вычислите математическое ожидание M(X) дисперсию D(X) и среднее квадратическое отклонение (X). Найдите вероятность P(X<1), вероятность P(X 2) и моду Mo(X).
Решение. Найдём сначала закон распределения данной СВ Х. Эта величина может принимать три значения: x1=0 (ни одной пятёрки на вступительных экзаменах), x2=1 (одна пятёрка), x3=2 (две пятёрки).
Пусть событие А состоит в том, что по математике получена пятёрка (P(A) 0,8), событие В – по физике получена пятёрка (P(B) 0,6). Оче-
видно, P(A) 1 0,8 0,2, P(B) 1 0,6 0,4. Тогда вероятность значения
х1 может быть вычислена как вероятность произведения событий A B. Так как А и В – независимые события, то
p P(X 0) P(ни одной пятёрки) Р( A B ) P(A) P(B) 0,2 0,4 0,08. |
||||||||||||
1 |
|
|
|
|
|
|
|
|
||||
Вероятность значения х2 |
|
|
|
|
независ. |
|||||||
может быть вычислена как вероятность суммы |
||||||||||||
несовместных событий |
|
B A |
|
|
, поэтому |
|||||||
A |
B |
|||||||||||
p2 P(X 1) |
P(одна пятёрка) P( |
|
B A |
|
) |
|||||||
A |
B |
|||||||||||
P( |
|
B) P(A |
|
) 0,8 0,4 0,2 0,6 0,44. |
||||||||
A |
B |
|||||||||||
Вероятность значения х3 – это вероятность события A B: |
||||||||||||
p3 P(X 2) P(две пятёрки) P(A B) P(A) P(B) 0,8 0,6 0,48.
Следовательно, закон распределения данной случайной величины можно задать таблицей
Х |
0 |
1 |
2 |
Р |
0,08 |
0,44 |
0,48 |
Контроль: 0,08+0,44+0,48=1.
Найдем функцию распределения по формуле (2):
24
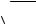
0, |
если x 0; |
|
если0 x 1; |
0,08, |
|
F(x) |
если1 x 2; |
0,08 0,44 0,52, |
|
0,08 0,44 0,048 1, |
если x 2. |
|
|
Найдём математическое ожидание, используя формулу (3) (все числовые данные записаны в таблице закона распределения):
M(X) 0 0,08 1 0,44 2 0,48 1,4.
Найдём дисперсию, используя формулу (5.1):
n
D(X) xi2 pi [M(X)]2
i1
02 0,08 12 0,44 22 0,48 (1,4)2 0,4.
Найдём среднее квадратическое отклонение:
(X) 
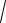 0,4 0,63.
0,4 0,63.
Найдём вероятности
P(X 1) P(X 0) 0,08,
P(X 2) P(X 2) 0,48.
Найдём моду. Так как мода Mo(X) – это значение случайной величины, имеющее наибольшую вероятность, из таблицы закона распределения получаем
Mo(X) 2.
Ответ: закон распределения числа полученных на двух экзаменах пятерок:
|
|
Х |
|
|
0 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
Функция |
рас- |
Р |
|
|
0,08 |
|
0,44 |
0,48 |
пределения |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
0, |
если x 0; |
|||
|
|
|
|
|
|
если 0 x 1; |
|||
|
|
|
F |
|
0,08, |
||||
|
|
|
(x) |
если1 x 2; |
|||||
|
|
|
|
|
0,52, |
||||
|
|
|
|
|
1, |
если x 2. |
|||
|
|
|
|
|
|
|
|
|
|
Математическое ожидание: M(X) 1,4. |
|
|
|||||||
Дисперсия: |
D(X) 0,4. |
|
|
|
|
|
|
||
Среднее квадратическое отклонение: |
(X) 0,63. |
||||||||
P(X 1) 0,08, |
P(X 2) 0,48. |
|
|
||||||
Мода Mo(X) 2.
25
5. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ
Задание №5
1.Валик, изготовленный автоматом, считается стандартным, если отклонение его диаметра от проектного размера не превышает 2 мм. Случайные отклонения диаметра валиков подчиняются нормальному закону со средним квадратическим отклонением 1.5 мм и математическим ожиданием, равным 0. Сколько стандартных валиков (в %) изготавливает автомат?
2.При определении расстояния радиолокатором случайные ошибки распределяются по нормальному закону. Какова вероятность того, что ошибка при определении расстояния не превосходит 20 м, если извест-
но, что систематических ошибок радиолокатор не допускает, а дисперсия ошибок равна 1370 м2?
3.Детали, выпускаемые цехом, имеют диаметры, распределенные по
нормальному закону с математическим ожиданием, равным 5 см, и дисперсией, равной 0.81 см2. Найдите вероятность того, что диаметр наугад взятой детали – от 4 до 7 см.
4.Случайная величина Х подчинена нормальному закону с математическим ожиданием, равным 0. Вероятность попадания этой случайной величины в интервал (-1;1) равна 0.5. Найдите среднее квадратическое отклонение и записать закон распределения данной случайной величины.
5.Диаметр подшипников, изготовленных на заводе, представляет собой случайную величину, распределенную нормально с математическим ожиданием 1.5 см и средним квадратическим отклонением 0.04 см. Найдите вероятность того, что размер наугад взятого подшипника колеблется от 1 до 2 см.
6.Считается, что отклонение длины изготавливаемых деталей от стандартных является случайной величиной, распределенной по нормальному закону. Зная, что длина стандартной детали 40 см, а среднее квадратическое отклонение 0.4 см, определить, какую точность длины изделия можно гарантировать с вероятностью 0.8?
7.Рост мужчины является случайной величиной, распределенной по
нормальному закону с математическим ожиданием, равным 170 см, и дисперсией, равной 49 см2. Найдите вероятность того, что трое наугад выбранных мужчин будут иметь рост от 170 до 175 см.
26
8.Случайная величина Х распределена нормально с математическим ожиданием 40 и дисперсией 100. Вычислить вероятность попадания случайной величины Х в интервал (30;80).
9.Считается, что изделие – высшего качества, если отклонение его размеров от номинальных не превосходит по абсолютной величине 3.66 мм. Случайные отклонения размера изделия от номинального подчиняется нормальному закону со средним квадратическим отклонением, равным 3 мм. Систематические отклонения отсутствуют. Определить среднее число изделий высшего качества среди 100 изготовленных.
10.Из пункта С ведется стрельба из орудия вдоль прямой СК. Предполагается, что дальность полета распределена нормально с математическим ожиданием 1000 м и средним квадратическим отклонением 5 м. Определить (в %), сколько снарядов упадет с перелетом от 5 до 70 м.
Выполнение типового варианта (задание №5)
Пример 1. Масса пойманной рыбы подчиняется нормальному закону распределения с математическим ожиданием 375 г и средним квадратическим отклонением 25 г. Найдите вероятность того, что масса одной рыбы будет от 300 до 425 г.
Решение. Обозначим через случайную величину Х – массу пойманной рыбы. По условию, Х распределена нормально. Известно, что вероятность попадания значений нормальной случайной величины Х в интервал ( , ) определяется формулой
|
|
|
a |
|
|
a |
||||||
P( X ) |
|
|
|
|
|
|
|
|
, |
|||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
где (x) – функция Лапласа: |
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
x |
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(x) |
|
|
|
e 2 dt, |
|
|
||||||
|
|
|
|
|
|
|||||||
2 |
|
|
||||||||||
|
|
0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
а – математическое ожидание, – среднее квадратическое отклонение случайной величины Х. Для нахождения значений функции (x) существуют специальные таблицы, причем
1.( x) (x), т.е. функция Лапласа нечетная;
2.(x) 0.5, если | x| 5.
По условию задачи а=375, =25, =300, =425, поэтому
27

|
425 375 |
|
300 375 |
|
|
||
P(300 X 425) |
|
|
|
|
|
|
|
25 |
25 |
|
|||||
|
|
|
|
|
|
||
(2) ( 3) (2) (3) 0.4772 0.49865 0.9759.
Ответ: Р(«масса пойманной рыбы будет в пределах от 300 г до 425
г») 0,98.
Пример 2. Автомат изготавливает подшипники. Подшипник считается годными, если отклонение его размера от проектного не превышает 0.77 мм. Случайные отклонения размера подшипников подчиняются нормальному закону распределения со средним квадратическим отклонением 0.4 мм и математическим ожиданием, равным 0. Сколько стандартных подшипников (в %) изготавливает автомат?
Решение. Вероятность того, что абсолютная величина отклонения меньше положительного числа , вычисляется по формуле
P(| X a | ) 2 .
Положив =0.77, а=0, =0.4, находим
0.77
P(| X 0| 0.77) 2 2 (1.93) 2 0.4732 0.9464.0.4
Следовательно, примерно 95 подшипников из 100 окажутся стандартными.
Ответ. Автомат изготавливает в среднем 95% стандартных подшипников.
28
6. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Задание №6
В результате эксперимента получены данные, записанные в виде статистического ряда. Требуется обработать данные в указанных столбцах, а именно:
а) запишите значения результатов эксперимента в виде вариационного ряда;
б) найдите размах варьирования и разбейте его на 9 интервалов;
в) постройте полигон частот, гистограмму относительных частот и график эмпирической функции распределения.
1.Обработать данные в столбцах №1, №3, №5, №7, №9, №10.
2.Обработать данные в столбцах №2, №4, №6, №8, №9, №10.
3.Обработать данные в столбцах №1, №2, №5, №6, №8, №9.
4.Обработать данные в столбцах №2, №4, №5, №7, №8, №10.
5.Обработать данные в столбцах №3, №4, №5, №6, №9, №10.
6.Обработать данные в столбцах №3, №5, №7, №8, №9, №10.
7.Обработать данные в столбцах №4, №5, №6, №7, №9, №10.
8.Обработать данные в столбцах №4, №6, №7, №8, №9, №10.
9.Обработать данные в столбцах №5, №6, №7, №8, №9, №10.
10.Обработать данные в столбцах №1, №2, №3, №4, №5, №6.
№1 |
№2 |
№3 |
№4 |
№5 |
№6 |
№7 |
№8 |
№9 |
№10 |
|
|
|
|
|
|
|
|
|
|
189 |
207 |
213 |
208 |
186 |
210 |
198 |
219 |
231 |
227 |
|
|
|
|
|
|
|
|
|
|
202 |
211 |
220 |
236 |
227 |
220 |
210 |
183 |
213 |
190 |
|
|
|
|
|
|
|
|
|
|
197 |
227 |
187 |
226 |
213 |
191 |
209 |
196 |
202 |
235 |
|
|
|
|
|
|
|
|
|
|
211 |
214 |
220 |
195 |
182 |
228 |
202 |
207 |
192 |
226 |
|
|
|
|
|
|
|
|
|
|
193 |
203 |
232 |
202 |
215 |
195 |
220 |
233 |
214 |
185 |
|
|
|
|
|
|
|
|
|
|
234 |
215 |
196 |
220 |
203 |
236 |
225 |
221 |
193 |
215 |
|
|
|
|
|
|
|
|
|
|
29
204 |
184 |
217 |
193 |
216 |
205 |
197 |
203 |
229 |
204 |
|
|
|
|
|
|
|
|
|
|
225 |
216 |
233 |
223 |
208 |
204 |
207 |
182 |
216 |
191 |
|
|
|
|
|
|
|
|
|
|
210 |
190 |
207 |
205 |
232 |
222 |
198 |
217 |
211 |
201 |
|
|
|
|
|
|
|
|
|
|
185 |
217 |
225 |
201 |
208 |
211 |
189 |
205 |
207 |
199 |
|
|
|
|
|
|
|
|
|
|
Выполнение типового варианта (задача №6)
В результате эксперимента получены данные, записанные в виде статистического ряда:
22 |
26 |
32 |
34 |
26 |
28 |
|
|
|
|
|
|
30 |
28 |
18 |
22 |
24 |
26 |
|
|
|
|
|
|
34 |
24 |
28 |
20 |
32 |
17 |
|
|
|
|
|
|
30 |
22 |
26 |
35 |
28 |
24 |
|
|
|
|
|
|
20 |
30 |
17 |
24 |
32 |
28 |
|
|
|
|
|
|
34 |
26 |
24 |
28 |
22 |
30 |
|
|
|
|
|
|
28 |
22 |
36 |
30 |
20 |
26 |
|
|
|
|
|
|
20 |
26 |
30 |
24 |
32 |
17 |
|
|
|
|
|
|
28 |
35 |
32 |
22 |
26 |
24 |
|
|
|
|
|
|
18 |
24 |
26 |
28 |
35 |
30 |
|
|
|
|
|
|
а). Запишите значения результатов эксперимента в виде вариационного ряда;
б). Найдите размах варьирования и разбейте его на 9 интервалов;
в). Постройте полигон частот, гистограмму относительных частот и график эмпирической функции распределения.
Решение. а). Располагаем значения результатов эксперимента в порядке возрастания, т.е. записываем вариационный ряд:
17 |
17 |
17 |
18 |
18 |
20 |
|
|
|
|
|
|
20 |
20 |
20 |
22 |
22 |
22 |
|
|
|
|
|
|
22 |
22 |
22 |
24 |
24 |
24 |
|
|
|
|
|
|
24 |
24 |
24 |
24 |
24 |
26 |
|
|
|
|
|
|
26 |
26 |
26 |
26 |
26 |
26 |
|
|
|
|
|
|
30
