III Проверка выполнения условий адекватности модели

Существует 4 обязательных свойства, которым должны отвечать «Остатки», чтобы найденное уравнение регрессии было адекватным:

• Случайность колебаний уровней остаточной последовательности;

• Соответствие распределения случайной компоненты нормальному закону распределения;

• Равенство нулю математического ожидания случайной компоненты;

• Независимость значений уровней случа йной компоненты.

Рассмотрим способы проверки этих свойств:

1)Для исследования случайности отклонений от уравнения регрессии находят разности ɛ_i= y_i - . В данной задаче используется критерий серий, основанный на медиане выборки. Выборка признается случайной, если для 5% уровня значимости выполняются следующие неравенства :

К_max < [3,3lg(n+1)] ; ν > [1/2 (n+1-1,96√n-1)],

Где К_max- общая протяженность самой длинной серии, а ν- общее число серий. В работе вычислены результаты, согласно которым К_max=2 < 4,

а ν= 12> 6. Отсюда следует, что данная модель отвечает первому свойству.

2)Проверка второго свойства производится с помощью нахождения показателей асимметрии γ₁ и эксцесса γ_2. В качестве оценки асимметрии используются формулы : ,,,, где γ₁ и γ₂ – выборочные характеристики асимметрии, а σ_y1 и σ_y2 их среднеквадратические ошибки.

Если одновременно выполняются условия || < 1,5 σ_y1 , и

<1,5 σ_y1 то гипотеза о нормальном распределении принимается. В данной работе

В данной работе = -0,72 ,=1,16, σ_y1 =0,47, σ_y2 =0,76. Гипотеза не выполняется, соответственно данная модель не отвечает второму свойству.

3)Проверка адекватности осуществляется на основе t- критерия Стьюдента по формуле ,

где 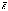- среднее арифметическое значение, а S_ɛ- стандартное среднеквадратическое отклонение для этой последовательности. Т.к расчетное t = 2,059Е-14 меньше табличного ,то гипотеза о равенстве нулю математического ожидания случайной последовательности принимается.

4)Проверка независимости значений уровней случа йной компоненты производится на основе d – критерия Дарбина – Уотсона по формуле:

Далее сравниваем полученное значение с критическими верхним d₂ и нижним d₁ . В работе получено значение d = 2, 25. Это значение больше верхнего табличного d₂ , а значит гипотеза о независимости уровней остаточной последовательности принимается.

Іv Определение точности модели

Точность модели характеризуется величиной отклонения выхода модели от реального значения моделируемой переменной. Для показателя , представленного рядом значений, точность определяется как разность между значениями фактического уровня ряда и его оценкой, полученной расчетным путем с использованием моделей. При этом в качестве статистических показателей точности применяют следующие :

1)Среднее квадратическое отклонение

Где i = 1…n;

-фактическое значение ряда

-теоретическое значение ряда;

n- количество наблюдений;

p- количество независимых параметров.

Значение среднего квадратического отклонения в работе = 6,23

2)Средняя относительная ошибка аппроксимации

Результат, полученный в работе =90,74

3)Коэффициент сходимости

Результат, полученный в работе = 5,38

4)Коэффициент детерминации

Результат, полученный в работе = -4,38

Выводы

Множественный R, характеризующий тесноту связи между результирующим показателем и независимыми переменными, равен 0,99 (R приближено к 1) показывает, что связь между Y с одной стороны и аргументами х₂ , х₃ с другой стороны является функциональной и линейной;

Значение множественного коэффициента детерминации (R²), равное 0,98 свидетельствует о значительном влиянии включенных в модель факторов на результирующий показатель;

Стандартная ошибка - это допустимое отклонение теоретического результирующего фактора от фактического. В рассматриваемом варианте она равна 16,74;

Уровень значимости F = 1,003T-15 характеризует среднюю вероятность принятия нулевой гипотезы по уравнению в целом; коэффициенты уравнения регрессии: b₁ = 0,66, b₃ = 13,03 - показывают среднее изменение результата с изменением факторов на одну единицу, коэффициент а = 31,75. Формально а - значение при х₁ и х₃ = 0. Если признак фактор Х не имеет и не может иметь нулевого значения, то трактовка свободного члена а не имеет смысла. Параметр а может не иметь экономического содержания. Интерпретировать можно только знак при параметре а.

Р-значение - это вероятность принятия нулевой гипотезы по каждому коэффициенту уравнения регрессии. В данном расчетном случае она составляет 0,07

Нижние 95% и верхние 95% - это уровень доверия, которому соответствует 5%-ный уровень значимости, то есть вероятности ошибки. Значения этих показателей определяют минимальный и максимальный уровень коэффициентов, используемых в уравнении при 5%-ном уровне значимости.

На основании этих характеристик можно сделать вывод, о том, что модель достаточно точна, адекватна и пригодна для прогнозирования.

Корреляционная связь, описанная уравнением:

у = 58,15 + 0,58х₂ + 8,18х₃

с большой долей вероятности точно характеризует взаимосвязь результирующего показателя (производительности труда) с энерговооруженностью и процентом прибыли.