5. Координати вектора у векторному просторі. Розкладання вектора за базисом

Для того, щоб вектори з векторного простору можна було б задавати за допомогою чисел і зводити операції над векторами до операцій над числами, вводиться поняття координат вектора.

Нехай – деякий базис векторного простору. Тоді будь-який векторможна подати у вигляді (1)

де – деякі дійсні числа, причому єдиним чином. В цьому випадку вираз (1) називається розкладом вектораза базисом.

Означення. Коефіцієнти розкладу (1) називаються координатами вектора в даному базисі. Упорядкований набір координат вектора називається його координатним рядком і позначається :

.

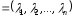Таким чином, базис дає змогу кожен вектор однозначно зобразити рядком чисел – координат цього вектора. Це зображення дозволяє виконувати над векторами лінійні операції за правилами лінійних операцій над матрицями-рядками: якщо ів деякому базисі, то

,

.

Зауваження. Разом із координатними рядками можна розглядати координатні стовпці , отримані транспонуванням-матриці.

Приклад. Довести, що вектори утворюють базис у просторіта знайти координати векторав цьому базисі.

, ,,

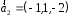Розв’язання. 1) Перевіримо необхідну і достатню умову компланарності векторів :

.

Оскільки , то вектори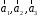некомпланарні, тому вони лінійно незалежні і утворюють базис.

2) Розкладемо вектор за базисом:

або в координатному вигляді:

Вектори рівні, коли їх відповідні координати рівні. Тому одержимо систему :

Розв’язуючи цю систему будь-яким способом, знайдемо , ,.

3) Отже, .

.

Відповідь:

6. Ізоморфізм векторних просторів

Елементами векторних просторів можуть біти об’єкти різної природи: напрямлені відрізки, впорядковані набори чисел, матриці, многочлени, функції, тощо. При вивченні векторних просторів інтерес являють не самі вектори, а операції над ними і властивості цих операцій. Може статися так, що, хоча вектори яких-небудь двох лінійних просторів за своєю природою абсолютно різні, з точки зору властивостей операцій над векторами ці простори не розрізняються.

Нехай і– векторні простори над одним й тим самим полем.

Означення. Простори і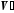називаютьсяізоморфними, якщо між ними існує ізоморфізм – взаємно однозначна відповідність, яка задовольняє умовам:

1. якщо векторам івекторного просторувідповідають вектори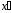івекторного простору, то векторувідповідає вектор:

.

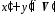2. якщо вектору відповідає вектор, то для будь-якоговекторувідповідає вектор:

.

Приклади ізоморфних просторів.

1) Дійсний векторний простір ізоморфний дійсному 3-вимірному арифметичному простору, оскільки кожному векторуможна поставити у взаємно однозначну відповідність рядок його координат в деякому фіксованому базисі. При такій відповідності будуть виконуватися співвідношення:

,

.

2) Дійсний векторний простір квадратних матриць другого порядку над полеміз звичайними операціями додавання матриць і множення матриць на елементи з поляізоморфний дійсному 4-вимірному арифметичному простору, оскільки кожній матриціможна поставити у взаємно однозначну відповідність вектор-рядокі при цьому будуть виконуватися співвідношення:

.

3) Векторний простір всіх многочленів від змінноїстепеняз дійсними коефіцієнтами відносно операцій додавання многочленів і множення многочленів на число ізоморфний дійсному 3-вимірному арифметичному просторуоскільки кожному многочленуможна поставити у взаємно однозначну відповідність вектор-рядокі при цьому будуть виконуватися співвідношення:

,

.

З означення ізоморфізму векторних просторів і безпосередньо випливають наступні

Властивості ізоморфізму векторних просторів:

При ізоморфізмі векторних просторів і

1. .

2. .

3. Якщо векторам відповідають вектори, то лінійній комбінаціїз довільними коефіцієнтами відповідає лінійна комбінаціяз тими самими коефіцієнтами.

4. Кожному базису в 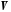відповідає базис в.

Теорема (про ізоморфні векторні простори). Векторний простір , ізоморфний скінченновимірному векторному простору, є скінченновимірним і має ту ж саму розмірність , що й. Будь-які два скінченновимірних векторних простораіоднієї розмірності ізоморфні.

Наслідок. Всі векторні простори над одним й тим самим полем однакової розмірності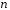ізоморфні-вимірному арифметичному просторунад полем.