высшая математика

Приведенные определения связаны между собой следующей теоремой.

Теорема 6.

Чтобы БМФ f и g были эквивалентны в окрестности точки а, необходимо и достаточно, чтобы

f (x) = g (x) + o (g (x)) при x → a.

Геометрическая интерпретация соотношений (2) приведена на рис. 4 .

162

Здесь мы воспользовались также непрерывностью функции ln x на (0, +∞ ).

! Задания для самостоятельной работы

163

Лекция 27

Понятие производной. Правила дифференцирования

Вводится понятие производной. Исследуется ее геометрический и физический смысл. Приводятся правила дифференцирования суммы, разности, произведения и частного.

10. Пусть функция у = f (х) определена и непрерывна в окрестности точки х = а. Если независимому переменному х придать приращение ∆ x в этой точке, то функция получит соответствующее прира-

Если же мы хотим получить представление, как быстро изменяется значение функции при изменении независимого переменного в окрестности точки х = a, то должны сопоставить или сравнить какимто образом приращение аргумента ∆ x и приращение функции ∆ y . С целью более глубокого изучения функции, исследования скорости изменения ее значений вводится понятие производной – одно из важнейших понятий математики.

Производной функции y = f (x) в точке х = а называется предел отношения приращения функции в этой точке к приращению аргумента

164

Учитывая, что существуют вышеуказанные односторонние пределы, в этом случае говорят, что у рассматриваемой функции существуют односторонние производные в точке х = 1 (правая и левая, соответственно).

Выясним связь между существованием производной в точке и непрерывностью функции.

Теорема 1.

Это означает, что функция y = f (x) непрерывна в точке х.

165

Обратное утверждение неверно. Функция может быть непрерывной в точке, но не иметь в ней производной. Это видно на примере 2. Функция y =|x –1| в точке х = 1 непрерывна, но не имеет в ней производной.

20. Геометрический смысл производной. Пусть функ-

ция y = f (x) определена на интервале (а, b). Предположим, что кривая АВ является графиком этой функции (рис. 1). Пусть M (x0; f (x0)) – какаялибо точка графика. Придадим аргументу приращение ∆ x в точке x0. Соответствующую точку на графике обозначим через

P(x0 + ∆ x; f (x0 + ∆ x)) .

Через точки М и Р проведем прямую и назовем ее секущей. Если точку Р устремить по кривой АВ к точке М, то положение секущей будет, вообще говоря, изменяться, и ее предельное положение (если оно существует) называется касательной к кривой АВ в точке М. Обозначим через α угол между касательной МТ и осью Ох (или, что то же самое, между касательной МТ и прямой MN, рис. 1), а через ϕ – угол между секущей МР и осью Ох, т.е. α – угол наклона касательной МТ к оси Ох, а ϕ –

Итак, геометрический смысл производной функции состоит в том,

Рис. 1

166

что производная функции y = f (x) в точке x = x0 есть тангенс угла наклона касательной к ее графику в точке (x0; f (x0)). Другими слова-

ми, f ′(x0 ) есть угловой коэффициент касательной к графику функ-

ции в точке M (x0; y0). Поэтому уравнение касательной имеет вид:

Прямая, проходящая через точку (x0; f (x0)) и перпендикулярная касательной, называется нормалью к графику в этой точке. Учитывая условие перпендикулярности двух прямых, можем записать уравнение нормали:

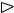Пример 3. Найти уравнение касательной и нормали к графику функции y = 2u + 3u–2 в точке (1; 5).

Решение. Полагаем u0 = 1. Очевидно, у (1) = 5.

Найдем y′(1) : y′= 2 − 6u− 3 , y′(1) = 2 − 6 = − 4 . Теперь воспользуемся соотношением (2) и запишем уравнение касательной в точке (1; 5):

y – 5 = (–4) (u – 1), y – 5 = –4u + 4, y = –4u + 9.

Уравнение нормали будет иметь следующий вид:

y − 5 = 14 (u − 1), y = 14 u + 4,8 .

30. Физический смысл производной. Пусть некоторая материальная точка М движется прямолинейно и задан закон ее движения s = s (t), т.е. известно расстояние s (t) от точки М до некоторой на-

чальной точки отсчета в каждый момент времени t. В момент време-

ни t0 точка пройдет расстояние s (t0) , а в момент времени t0 + ∆ t – расстояние s (t0 + ∆ t) . За промежуток времени ∆ t точка М пройдет расстояние ∆ s = s(t0 + ∆ t) − s( t0) .

Отношение ∆∆ st можно рассматривать как среднюю скорость дви-

жения на промежутке времени [t0 ; t0 + ∆ t ]. Чем меньше промежуток вре-

167

мени ∆ t , тем точнее соответствующая средняя скорость будет характеризовать движение точки в момент времени t0. Поэтому предел средней скорости движения при ∆ t → 0 называют скоростью движения

(или мгновенной скоростью движения) точки М в момент времени t0 и обозначают v (t0), т.е.

v(t0 ) = ∆limt → 0 s(t0 + ∆∆tt) − s(t0) .

Но выражение справа есть s′(t0) . Таким образом, v(t0) = s′(t0) , т.е. скорость движения в момент времени t0 есть производная от пройденного расстояния по времени.

Понятие скорости, заимствованное из механики, удобно использовать и при изучении произвольной функции. Какую бы зависимость ни

отражала бы функция y = f (x), отношение ∆∆ xy есть средняя скорость из-

менения зависимой переменной у относительно аргумента х, a y′(x) есть

скорость изменения у в точке х.

Проиллюстрируем справедливость данного утверждения следующим образом.

40. Экономический смысл производной.

Пусть u = u (t) выражает количество произведенной продукции и за время t на некотором предприятии. Необходимо найти производи-

168

! Задания для самостоятельной работы

1. Пользуясь определением, найти производные следующих функций в заданной точке x0:

а) у = 5х2 + 2х + 1, x0 = 1; б) y = x 3 – 3x + 2, x0 = –1.

2. Написать уравнение касательной и нормали к графику функции y = f (x) в точке, абсцисса которой равна x0. Найти угол наклона касательной к оси Ох:

а) у = 5х2 + 2х + 1, x0 = 1; б) y = x 3 – 3x + 2, x0 = –1.

3. Точка движется прямолинейно по закону s = s (t). Найти скорость в момент времени t0:

а) s = 2t3 + 2t2 + 1, t0 = 0; б) s = 1 + t + t3, t0 = 1.

4. Объем продукции u, произведенной бригадой рабочих, может быть описан уравнением

u = 125 t 2 + 100t + 50 (ед.), 1 ≤ t ≤ 8 ,

где t – рабочее время в часах. Вычислить производительность труда в

170