
высшая математика
.pdf
Значит, n N : 0 < xn < |
1. Следовательно, последовательность |
{xn } является возрастающей, |
ограниченной и имеет предел. |
! Задания для самостоятельной работы
1. Доказать сходимость и найти предел последовательности {xn },
где x1 = |
a, |
x2 a + |
a, $, |
|
xn = |
a + |
a + $+ a (всего n корней),..., a > 0. |
2. |
Найти предел последовательности {xn }, которая определяет- |
||
ся рекурентным соотношением: х1 |
– произвольное число, х1 (0; 1) ; |
||
n N : xn+1 = xn (2 – хn). |
|
{xn },если |
|
3. |
Найти предел последовательности |
||
|
x1 = a, x2 = b, a < b, xn = |
xn− 1 + xn− 2 |
, n = 3, 4, $ . |
|
2 |
||
|
|
|
|
4. |
Доказать, что неограниченная монотонная последовательность |
||
является бесконечно большой. |
|
|
|
131

 Лекция 23
Лекция 23
Понятие функции
Приводятся определение функции и способы задания функций. Вводятся понятия обратной и сложной функций. Рассматриваются классификация функций и построение графиков функций.
10. При изучении явлений природы, физических, экономических и др. процессов часто встречаются с совокупностью переменных величин, которые связаны между собой так, что значения одних величин полностью определяют значения других. Например, площадь круга S однозначно определяется значением его радиуса с помощью формулы
S = π r2.
Пусть Х и У – два произвольных множества действительных чисел Х R , У R. Если каждому элементу х из множества Х по некоторому правилу f поставлен в соответствие определенный элемент у из множества У, то говорят, что задана функция f. Для обозначенияf функции f используются такие обозначения : у = f (х), X → Y , f : x → у.
Переменная х называется независимой переменной, или аргументом функции, переменная у – зависимой переменной, или значением функции. Множество Х называют областью определения, или облас-
тью существования функции f. Множество всех значений у, у У
функции y = f (x), х |
Х называется множеством значений функции. |
Например, функция |
y = 1− x2 определена на отрезке [–1; 1], т.е. |
областью определения является множество Х = [–1; 1]. Множеством зна-
чений функции |
в данном случае является отрезок [0; 1], Y = [0; 1]. |
|||||||||||||
Функция, |
все значения которой равны между собой, называется |
|||||||||||||
постоянной. Постоянную функцию часто обозначают буквой C. |
||||||||||||||
Функция f, определенная на множестве Х, называется ограничен- |
||||||||||||||
ной, если M > 0 такое, что x X : f (x) | ≤ |
M. |
Например, |
функция |
|||||||||||
y = cosx является ограниченной на R, так как |
|
x |
|
R : |cos x| ≤ |
1, а функ- |
|||||||||
ция у = tg х не является ограниченной на интервале − |
|
π |
; |
π |
, так как не |
|||||||||
2 |
|
|||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|||||
|
|
|
|
π |
|
|
π |
|
|
|
|
|
||
существует числа M > 0 такого, чтобы х |
− |
|
|
; |
|
|
: |tg x| ≤ |
M. |
||||||
2 |
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||
132
Графиком функции называется множество всех точек плоскости с координатами (x; f (x) ), т.е. координаты x и y точек г р а ф и к а
связаны соотношением у = f (x). Например, графиком функции у = х2 является парабола. Естественно, что графиком функции не обязательно является «сплошная» кривая. В частности, графиком функции у = n! будет бесконечное множество изолированных точек (нарисуйте!).
20. Способы задания функции. Чтобы задать функцию,
требуется указать правило: как по каждому значению аргумента х находить соответствующее значение функции у = f (x). Существуют три основных способа задания функции: аналитический, табличный и графический.
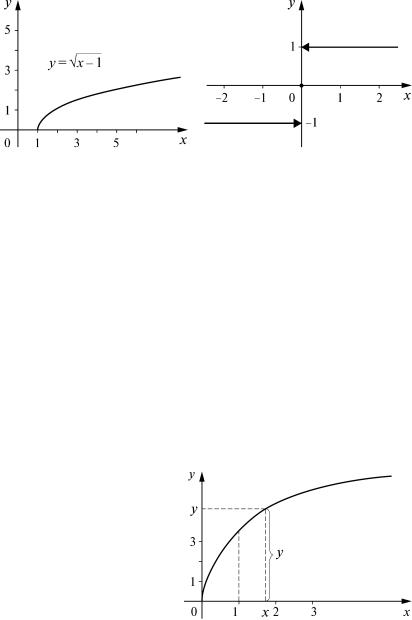
1) А н а л и т и ч е с к и й с п о с о б . Если зависимость между переменными выражена с помощью формул, то говорят, что функция задана аналитически. Формула, задающая функцию, указывает совокупность действий, которые нужно в определенном порядке произвести, чтобы получить соответствующее значение функции. Рассмотрим, напри-
мер, функцию y = |
x − 1 . Функция, заданная этой формулой, определена |
|
на |
промежутке |
[1; + ∞ ). Чтобы вычислить значение функции |
|
х [1; + ∞ ), необходимо от значения аргумента х вычесть 1 и извлечь |
|
из полученного числа квадратный корень. Множеством значений является промежуток [0; + ∞ ).
Графиком функции является множество всех точек плоскости с
координатами |
(x ; x − 1), переменная х пробегает здесь промежуток |
[1, + ∞ ) (рис. |
1а). |
|
1, |
если x |
(0; + |
∞ ), |
Пусть |
|
если x = |
0, |
|
0, |
|
|||
|
|
если x |
(− ∞ |
; 0). |
|
− 1, |
Данная функция выражена при помощи нескольких формул. Областью определения является вся числовая прямая, множество значений состоит из трех элементов: –1, 0, 1. График см. на рис. 1б. Рассматриваемую функцию обозначают у = sign x.
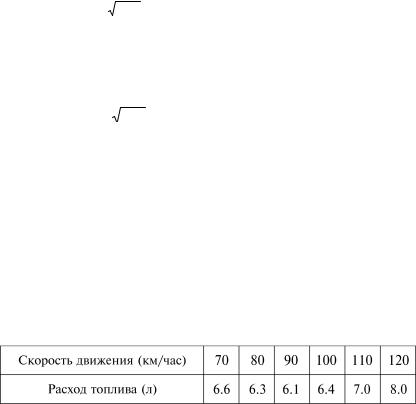
2) Т а б л и ч н ы й с п о с о б . Предположим, что нас интересует зависимость расхода топлива от скорости движения легкового автомобиля определенной марки. В инструкции к автомобилю имеется следующая таблица:
133
а) |
б) |
|
Рис. 1 |
Из таблицы видно, что расход топлива изменяется в зависимости от скорости движения автомобиля и, если каждому значению скорости, записанному в первой строке таблицы, поставить в соответствие число литров топлива, стоящих во второй строке и в этом столбце, то получим функцию, заданную таблично. Областью определения этой функции является множество из 6 чисел, стоящих в первой строке. Множеством значений является также совокупность из 6 чисел второй строки.
С помощью таблицы часто задают функции, значения которых вычислить сложно. Например, широко известны таблицы тригонометрических функций, показательной и логарифмической функций и т.д.
Заметим, что имеются способы перехода от функций, заданных таблично, к функциям, которые заданы аналитически. Безуслов-
но, это можно сделать, как правило, лишь приближенно.
3) Г р а ф и ч е с к и й с п о с о б . В данном случае предполагается, что задан график функции у = f (х) ( см., например, рис. 2).
Здесь, чтобы для неко- |
|
|
торого значения аргумента х |
|
|
найти соответствующее значе- |
|
|
ние функции, нужно построить |
|
|
на оси Ох точку х, затем вос- |
|
|
становить в этой точке пер- |
|
|
пендикуляр к оси Ох, найти |
|
|
точку пересечения этого пер- |
|
|
пендикуляра с графиком и най- |
|
|
ти длину этого перпен- |
|
|
дикуляра. Значение функции |
|
|
будет равно этому числу с со- |
Рис. 2 |
|
ответствующим знаком. |
||
|
134

Примерами графического изображения могут быть записи самопишущих приборов ( барографы, осциллографы и т.д.).
30. Понятие обратной и сложной функции. Пусть на множестве Х задана функция f. Обозначим через Y множество значе-
ний функции f на множестве Х, т.е. Y = {f (x) x X }. Возьмем произ-
вольный элемент у Y и поставим ему в соответствие одно или несколько значений переменной х Х таких, что f (х) = у. Таким образом мы определили на множестве Y функцию, которая называется обратной к функции у =f (х) и обозначается х = f –1 (у) или f –1, f –1: у → х. Если каждому у Y соответствует только одно значение х Х такое, что f (х) = у, то говорят, что обратная функция однозначна, если соответствует несколько значений х Х, удовлетворяющих условию f (х) = у, то это соответствие не есть, вообще говоря, функция в обычном смысле. В этом случае говорят, что обратная функция является многозначной. Так, для функции у = 2х существует обратная функция (одно-
значная!) x = 2y , а для функции у = х2 обратная функция является
двузначной: x = ± y .
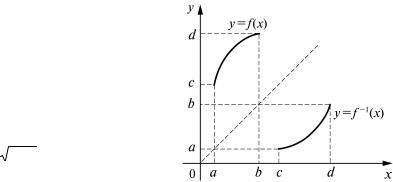
Предположим, что для функции у = f (х), заданной на отрезке [a; b], существует однозначная обратная функция х = f –1 (y). Пусть множеством значений функции f является отрезок [c; d]. Тогда этот отрезок является областью определения обратной функции f- –1, а отрезок [a; b] – множеством ее значений. Графики функции у = f (х) и ее обратной х = f- –1 (y) будут совпадать, если в первом случае аргумент откладывать вдоль оси Ох, а во втором – вдоль оси Оу (рис. 3).
Если же условиться и в случае функции f, и в случае обратной функции f –1 независимую переменную обозначать через х, а зависимую – через у, то для того, чтобы получить график функции у = f –1 (х) из графика у = f (х), нужно первый график зеркально отобразить относительно биссектрисы I и III четвертей координатной плоскости (рис. 4).
Пусть на некотором мно-
жестве Х задана функция f : х → у с множеством зна-
чений Y, а на множестве Y в
135
свою очередь задана функция g : y → z. Тогда на множестве Х можно определить функцию
ϕ : х → z такую, что z = g (f (x) ). Функция z = ϕ (x)
или z = g (f (x) ) называется сложной функцией, или суперпозицией двух функций y = f (x) и z = g (y). Например, функция
z = cos x |
является сложной |
|
функцией, |
суперпозицией |
|
тригонометрической функции |
Рис. 4 |
|
y = cos x и степенной z = y1/2. |
||
Функция y = e2x+1 также явля-
ется сложной функцией, суперпозицией линейной функции t = 2x + 1 и показательной у = еt.
Функция, заданная уравнением, не разрешенным относительно зависимой переменной, называется неявной. Например, уравнение х2 + у2 = 1 определяет у как неявную функцию от х.
40. Классификация функций производится в зависимости от вида действий, которые необходимо выполнить над значением аргумента, чтобы получить значение функции.
1) Если над значением аргумента и некоторыми постоянными производится конечное число действий сложения, вычитания, умножения и возведения в целую положительную степень , то соответствующая функция называется целой рациональной, или алгебраическим многочленом. Такая функция может быть записана в виде
P(x) = a |
0 |
xn + |
a xn− 1 |
+ |
a |
2 |
xn− 1 |
+ |
$+ |
a |
n− 1 |
x + |
a |
n |
, |
|
|
1 |
|
|
|
|
|
|
|
|
|
где n ≥ 0 – целое число, a0, a1,..., an – любые числа, коэффициенты многочлена. Если a0 ≠ 0, то P (x) называют многочленом степени n.
2) Функция R (x), являющаяся отношением двух многочленов (целых рациональных функций), называется дробной рациональной фун-
кцией, т.е. R(x) = |
a0 xn + |
a1xn− 1 |
+ |
$+ |
an− 1x + |
an |
. |
|
b xm + |
b xm− 1 |
+ |
$+ |
|
|
|||
|
b |
x + |
b |
|||||
|
0 |
1 |
|
|
m− 1 |
|
m |
|
Множество целых и дробных рациональных функций образует класс рациональных функций.
136

3) Если над аргументом x производятся не только перечисленные выше операции, но и операция извлечения корня, и полученный результат не является рациональной функцией, то говорят, что задана иррацио-
нальная функция. Например, f (x) = |
2x + 1 |
, f (x) = |
x 2 + x + 1+ 3 x |
являются иррациональными функциями. |
x − 3 |
|
|
|
|
|
4) Любая функция, не являющаяся рациональной или иррациональной, называется трансцендентной. Простейшими трансцендентными функциями являются:
а) тригонометрические функции: sin x, cos x, tg x, ctg x, sec x, cosec x;
б) обратные тригонометрические функции: arcsin x, arccos x и т.д.; в) показательная функция ах, a > 0, a ≠ 1;
г) логарифмическая функция loga x, a > 0, a ≠ 1.
Функции рациональные, иррациональные, трансцендентные и конечное число их суперпозиций составляют класс элементарных функций. Это те функции, которые и будут изучаться.
50. Построение графиков функций. В настоящем пункте,
предполагая, что графики простейших рациональных и трансцендентных функций известны, рассмотрим построение графиков функций с помощью линейных преобразований.
Пусть задана функция у = f (х) и ее график известен (рис. 5).
1) |
График функции у = f (х) + с |
получается из графика функции |
у = f (х) |
с помощью параллельного переноса последнего вдоль оси Оу |
|
на величину, равную с (рис. 6). |
|
|
2) |
График функции у = f (х – а) |
получается из графика функции |
у = f (х) |
с помощью сдвига последнего вдоль оси Ох на величину, рав- |
|
ную а (рис. 7).
3) График функции у = k f (х), k > 0 получается из графика функции у = f (х) растяжением в k раз вдоль оси Оу ( при k < 1– сжатием). Если k < 0, то график функции у = k f (х) получается из графика функции у = – k f (х) «зеркальным» отображением относительно оси Ох (рис. 8).
4) График функции у = f (k х), k > 0 получается из графика функции у = f (х) растяжением или сжатием (при k < 1) вдоль оси Ох. При k < 0 нужно «зеркально» отобразить график функции у = f (–k х) относительно оси Оу.
137
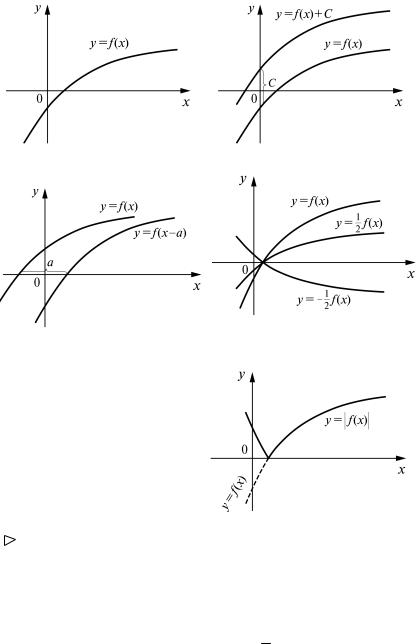
Рис. 5
Рис. 7
Остановимся еще на одном часто встречающемся преобразовании графиков функций. Чтобы получить график функции у = |f (x)|, нужно участки графика функции у = f (х), лежащие выше оси Ох, оставить без изменений, а участки графика, лежащие ниже оси Ох, «зеркально» отобразить относительно этой оси (рис. 9).
Пример 1. Найти f (2),
Рис. 6
Рис. 8
Рис. 9
|
1 |
|
|
2 |
|
|
f |
|
, f (– х), если f (х) = 1 |
+ х + х |
. |
||
x |
||||||
|
|
|
|
|
||
|
|
Решение. |
Очевидно, |
f (2) = 1 + 2 + 22 = 7. Если вместо незави- |
||
симого переменного подставить выражение x1 , то получим:
138
|
|
1 |
1 |
|
|
1 2 |
|
|
1+ |
x + x2 |
|
||
|
f |
|
= 1+ |
x |
+ |
|
|
= |
|
|
|
. |
|
|
|
|
|
x2 |
|||||||||
|
|
x |
|
|
x |
|
|
|
|
|
|||
Аналогично, f (–х) = 1 + (–х) + (–х)2 = 1 – х + х2. |
|||||||||||||
Пример |
2. Определить |
область |
существования функции |
||||||||||
y = x2 − 3x + |
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
Решение. В этом случае подкоренное выражение должно быть |
|||||||||||||
неотрицательно, х2 – 3х + 2 ≥ |
0 . |
|
|
|
|
|
|
|
|||||
Решая это неравенство, получим, что областью определения яв- |
|||||||||||||
ляется множество D = (–∞ ; 1] [2; + ∞ |
). |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
||
Пример 3. Для функции |
|
y |
= ln |
|
|
|
|
найти обратную. |
|||||
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Очевидно, данная функция определена на промежутке (0, ∞ ). Множеством ее значений является R. С помощью потенцирова-
ния находим |
ey |
= |
|
x |
. Значит, х = 2еу |
является обратной функцией к |
||
|
2 |
|||||||
|
|
|
|
|
|
|||
функции y = |
x |
|
|
у |
|
|||
ln |
|
|
. Функция х = 2е |
|
определена на R, множеством ее |
|||
2 |
|
|||||||
|
|
|
|
|
|
|
||
значений является промежуток (0, + ∞ ).
Пример 4. Представить сложную функцию y = arcsin3x в виде суперпозиции соответствующих функций.
Решение. Данная сложная функция является суперпозицией степенной функции u = 3x и обратной тригонометрической функции y = arcsin u.
Пример 5. Построить график функции
у = |1 + (x – 1)3|. |
|
Решение. В качестве исходного возьмем |
|
график функции у= х3 (рис. 10а). С помощью сдви- |
|
га на величину а= 1 вправо вдоль оси Ох получим |
|
график функции у=(х– 1)3 (рис. 10б). Если сделать |
|
перенос полученного графика вдоль оси Оу на одну |
|
единицу вверх, то получим график функции |
|
у= 1+(х– 1)3 (рис. 10в). Наконец, «зеркально» ото- |
|
бражая ту часть графика, которая расположена ниже |
|
оси Оx, получим график функции у= |1+ (x –1)3| |
Рис. 10а |
(рис. 10г). |
139
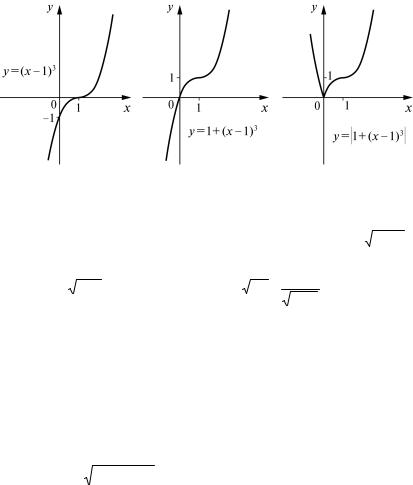
Рис. 10б |
Рис. 10в |
|
|
Рис. 10г |
|||||
! Задания для самостоятельной работы |
f (x) = 1+ x2 . |
||||||||
1. |
Найти f (0), f (–3 / 4), |
f (–x), f (1 / x), 1 / f (x), если |
|||||||
2. |
Определить область существования функций: |
||||||||
а) |
y = |
x + 1 , б) y = lg |
2 + x |
, в) y = |
− x + |
1 |
, |
||
|
3 2 + x |
||||||||
|
|
|
2x |
|
2 − x |
|
|
||
г) |
y = |
arccos |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1+ x |
|
|
|
|
|
||
3. |
Для функции у = f (х) найти обратную, |
если: |
|
||||||
а) |
f(х) = 3х + 2; б) f (x) = arctg 3x; в) |
f (x) = 2e3x. |
|
||||||
4. |
Представить сложную функцию у = f (х) в виде суперпозиций |
||||||||
соответствующих функций, |
если: |
|
|
|
|||||
а) f (x) = ( 2x − 3) 99 ; б) f (x) = lg
г) f (x) = sin3(5x + 3) ; д) f (x)
|
x |
|
|
; в) f (x) = arcsin 3 |
− x2 |
; |
|||
tg |
|
|
|
|
|
||||
3 |
|
||||||||
|
|
|
|
|
|
|
|
||
= ln |
2 1− |
x |
|
|
|||||
|
|
|
. |
|
|
||||
|
|
1+ |
x |
|
|
||||
5. Построить графики следующих функций:
а) у = х3 – 2; б) у = 1/ (х – 1); в) y = lg (x + 2);
|
x |
|
|
|
|
π |
|
|
1 |
|
1 |
|
г) y = 1 – 0,5 |
|
; |
д) |
y = |
2cos x − |
|
; е) |
y = |
|
+ |
|
arctg x ; |
|
|
|
|
|
|
4 |
|
|
2 |
|
π |
|
ж) y = |x3 – 3x + 2|; з) y = |1 + ln x|.
6. Построить графики в полярной системе координат: а ) r = 1 (окружность) ; б) r = 1 / sin ϕ (прямая);
в) r = 2cos ϕ (окружность); г ) |
r = sec2 |
ϕ |
(парабола). |
|
|||
|
2 |
|
|
140
