
- •1.Дифференциальные уравнения(д.У.) первого порядка. Общее и частное решение д.У. Задача Коши.
- •2. Теорема существования и единственности решения задачи Коши для дифференциального уравнения (д.У.) первого порядка.
- •2.Однородные ду
- •5.Ду высшихпорядков: постановка задачи Коши, теорема сущ-ния и един-ти решения задачи Коши.
- •8.Линейная зависимость,независимость ф-ий. Определитель вронского.
- •9.Линейные однородные уравнения высших порядков с постоянными коэф-тами. Характеристическое ур-е Зависимость общего решения от корней характер-го ук-я.
- •12Линейные однородные системы ду высших порядков с постоянными коэффициентами
- •13.Линейные неоднородные системы ду высших порядков с постоянными коэффициентами. Системы со специальной правой частью.
- •15 Устойчивость по Ляпунову
- •16 Устойчивость по первому приближению
- •19.Предел и непрерывность функций комплексной переменной.
- •22.Элеменарные функции комплексной переменной.
- •25.Теорема Коши и интегральная формула Коши.
- •26. Cтепенные ряды в комплексной области. Теорема Абеля, радиус сходимости
- •27. Ряд Тейлора. Разложение некоторых элементарных функций в ряд Тейлора
- •28. Нули аналитических функций. И их классификация.
- •29. Ряд Лорана. Изолированные особые точки и их классификация.
- •32. Вычет аналитических функций.
- •35.Классификац.Ур. Матфизики.
- •42. Оригинал и изображение. Св-ва преобразования Лапласа: линейность, подобие.
- •44. Формулы обращения преобразования Лапласа.
- •45. Применение преобразования Лапласа: теоремы обращения.
- •46. Применение преобразования Лапласа. Решение линейных д. У. С помощью преобразований Лапласа.
- •47. Применение преобразования Лапласа к решению физических задач.
- •48. Решение ур-ий с частными производными с помощью преобразования Лапласа.
26. Cтепенные ряды в комплексной области. Теорема Абеля, радиус сходимости
 (1),
где
(1),
где
 и а - действительные числа, наз-ся
степенным рядом с центром х=а. Заменой=х-а
такой ряд приводится к виду (вместо
пишем х):
и а - действительные числа, наз-ся
степенным рядом с центром х=а. Заменой=х-а
такой ряд приводится к виду (вместо
пишем х):
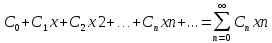 (2)
поэтому можно ограничится изучением
ряда (2). Ряд (2) всегда сходится к точке
х=0: S(0)=C.
(2)
поэтому можно ограничится изучением
ряда (2). Ряд (2) всегда сходится к точке
х=0: S(0)=C.
Т-ма Абеля
Если
ряд (2) сходится в точке
 ,
то он абсолютно сходится прих<
,
то он абсолютно сходится прих<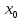 ,
т.е. на ]-
,
т.е. на ]-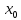 ,
,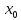 [;
если он расходится в точке
[;
если он расходится в точке
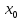 0,
то расходится при х<
0,
то расходится при х<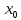 ,
т.е. на ]-,-
,
т.е. на ]-,-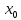 [
и ]
[
и ]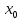 ,+[.
,+[.
Если
сходится
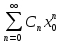 ,
то
,
то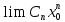 и
сходящаяся последовательность{
и
сходящаяся последовательность{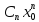 }
ограничена:(n)[
}
ограничена:(n)[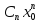 M](n)[|Cn|
M/|
M](n)[|Cn|
M/|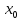 n|.
Если |x|<|
n|.
Если |x|<|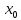 |,
то
|,
то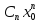 =
=Cn|x|n
M/|
=
=Cn|x|n
M/|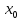 n||x|n=
M(|x|/|
n||x|n=
M(|x|/|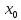 |)n=
=Mqn,
где q=|x|/|
|)n=
=Mqn,
где q=|x|/|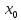 |<1.
Из сходимости геометрического ряда
|<1.
Из сходимости геометрического ряда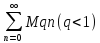 по признаку сравнения следует сход-ть
по признаку сравнения следует сход-ть т.е. абсолютная сход-ть ряда (2) при
рассматриваемомх<
т.е. абсолютная сход-ть ряда (2) при
рассматриваемомх<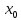 .
Eсли ряд (2) расходится в точке
.
Eсли ряд (2) расходится в точке
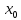 0,
то при х>
0,
то при х>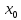
он не может сходится, т.к. по доказанному
он бы сходился в точке
он не может сходится, т.к. по доказанному
он бы сходился в точке
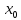
при х>
при х>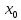
ряд (2) расходится .
ряд (2) расходится .
Т-ма о радиусе сходимости
Для каждого ряда (2)сущ-ет неотрицательное число RŔ такое, что на ]-R,R[ ряд абсолютно сходится, а вне отрезка [-R,R] (т.е. на ]-,-R[ u ]R,+[) расходится.
Если (2) ходится в единственной точке х=0, то полагают R=0 (в точке х= 0 ряд (2) сходится абсолютно). Пусть сущ-ют χ 0, в которых ряд сходится, назовем их точками сход-ти. Мн-во модулей точек сход-ти обозначим Х={ χ }, и пусть R= sup X. Т.к. имеются точки χ 0, т.е. χ >0, то Sup X>0, т.е. R>0. Пусть х<R, тогда х меньшее чем Sup X не может быть верхней границей мн-ва Х и потому найдется χ Х такой, что χ >x. Из сход-ти (2) в точке χ по т-ме Абеля следует абсолютная сход-ть ряда в точке х. Таким образом ряд (2) абсолютно сходится на ]-R,R[. В частности если R=+, то на ]-,+[. Пусть R<+, т.е. R-конечное число, тогда если х>R, то х не может быть точкой сход-ти,
Число R наз-ся радиусом сход-ти степенного ряда (2), ]-R,R[ -интервалом сходимости.
Замечание.
Для степенного ряда (1) интервалом сход-ти явл-ся ]a-R,a+R[.
Если
для
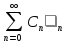 ]-R,R[
-R<
<R, т.е.
-R<x-a<R
a-R< x <a+R
]-R,R[
-R<
<R, т.е.
-R<x-a<R
a-R< x <a+R
27. Ряд Тейлора. Разложение некоторых элементарных функций в ряд Тейлора
Пусть
функция f(x) бесконечно дифференцируема
в некоторой окрестноститочки a.
Формальный ряд: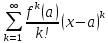 называется рядом Тейлора функции f в
точке a.
называется рядом Тейлора функции f в
точке a.
Это
равенство выолняется(ряд Тэйлора
сходится в окрестнн. Точки a
) если оствток ряда равен:
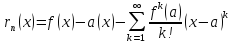 .
Если функция f(x)бесконечно
диференцир. В интервале (a-h,a+h)
и ее производные равеомерно огранич.в
интервале ,т.е существ. Такое пложит.
число C
(не зависещ. от т),что:
.
Если функция f(x)бесконечно
диференцир. В интервале (a-h,a+h)
и ее производные равеомерно огранич.в
интервале ,т.е существ. Такое пложит.
число C
(не зависещ. от т),что: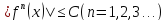 при всехx
из интерв.(a-h,a+h),
то верно равенство во всм интервале
(a-h,a+h).Формула
(1) в частном случае при (a=0)
определяет раздожене в ряд Маклорена:
при всехx
из интерв.(a-h,a+h),
то верно равенство во всм интервале
(a-h,a+h).Формула
(1) в частном случае при (a=0)
определяет раздожене в ряд Маклорена: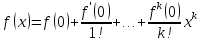
Основные разложения в ряд Тейлора:
1)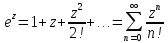
2)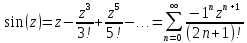
3)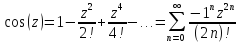
4)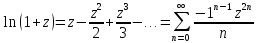
5)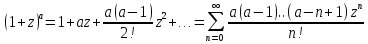
6)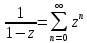
28. Нули аналитических функций. И их классификация.
Пусть
функция f (z) является аналитической в
точке
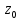 Точка
Точка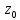 называется нулем функции f (z), если ее
значение в этой точке равно нулю, т.е.
f (
называется нулем функции f (z), если ее
значение в этой точке равно нулю, т.е.
f (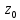 )
= 0.
)
= 0.
В
разложении функции в ряд Тейлора в
окрестности нуля этой функции (т.
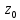 )
отсутствует свободный член:
)
отсутствует свободный член: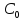 = f(
= f(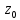 )
= 0.
)
= 0.
Если
при этом в разложении отсутствуют и
слагаемые, содержащие степени разности
(z-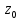 )
до n-ой степени, т.е. разложение имеет
вид:
)
до n-ой степени, т.е. разложение имеет
вид: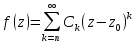 или
f(z)=Cn(z-
или
f(z)=Cn(z-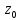 )n+Cn+1(z-
)n+Cn+1(z-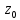 )n+1+…,
Cn≠0 то точка
)n+1+…,
Cn≠0 то точка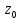 называется нулем порядка n функции f(z).
называется нулем порядка n функции f(z).
Нуль первого порядка (n = 1) называется простым нулем.
Следующие условия являются необходимым и достаточным условиями нуля порядка n функции f (z) в точке z0:
a).
f(n)(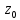 )
≠0, f(k)(
)
≠0, f(k)(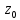 )=0,
k=0,1,… ,(n-1);
)=0,
k=0,1,… ,(n-1);
b).
f(z)=(z-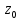 )n*ψ(z),
ψ(
)n*ψ(z),
ψ(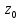 )=Cn
≠0 представление функции в виде
произведения:
)=Cn
≠0 представление функции в виде
произведения:
Порядок
нуля в точке
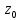 функции, полученной в результате
перемножения аналитических функций
функции, полученной в результате
перемножения аналитических функций
f (z) = f1(z) f2(z) равен сумме порядков нуля (n1 + n2) в этой точке функций сомножителей
(
n1 - порядок нуля в точке
 функции f1(z), n2 - порядок нуля в точке
функции f1(z), n2 - порядок нуля в точке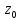 функции f2(z) ).
функции f2(z) ).
