28. Равномерная непрерывность функций

Определение 1. Функция f(x) называется равномерно-непрерывной на множестве X ⊂ R, если для любого ε > 0 найдется δ = δ(ε) > 0, такое, что для любых x₁, x₂ ∈ X, удовлетворяющих условию |x₁−x₂| < δ, выполняется неравенство |f(x₁) − f(x₂)| < ε. Если f(x) равномерно-непрерывна на множестве X, то она непрерывна на множестве X. Чтобы в этом убедиться, достаточно положить x₁ = x, x₂ = x₀. Тогда из определения равномерной непрерывности функции следует определение непрерывной функции в точке x₀. Обратное утверждение не всегда справедливо.

Теорема 8 (Кантора). Функция, непрерывная на отрезке, равномерно непрерывна на этом отрезке. Доказательство. Пусть f : X → R, и f ∈ C([a; b]), где X = [a; b]. Поскольку f(x) непрерывна в любой точке x ∈ X, то по ε > 0 можно найти такую δ-окрестность V_δ(x) точки x, что колебание ω(f, V_δ(x)), где

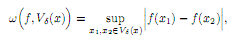
функции f(x) окажется меньше ε. Для каждой точки x ∈ X построим окрестность V_δ(x) обладающую этим свойством. Величина δ при этом может меняться от точки к точке, т.е. δ = δ(x). Интервалы V_δ/2(x), x ∈ X в совокупности образуют покрытие отрезка X = [a; b], из которого по лемме о конечном покрытии можно выделить конечное подпокрытие V_δ/2(x1), . . . , V_δ/2(xn). Пусть δ = min{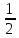δ(x₁), . . . ,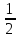δ(x_n)}. Покажем, что для любых точек x’

, x’’∈ X таких, что |x’− x’’| < δ выполнено|f(x’) − f(x’’)| < ε. Действительно, поскольку система интервалов V_δ/2(x₁), . . . , V_δ/2(x_n) покрывает X, то найдется интервал V_δ/2(x_i) этой системы, который содержит точку x’ т.е. |x’− x_i| < 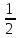δ(x_i). Но в таком случае |x’’− x_i| 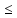|x’− x’’| + |x’− x_i| < δ + 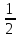δ(x_i) < δ(x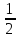_i) +δ(x_i) = δ(x_i). Следовательно x’, x’’∈ V_δ(xi)(x_i) и потому |f(x’) − f(x’’)| ω(f, V_δ(xi)(x_i))< ε.

29.Непр. Элементарн.Ф-ций.

Постоянная функция.Функция f(x) = C, где C = const, ∀x ∈ X непрерывна в любой точке x0, поскольку ==С=f(x₀). Многочлены и рациональные функции.Функция P_n(x) = a₀xⁿ + a₁xⁿ⁻¹+ . . . + aⁿ⁻¹x + aⁿ,где a_i, i = 0, n – действительные числа, называется многочленом от x степени n.Докажем сначала непрерывность функции f(x) = a_kx^k в любой точке x ∈ R. Согласно биному Ньютона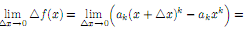

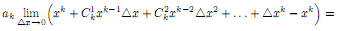
Отсюда заключаем, что функция f(x) = a_kx^k непрерывна в любой точке x ∈ R. Тогда многочлен P_n(x) является непрерывной функцией в любой точке x ∈ R как сумма непрерывных функций вида a_kx^k, k = 0, n. Рациональной называется функция вида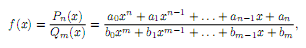

где P_n(x), Q_m(x) – многочлены степеней n и m cоответственно. Рациональная функция во всех точках, в которых Q_m(x) не обращается в нуль, непрерывна как отношение двухнепрерывных функций.Тригонометрические функции:Докажем непрерывность функции f(x) = sin x в любой точке x ∈ R. Имеем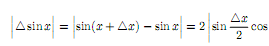

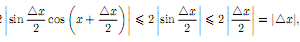
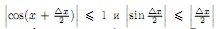
так как Отсюда следует, что если |x| < δ = ε, то и |sin x| < ε, т.е. sin x непрерывная функция в любой точке x∈ R. Аналогично доказывается непрерывность функции cos x в любой точке x ∈ R. Функция tg x = 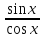непрерывна в точках, где x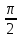+ πn, n∈ Z. Функция ctg x = 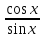непрерывна, если x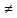πn,n∈ Z.

Степенная функция f(x) = x^a. Непрерывность этой функции при x > 0 вытекает из непрерывности сложной функции и представления x^a = e^{a ln x.} Если же функция x^a имеет смысл и для x < 0 (например, x⁴,³√x), то при a > 0 она будет непрерывной для ∀x ∈ R, а при a < 0 – для всех x ∈ R кроме x 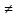0.

30 Дифференцируемость функций. Дифференциал и произв.

Определение 1. Пусть функция y = f(x) определена в некоторой окрестности точки x0 ∈ R и пусть x–произвольная точка этой окрестности. Если отношение 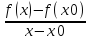имеетgредел при x → x0, то этот предел называется производной функции f(x) в точке x₀, и обозначается f ’(x₀): 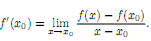Если ввести обозначения x−x₀ = x, f(x₀+x)−f(x₀) = y, то получаем еще одну запись определения производной: Если для

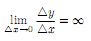
некоторого значения x₀ существуют пределы или то говорят, что при x = x₀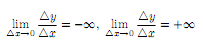

существует бесконечная производная или соответственно бесконечная производная определенного знака, равная −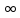или +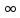.В дальнейшем под выражением «функция имеет производную» будем понимать всегда наличие конечной производной, если не оговорено противное. Определение 2. Если функция f(x) определена в некоторой правосторонней (левосторонней) окрестности точки x₀ и существует конечный или бесконечный (определенного знака) предел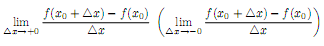

то он называется соответственно конечной или бесконечной правой (левой) производной функции f(x) в точке x₀ и обозначается f ’₊(x₀) (f ’₋(x0)) Правая и левая производные называются односторонними производными. Из теоремы об односторонних пределах следует, что функция f(x), определенная в некоторой окрестности точки x₀, имеет производную f ’(x₀) тогда и только тогда, когда f ’₊(x0) и f ‘₋(x₀) существуют и f’₊(x0) = f’₋(x0). В этом случае f’(x0) = f’₊(x0) = f’₋(x0).Если функция f(x) определена на некотором промежутке и в каждой его точке существует производная (причем под производной в конце этого промежутка, который принадлежит промежутку, понимается соответствующая односторонняя производная), то она также является функцией, определенной на данном промежутке, ее обозначают f’(x). Теорема 1. Для того чтобы функция f(x) была дифференцируемой в некоторой точке x0, необходимо и достаточно,чтобы она имела в этой точке производную, при этом dy = f’(x0) dx.Доказательство. 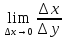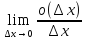Пусть функция f(x) дифференцируема в точке x0, т.е y = A·x+o(x), x → 0.Тогда =A + =A. Поэтому производная f’(x0) существует и равна A. Отсюда dy= f’(x0) dx. Теорема 2. Если функция f(x) дифференцируема в некоторой точке, то она и непрерывна в этой точке. Следствие 1. Если функция в некоторой точке имеет производную, то она и непрерывна в этой точке. Обратим внимание на то, если функция в точке имеет бесконечную производную, то она может быть разрывной в этой точке. Заметим, что утверждение, обратное теореме 2, неверно, т.е. из непрерывности функции f(x) в данной точке не следует ее дифференцируемость.