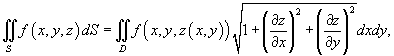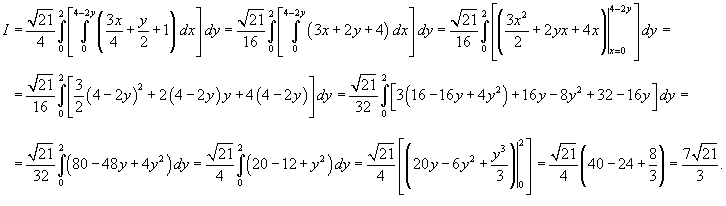- •1.Комплексные числа. Свойства. Формы записи.
- •2.Интегрирование простейших рациональных функций
- •3)Интегрирование рациональных функций методом неопределённых коэффициентов. Метод Остроградского.
- •4.Интегрирование тригонометрических функций
- •Геометрический смысл несобственного интеграла I рода
- •Примеры
- •13. Несобственный интеграл второго рода
- •15. Схема применения определённого интеграла
- •16. Вычисление площади плоских фигур
- •Вопрос 20
- •Вопрос 21 Формула метода трапеций.
- •Графическая иллюстрация метода парабол (Симпсона).
- •Вопрос 23
- •Вопрос 24
- •37 Приложения двойного интэграла 1. Вычисление площадей
- •2. Вычисление объёмов тел
- •3. Центр тяжести плоской фигуры
- •42 Приложения тройного интэграла . Вычисление объёма тела:
- •2. Вычисление массы тела переменной плотности γ (X; y; z):
- •3. Координаты центра тяжести тела с постоянной плотностью:
- •4. Координаты центра тяжести тела с переменной плотностью γ (X; y; z):
42 Приложения тройного интэграла . Вычисление объёма тела:

2. Вычисление массы тела переменной плотности γ (X; y; z):

3. Координаты центра тяжести тела с постоянной плотностью:
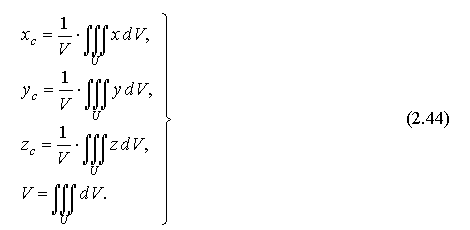
4. Координаты центра тяжести тела с переменной плотностью γ (X; y; z):
БИЛЕТ49
Пусть в области D заданы непрерывные функции P(x,y) и Q(х,y) и M0M - гладкая дуга, лежащая в области D.
Рассмотрим вопрос о независимости интеграла

от формы пути интегрирования. Имеет место следующая теорема.
Теорема 3.3. Пусть функции P, Q, P'y, Q'x определены и непрерывны в односвязной, ограниченной замкнутой области D плоскости Оху. Тогда следующие четыре условия равносильны между собой: 1)
![]()
, где L - замкнутый контур в области D; 2) интеграл
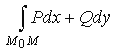
не зависит от формы пути интегрирования, а зависит лишь от положения точек M0 и М; 3) Pdx + Qdy = dU - полный дифференциал некоторой функции U(x,y); 4)
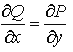
в каждой точке области D.
Идея
доказательства этой теоремы: показывается,
что из условия 1 ![]() условие
2
условие
2![]() условие
3
условие
3![]() условие
4
условие
4![]() условие
1.
условие
1.
Пример 3.7. Вычислить
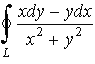
, где контур L не охватывает начало координат.
Решение
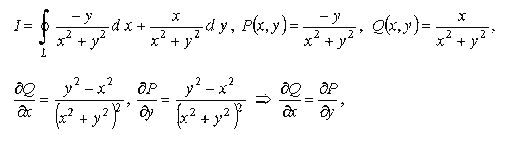
т. е. выполнено условие 4 теоремы. Значит выполнено и условие 1, т. е.
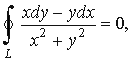
где L – любой контур, не охватывающий начало координат, так как в точке О(0,0) нарушаются условия теоремы, и её выводы в этом случае было бы нельзя применить.
БИЛЕТ50.
С помощью криволинейных интегралов вычисляются
Масса кривой;
Центр масс и моменты инерции кривой;
Работа при перемещении тела в силовом поле;
Магнитное поле вокруг проводника с током (Закон Ампера);
Электромагнитная индукция в замкнутом контуре при изменении магнитного потока (Закон Фарадея).
Рассмотрим эти приложения более подробно с примерами.
Масса кривой
Предположим, что кусок проволоки описывается некоторой пространственной кривой C. Пусть масса распределена вдоль этой кривой с плотностью ρ (x,y,z). Тогда общая масса кривой выражается через криволинейный интеграл первого рода
![]()
Если кривая C задана
в параметрическом виде с помощью
векторной функции ![]() ,
то ее масса описывается формулой
,
то ее масса описывается формулой
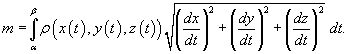
В случае плоской кривой, заданной в плоскости Oxy, масса определяется как
![]()
или в параметрической форме
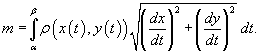
Центр масс и моменты инерции кривой
Пусть снова кусок проволоки описывается некоторой кривой C, а распределение массы вдоль кривой задано непрерывной функцией плотности ρ (x,y,z). Тогда координаты центра масс кривой определяются формулами
![]()
где
![]()
− так называемые моменты первого порядка. Моменты инерции относительно осей Ox, Oy и Oz определяются формулами
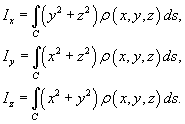
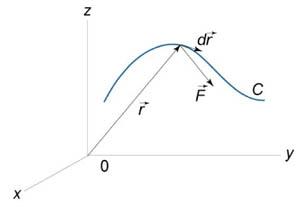
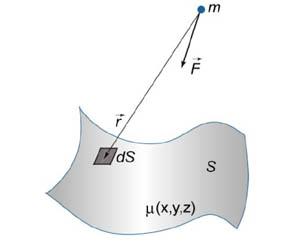
Работа поля
Работа при перемещении
тела в силовом поле ![]() вдоль
кривойC выражается
через криволинейный интеграл второго
рода
вдоль
кривойC выражается
через криволинейный интеграл второго
рода
![]()
где ![]() −
сила, действующая на тело,
−
сила, действующая на тело,![]() −
единичный касательный вектор (рисунок
1). Обозначение
−
единичный касательный вектор (рисунок
1). Обозначение![]() означает
скалярное произведение
векторов
означает
скалярное произведение
векторов![]() и
и![]() .
Заметим,
что силовое поле
.
Заметим,
что силовое поле![]() не
обязательно является причиной движения
тела. Тело может двигаться под действием
другой силы. В таком случае работа
силы
не
обязательно является причиной движения
тела. Тело может двигаться под действием
другой силы. В таком случае работа
силы![]() иногда
может оказаться отрицательной.
Если
векторное поля задано в координатной
форме в виде
иногда
может оказаться отрицательной.
Если
векторное поля задано в координатной
форме в виде
![]()
то работа поля вычисляется по формуле
![]()
В частном случае, когда тело двигается вдоль плоской кривой C в плоскости Oxy, справедлива формула
![]()
где ![]() .
Если
траектория движенияC определена
через параметр t (t часто
означает время), то формула для вычисления
работы принимает вид
.
Если
траектория движенияC определена
через параметр t (t часто
означает время), то формула для вычисления
работы принимает вид

где t изменяется
в интервале от α до β.
Если
векторное поле ![]() потенциально,
то работа по перемещению тела из точки A в
точку B выражается
формулой
потенциально,
то работа по перемещению тела из точки A в
точку B выражается
формулой
![]()
где ![]() −
потенциал поля.
−
потенциал поля.
|
|
|
|
|
Рис.1 |
|
Рис.2 |
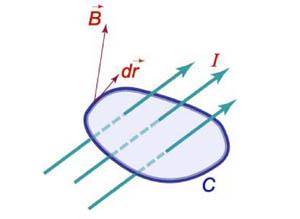
Закон Ампера
Криволинейный
интеграл от магнитного поля с
индукцией ![]() вдоль
замкнутого контураC пропорционален
полному току, протекающему через область,
ограниченную контуром C (рисунок
2). Это выражается формулой
вдоль
замкнутого контураC пропорционален
полному току, протекающему через область,
ограниченную контуром C (рисунок
2). Это выражается формулой
![]()
где ![]() -магнитная
проницаемость ваккуума,
равная
-магнитная
проницаемость ваккуума,
равная ![]() Н/м.
Н/м.
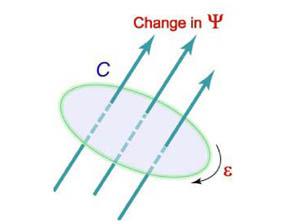
Закон Фарадея
Электродвижущая сила ε, наведенная в замкнутом контуре C, равна скорости изменения магнитного потокаψ, проходящего через данный контур (рисунок 3).
![]()
|
|
|
|
БИЛЕТ51.
ОПРЕДЕЛЕНИЕ. Число
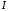 называетсяпределом
интегральных сумм
называетсяпределом
интегральных сумм
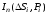 при
при (обозначают
(обозначают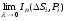 ),
если для любого
),
если для любого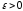 существует
существует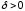 такое, что для любого разбиения
поверхности
такое, что для любого разбиения
поверхности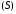 у которого
у которого ,
при любом выборе точек
,
при любом выборе точек выполняется неравенство
выполняется неравенство .
.
Если
существует конечный предел интегральных
сумм
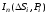 при
при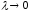 ,
то его называютповерхностным
интегралом I
рода (по площади поверхности)
от функции
,
то его называютповерхностным
интегралом I
рода (по площади поверхности)
от функции
 по поверхности
по поверхности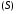 .
.
Поверхностный
интеграл I
рода от функции
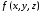 по поверхности
по поверхности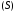 обозначают
обозначают

(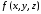 называют подынтегральной функцией,
называют подынтегральной функцией, – областью интегрирования,
– областью интегрирования,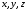 – переменные интегрирования,
– переменные интегрирования, – дифференциал площади поверхности).
– дифференциал площади поверхности).
Если
существует
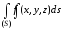 ,
то функция
,
то функция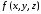 называетсяинтегрируемой
по поверхности
называетсяинтегрируемой
по поверхности
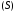 .
.
Достаточное условие существования поверхностного интеграла I рода будет сформулировано позже, когда покажем способ его вычисления.
Определение поверхностного интеграла I рода по структуре такое же, как и определение определенного интеграла. Поэтому поверхностный интеграл I рода обладает теми же свойствами, что и определенный интеграл. Приведем эти свойства без доказательства.
СВОЙСТВА ПОВЕРХНОСТНОГО ИНТЕГРАЛА I РОДА
1.
 ,
где
,
где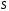 – площадь поверхности
– площадь поверхности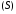 .
.
2.
Постоянный множитель можно выносить
за знак поверхностного интеграла I
рода, т.е. 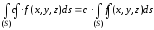 .
.
3. Поверхностный интеграла I рода от алгебраической суммы двух (конечного числа) функций равен алгебраической сумме поверхностных интегралов I рода от этих функций, т.е.
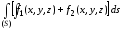
 .
.
4.
Если поверхность
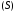 разбита на две части
разбита на две части и
и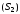 ,
не имеющие общих внутренних точек, то
,
не имеющие общих внутренних точек, то
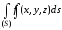

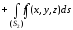
(свойство аддитивности поверхностного интеграла I рода).
5.
Если всюду на поверхности
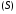 функция
функция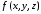
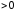 (
(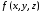
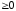 ),
то
),
то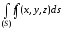
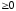 .
.
6.
Если всюду на поверхности
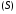

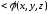 (
(
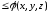 ),
),
то 

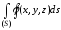 .
.
7.
(следствие свойств 6 и 1) Если
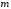 и
и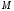 – соответственно наименьшее и наибольшее
значения функции
– соответственно наименьшее и наибольшее
значения функции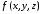 на поверхности
на поверхности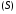 ,
то
,
то
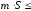

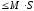 ,
,
где
 – площадь поверхности
– площадь поверхности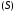 .
.
8.
(теорема о среднем для поверхностного
интеграла I
рода) Если функция
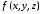 непрерывна на поверхности
непрерывна на поверхности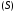 1,
то найдется такая точка
1,
то найдется такая точка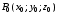
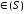 ,
что справедливо равенство
,
что справедливо равенство

 ,
,
где
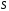 – площадь поверхности
– площадь поверхности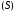 .
.
БИЛЕТ52
Рассмотрим
скалярную функцию ![]() и
поверхностьS.
Пусть S задана
векторной функцией
и
поверхностьS.
Пусть S задана
векторной функцией
![]()
где
координаты (u,v) изменяются
в пределах некоторой области определения ![]() в
плоскостиuv.
Заметим, что функция
в
плоскостиuv.
Заметим, что функция ![]() рассматривается
только в точках, принадлежащих
поверхностиS,
то есть
рассматривается
только в точках, принадлежащих
поверхностиS,
то есть
![]()
Поверхностный
интеграл первого рода от
функции ![]() по
поверхностиS определяется
следующим образом:
по
поверхностиS определяется
следующим образом:
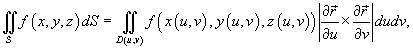
где
частные производные ![]() и
и![]() равны
равны
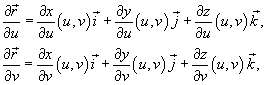
а ![]() означает
векторное произведение. Вектор
означает
векторное произведение. Вектор![]() перпендикулярен
поверхности в точке
перпендикулярен
поверхности в точке![]() .
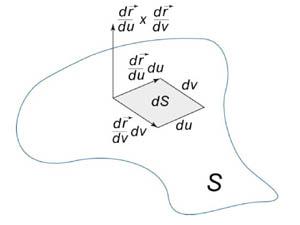
Абсолютное
значение
.
Абсолютное
значение 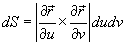 называетсяэлементом
площади:
оно соответствует изменению площади dS в
результате приращения координат u и v на
малые значения du и dv (рисунок
1).
называетсяэлементом
площади:
оно соответствует изменению площади dS в
результате приращения координат u и v на
малые значения du и dv (рисунок
1).
|
|
|
|
|
Рис.1 |
|
Рис.2 |
Площадь поверхности S выражается с помощью поверхностного интеграла в виде
![]()
Если
поверхность S задана
уравнением ![]() ,
гдеz (x,y) −
дифференцируемая функция в области D (x,y),
то поверхностный интеграл находится
по формуле
,
гдеz (x,y) −
дифференцируемая функция в области D (x,y),
то поверхностный интеграл находится
по формуле
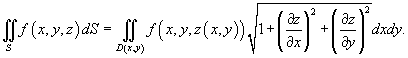
Если поверхность S состоит из нескольких частей Si, то для вычисления поверхностного интеграла можно использовать свойство аддитивности:
![]()
|
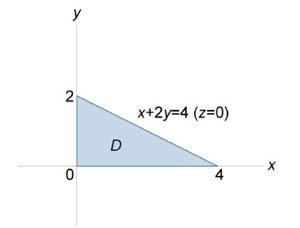
Пример 1 | ||||||
|
| ||||||
|
Вычислить
поверхностный интеграл Решение. Запишем уравнение плоскости в виде
Найдем частные производные
Применяя формулу
поверхностный интеграл можно выразить через двойной интеграл:
Область интегрирования D представляет собой треугольник, показанный выше на рисунке 2. Вычисляем окончательно заданный интеграл:
БИЛЕТ53. Поверхностные интегралы применяются во многих прикладных расчетах. В частности, с их помощью вычисляются
Масса оболочки Пусть S представляет
собой тонкую гладкую оболочку.
Распределение массы оболочки описывается
функцией плотности
Центр масс и моменты инерции оболочки Пусть
распределение массы m в
тонкой оболочке описывается непрерывной
функцией плотности
где
− так называемые моменты первого порядка относительно координатных плоскостей x = 0, y = 0 и z = 0, соответственно. Моменты инерции оболочки относительно осей Ox, Oy, Oz выражаются, соответственно, формулами
Моменты инерции оболочки относительно плоскостей xy, yz, xz определяются формулами
Сила притяжения поверхности Пусть задана поверхность S, а в точке (x0, y0, z0), не принадлежащей поверхности, находится тело массой m(рисунок 1).
Сила притяжения между поверхностью S и точечным телом m определяется выражением
где Сила давления
Предположим,
что поверхность S задана
вектором
Давление, по определению, действует в направлении вектора нормали к поверхности S в каждой точке. Поэтому, мы можем записать
где Поток жидкости и поток вещества
Если
в качестве векторного поля рассматривается
скорость жидкости
Аналогично,
поток векторного поля
Он численно равен массе вещества, проходящего через поверхность S в единицу времени. Заряд поверхности
Пусть
величина
Теорема Гаусса
Поток
электрического смещения
где БИЛЕТ54 Одной из основных характеристик поверхности является её нормаль — единичный вектор, перпендикулярный касательной плоскости в заданной точке:
Знак нормали зависит от выбора координат. Ориентация Также важной характеристикой поверхности является её ориентация. Поверхность называется двусторонней, если на всей её протяжённости она обладает непрерывным вектором нормали. В противном случае поверхность называют односторонней. Ориентированной называется двусторонняя поверхность с выбранным направлением нормали.
|
БИЛЕТ55.
Свойства:
1) линейность
Если вместо P возьмем линейную функцию (f+g), то интеграл будет линейной комбинаций.
Примечание определение поверхности второго интеграла второго рода было дано, когда ориентация поверхности такова, что выбранная нормаль к поверхности составляет острый угол с положительным направлением оси OZ.
В случае, если этот угол тупой все пределы интегрирования сумм Дарбу должны быть взяты со знаком «минус».
2) аддитивность
поверхностный интеграл второго рода по поверхности, являющейся суммой двух поверхностей, которые одинаково ориентированы и имеют общую границу площади О равную сумме поверхностных интегралов второго рода по каждой из поверхностей.
3) при изменении ориентации поверхности, поверхностный интеграл меняет знак.
4) для поверхностного интеграла второго рода не выполняется теорема о среднем.
Определение:
Рассмотрим двустороннюю
поверхность ![]() ,
гладкую или кусочно-гладкую, и фиксируем
какую-либо из двух ее сторон, что
равносильно выбору на поверхности
определенной ориентации.
,
гладкую или кусочно-гладкую, и фиксируем
какую-либо из двух ее сторон, что
равносильно выбору на поверхности
определенной ориентации.
Для
определенности предположим сначала,
что поверхность задана явным
уравнением ![]() причем
точка
причем
точка ![]() изменяется
в области
изменяется
в области ![]() на
плоскости
на
плоскости ![]() ,
ограниченный кусочно-гладким контуром.
,
ограниченный кусочно-гладким контуром.
Пусть
теперь в точках данной поверхности ![]() определена
некоторая функция
определена
некоторая функция ![]() .
Разбив поверхность сетью кусочно-гладких
кривых на части
.
Разбив поверхность сетью кусочно-гладких
кривых на части ![]() и
выбрав на каждой такой части
точку
и
выбрав на каждой такой части
точку ![]() вычисляем
значение функции
вычисляем
значение функции ![]() в
данной точке и умножим его на
площадь
в
данной точке и умножим его на
площадь ![]() проекции
на плоскость
проекции
на плоскость ![]() элемента
элемента ![]() ,
снабженную определенным знаком. Составим
интегральную сумму:
,
снабженную определенным знаком. Составим
интегральную сумму:
![]() .
.
Конечный предел этой интегральной суммы при стремлении диаметров всех частей к нулю называют поверхностным интегралом второго рода от
![]() ,
,
распространенным
на выбранную сторону поверхности ![]() ,
и обозначают символом
,
и обозначают символом
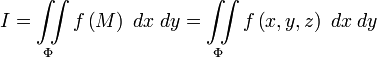
(здесь ![]() )
напоминает о площади проекции элемента
поверхности на плоскость
)
напоминает о площади проекции элемента
поверхности на плоскость ![]()
Если
вместо плоскости ![]() спроектировать
элементы поверхности на плоскость
спроектировать
элементы поверхности на плоскость ![]() или
или ![]() ,
то получим два других поверхностных
интеграла второго типа:
,
то получим два других поверхностных
интеграла второго типа:
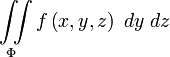 или
или 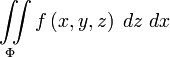 .
.
В приложениях чаще всего встречаются соединения интегралов всех этих видов:
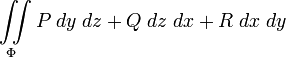
где ![]() суть
функции от
суть
функции от ![]() ,
определенные в точках поверхности
,
определенные в точках поверхности ![]() .
.
БИЛЕТ56.
Вычисление поверхностных интегралов второго рода.
Поверхностные интегралы второго рода вычисляют сведением их к двойным интегралам.
Пусть ориентированная гладкая .поверхность S задана уравнением z==f(х,у), где функция f(х, у) определена в замкнутой области G — проекции поверхности S на плоскость Оху, а R(х,у,z)непрерывная функция на поверхности S.
Разобьем поверхность S произвольно на n частей и спроектируем это разбиение на плоскость Оху. Область G разобьется соответственно на частиG1,G2 ... Gn. Выберем на каждой части поверхности произвольную точку М(ξi ηi ςi) и составим интегральную сумму ∑I=1nR(ξi ηi ςi)ΔSi где, ΔSi площадь Gi Так как ςi=f(ξi ηi), то ∑I=1nR(ξi ηi ςi)ΔSi=∑I=1nR[ξi ηi f f(ξi ηi)]ΔSi—1
В правой части равенства находится интегральная сумма для двойного интеграла от непрерывной в области G функции R[х, у, f(х, у)]. Переходя к пределу в (1) при λ→0, получаем искомую формулу ⌠⌠S R(x,y,z)dxdy=⌠⌠S R(x,y,f(x,y)]dxdy—2- выражающую поверхностный интеграл второго рода по переменным х и у через двойной. Кроме того, формула (2) доказывает существование поверхностного интеграла от функции К (х, у, z), непрерывной на рассматриваемой поверхности S. Если выбрать нижнюю сторону поверхности, то перед интегралом в правой части (2) появится знак минус.
Аналогично устанавливается справедливость следующих формул: ⌠⌠S P(x,y,z)dydz=⌠⌠S P(x,y,f(x,y)]dydz ; ⌠⌠S Q(x,y,z)dzdx=⌠⌠S Q(x,y,f(x,y)]dzdx где поверхность Sзадана соответственно уравнением x=f(у,z) и у=f(x,z), а G1, и G2—проекции поверхности S соответственно на плоскости Оуz и Охz..
Связь между поверхностными интегралами первого и второго рода. Поверхностные интегралы второго рода можно ввести и другим способом, а именно как поверхностные интегралы первого рода, в которых под знаком интеграла стоят некоторые специальные выражения. Обозначим через соа α, соs β, соs γ направляющие косинусы нормали ориентированной поверхности в произвольной ее точке. Поверхностные интегралы второго рода различаются своим отношением к координатным плоскостям:
1) поверхностный интеграл второго рода для плоскости Оху от функции R(х, у, z) выражается через поверхностный интеграл первого рода с помощью следующей формулы: ⌠⌠S R(x,y,z)dxdy=⌠⌠S R(x,y,z) соs γ dS .2) Аналогично ⌠⌠S Q(x,y,z)dxdy=⌠⌠S Q(x,y,z) соs β dS . 3) ⌠⌠S P(x,y,z)dxdy=⌠⌠S P(x,y,z) соs α dS
Суммируя формулы (1)- (3), получаем формулу, выражающую поверхностный интеграл второго рода общего вида по выбранной стороне поверхности через поверхностный интеграл первого рода: ⌠⌠S P dxdy+⌠⌠S Q dxdy+⌠⌠S Rdxdy=⌠⌠S(P соs α+Q соs β+R соs γ)dS. Если выбрать другую сторону поверхности, тонаправляющие косинусы нормали соа α, соs β, соs γ изменят знак и, следовательно, изменит знак поверхностный интеграл второго рода.
БИЛЕТ57.
Поверхность уровня
Скалярное поле можно представить графически с помощью поверхностей уровня (также называемой изоповерхностями).
Поверхностью
уровня скалярного поля ![]() называется
множество точек пространства, в которых
функция u принимает
одно и то же значение c,
то есть поверхность уровня определяется
уравнением
называется
множество точек пространства, в которых
функция u принимает
одно и то же значение c,
то есть поверхность уровня определяется
уравнением ![]() .
Набор поверхностей уровня для разных c дает
наглядное представление о конкретном
скалярном поле, для которого они построены
(изображены)[4],
кроме того, представление о поверхностях
уровня дает определенный дополнительный
геометрический инструмент для работы
со скалярным полем, который может
использоваться для вычислений,
доказательства теорем итп.
Пример: эквипотенциальная
поверхность.
.
Набор поверхностей уровня для разных c дает
наглядное представление о конкретном
скалярном поле, для которого они построены
(изображены)[4],
кроме того, представление о поверхностях
уровня дает определенный дополнительный
геометрический инструмент для работы
со скалярным полем, который может
использоваться для вычислений,
доказательства теорем итп.
Пример: эквипотенциальная
поверхность.
Для поля на двумерном пространстве аналогом поверхности уровня является линии уровня. Примеры: изобата, изотерма, горизонталь на географической карте и прочие изолинии.
Поверхностями уровня для скалярного поля на пространстве большей размерности являются гиперповерхности размерности на единицу меньшей, чем размерность пространства.
Градиент
Направление
скорейшего возрастания
поля ![]() указываетвектор градиента,
обозначаемый стандартно
указываетвектор градиента,
обозначаемый стандартно
![]() ,
,
или
![]() ,
,
с компонентами:
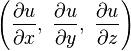 .
.
(Приведена формула для трёхмерного случая, на другие размерности она обобщается прямо и тривиально).
Если координаты не декартовы (базис не ортонормирован) существенно заметить, что приведенные выше компоненты градиента есть компоненты ковариантные, т.е. градиент скалярного поля есть ко-векторное поле. Для ортономированных базисов это не существенно, так как для них понятие вектора и ко-вектора можно считать совпадающими, как и ковариантные и контравариантные координаты.
Абсолютная величина вектора градиента u есть производная u по направлению скорейшего роста (скорость роста u при движении с единичной скоростью в этом направлении).
Градиент всегда перпендикулярен поверхностям уровня (в двумерном случае — линиям уровня). Исключение — особые точки поля, в которых градиент равен нулю.
Производная
скалярного поля по направлению ![]() определяется
как
определяется
как ![]() .
Известно из теории функций многих
переменных ,чтопроизводная
по направлению есть проекция градиента
на данное направление
.
Известно из теории функций многих
переменных ,чтопроизводная
по направлению есть проекция градиента
на данное направление
![]() .
.
Пример. Найти производную скалярного поля g(x, y, z) = x2 + y2 + z3 по направлению {1,3,2} в точке (1,0,4)
![]() .
.
БИЛЕТ58.
Определение 1
Полем называется совокупность значений той или иной величины (скорость, плотность, давление и т.п.), заданных в каждой точке рассматриваемой области.
Если рассматриваемая величина
а) скаляр, то поле называется скалярным, например
![]() –
поле
плотности
–
поле
плотности
б) вектор, то поле называется векторным
![]() –
поле
скоростей
–
поле
скоростей
в) тензор, то поле называется тензорным
![]() –
поле
напряжений.
–
поле
напряжений.
Определение 2
Если
значения рассматриваемых величин не
изменяются во
времени,
то поле называется стационарным (установившимся),
если же они ![]() изменяются во
времени,
то поле называется нестационарным.
изменяются во
времени,
то поле называется нестационарным.
Здесь мы остановимся на рассмотрении свойств стационарных полей.
(если нужны характеристики см.57)
БИЛЕТ59.
Формула Стокса
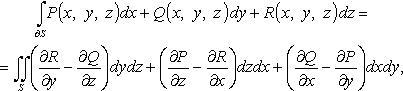
обход
контура ![]() (границы
поверхностиS)
согласован с выбором стороны поверхности S.
(границы
поверхностиS)
согласован с выбором стороны поверхности S.
Формула Стокса в символической форме
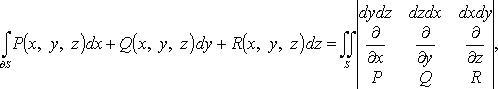
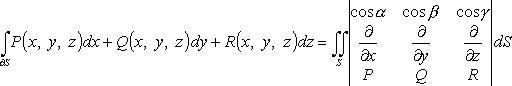
(![]() -
направляющие косинусы нормали,
соответствующей выбранной стороне
поверхности.
-
направляющие косинусы нормали,
соответствующей выбранной стороне
поверхности.
Формула Остроградского
![]()
(![]() -
внешняя сторона поверхности телаE);
-
внешняя сторона поверхности телаE);
![]()
(![]() -
направляющие косинусы внешней нормали
к поверхности
-
направляющие косинусы внешней нормали
к поверхности![]() ).
).
БИЛЕТ60.
Векторное поле — это отображение, которое каждой точке рассматриваемого пространства ставит в соответствиевектор с началом в этой точке. Например, вектор скорости ветра в данный момент времени изменяется от точки к точке и может быть описан векторным полем.
Вариации векторного поля:
Евклидово пространство
Векторное
поле
на евклидовом (или псевдоевклидовом) пространстве[1] ![]() определяется
каквектор-функция точки
пространства, отображающая это
пространство в (на) себя[2]:
определяется
каквектор-функция точки
пространства, отображающая это
пространство в (на) себя[2]:
![]()
То есть, каждой точке пространства сопоставляется некоторый вектор (значение векторного поля в данной точке пространства). В общем случае этот вектор различается для разных точек пространства, то есть в общем случае векторное поле принимает разные значения в разных точках пространства. В каждой точке пространства вектор поля имеет определенную величину и определенное (за исключением тех случаев, когда поле обращается в ноль) направление в этом пространстве[3].
В литературе (особенно в более старой, а также в физической) применительно к векторному полю на некотором пространстве употребляется также предлог в (то есть говорят и поле на пространстве, и поле в пространстве).
Многообразие
В
более общем случае, когда исходное
пространство является многообразием, векторное
поле определяется
как сечение касательного
расслоения к
данному многообразию, то есть отображение,
которое каждой точке ![]() ставит
в соответствие вектор
ставит
в соответствие вектор![]() из
касательного пространства в
из
касательного пространства в![]() .
.
В физике
В физике термин векторное поле, кроме общего значения, описанного выше, имеет специальное значение, в основном в отношении фундаментальных полей (см. ниже). Смысл этого употребления сводится к тому, что фундаментальные физические поля классифицируются по природе их потенциала, и один из таких типов — векторные поля (как электромагнитное или глюонное поля).
Обозначается векторное поле обычно просто в соответствии с соглашениями, принятыми для векторов
в физике для этого обычно используется жирный шрифт или стрелка над буквой, например,
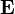 или
или 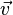 ;
;для 4-векторов — традиционна индексная запись, например
 ;
;
в математической литературе в целом для векторов вообще и векторных полей в частности нет каких-то общепринятых специальных обозначений.
Нередко явно указывается зависимость от точки пространства[4], например:
![]() где
где ![]() —
символическое обозначение точки
пространства,
—
символическое обозначение точки
пространства,
или
![]() где
где ![]() —радиус-вектор,
характеризующий точку пространства.
—радиус-вектор,
характеризующий точку пространства.
Достаточно обычно задание векторного поля как функции координат в пространстве, на котором поле задано, например:
![]()
или (для поля, зависящего от времени):
![]()
Для силовых полей силовые линии наглядно показывают направление воздействия полевых сил.
Если в достаточно малой области пространства поле нигде не обращается в нуль, то через каждую точку этой области проходит одна и только одна силовая линия. Точки, где вектор поля нулевой — особые, в них направление поля не определено, и поведение силовых линий в окрестности этих точек может быть различным: возможно, через особую точку проходит бесконечно много силовых линий, но возможно, что не проходит ни одна.
Векторное поле называется полным, если его интегральные кривые определены на всём многообразии.
БИЛЕТ61
В математике поток векторного поля используется для двух различных понятий:
Поток векторного поля через поверхность (см. ниже)
Фазовый поток — поток векторного поля
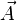 —
однопараметрическое семействодиффеоморфизмов
—
однопараметрическое семействодиффеоморфизмов  ,
определяемых дифференциальным
уравнением
,
определяемых дифференциальным
уравнением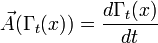 .
.
Поток векторного
поля через
поверхность — поверхностный
интеграл второго
рода по поверхности ![]() .
По определению
.
По определению
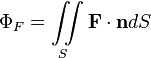
где ![]() —
векторное поле (вектор-функция векторного
аргумента — точки пространства),
—
векторное поле (вектор-функция векторного
аргумента — точки пространства),![]() —единичный
вектор положительной нормали к
поверхности (положительное направление
выбирается для ориентируемой поверхности
условно, но одинаково для всех точек —
то есть для дифференцируемой поверхности —
так, чтобы
—единичный
вектор положительной нормали к
поверхности (положительное направление
выбирается для ориентируемой поверхности
условно, но одинаково для всех точек —
то есть для дифференцируемой поверхности —
так, чтобы ![]() было
непрерывно; для не ориентируемой
поверхности это не важно, так как поток
через неё всегда ноль),
было
непрерывно; для не ориентируемой
поверхности это не важно, так как поток
через неё всегда ноль),![]() —
элемент поверхности.
—
элемент поверхности.
В трёхмерном случае
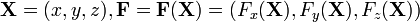 ,
а поверхностью является обычная
двумерная поверхность.
,
а поверхностью является обычная
двумерная поверхность.
Иногда, особенно в физике, применяется обозначение
![]()
тогда поток записывается в виде
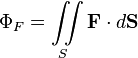 .
.
Физическая интерпретация
Пусть
движение несжимаемой жидкости единичной
плотности в пространстве задано векторным
полем скорости течения ![]() .
Тогда объём жидкости, который протечёт
за единицу времени через поверхность
.
Тогда объём жидкости, который протечёт
за единицу времени через поверхность![]() ,
будет равен потоку векторного поля
,
будет равен потоку векторного поля![]() через
поверхность
через
поверхность![]() .
.
1