
- •1.Комплексные числа. Свойства. Формы записи.
- •2.Интегрирование простейших рациональных функций
- •3)Интегрирование рациональных функций методом неопределённых коэффициентов. Метод Остроградского.
- •4.Интегрирование тригонометрических функций
- •Геометрический смысл несобственного интеграла I рода
- •Примеры
- •13. Несобственный интеграл второго рода
- •15. Схема применения определённого интеграла
- •16. Вычисление площади плоских фигур
- •Вопрос 20
- •Вопрос 21 Формула метода трапеций.
- •Графическая иллюстрация метода парабол (Симпсона).
- •Вопрос 23
- •Вопрос 24
- •37 Приложения двойного интэграла 1. Вычисление площадей
- •2. Вычисление объёмов тел
- •3. Центр тяжести плоской фигуры
- •42 Приложения тройного интэграла . Вычисление объёма тела:
- •2. Вычисление массы тела переменной плотности γ (X; y; z):
- •3. Координаты центра тяжести тела с постоянной плотностью:
- •4. Координаты центра тяжести тела с переменной плотностью γ (X; y; z):
Геометрический смысл несобственного интеграла I рода
Несобственный интеграл первого рода выражает площадь бесконечно длинной криволинейной трапеции.
Примеры
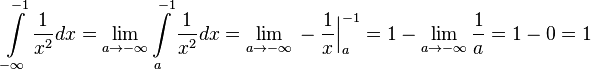
БИЛЕТ13
13. Несобственный интеграл второго рода
Несобственный интеграл второго рода выражает площадь бесконечно высокой криволинейной трапеции
Несобственным интегралом второго рода назовём определенный интеграл
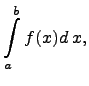
значение которого равняется левостороннему пределу
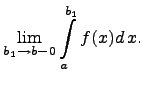
БИЛЕТ14
14. Признаки сходимости несобственных интегралов Первая теорема сравнения
Если ![]() на
на ![]() то
из сходимости
то
из сходимости 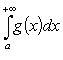 следует
сходимость ,
следует
сходимость ,

Вторая теорема сравнения
Если  то
при
то
при ![]() интегралы
интегралы 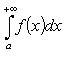 и
и 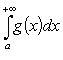 или
оба сходятся, или оба расходятся.
или
оба сходятся, или оба расходятся.
При ![]() из
сходимости
из
сходимости 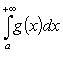 следует
сходимость
следует
сходимость 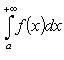
При ![]() из
сходимости
из
сходимости  следует
сходимость
следует
сходимость 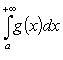
Степенной признак
Если ![]() при
при ![]() то
при
то
при ![]() интеграл
интеграл 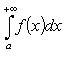 сходится,
сходится,
Признак Абеля
Если  сходится,
а g монотонна
и ограничена на
сходится,
а g монотонна
и ограничена на ![]() то
то 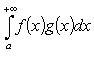 сходится.
сходится.
Признак Дирихле
Если f имеет
ограниченную первообразную
на ![]() а g монотонно
стремится к нулю при
а g монотонно
стремится к нулю при ![]()
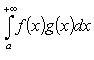 сходится.
сходится.
БИЛЕТ15
15. Схема применения определённого интеграла
Схема называется «метод дифференциала» или «метод отбрасывания бесконечно малых высших порядков»:
1) на отрезке [а;b] выбираем произвольное значение х и рассматриваем переменный отрезок [а; х]. На этом отрезке величина А становится функцией х: А = А(х), т. е. считаем, что часть искомой величины А есть неизвестная функция А(х), где х є [a;b] — один из параметров величины А;
2) находим главную часть приращения ΔА при изменении х на малую величину Δх = dx, т. е. находим дифференциал dA функции А = А(х): dA = ƒ(х) dx, где ƒ(х), определяемая из условия задачи, функция переменной х (здесь также возможны различные упрощения);
3) считая, что dA ≈ ΔА при Δх → 0, находим искомую величину путем интегрирования dA в пределах от а до b:
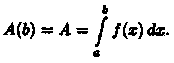
БИЛЕТ16
16. Вычисление площади плоских фигур
Вычисление площадей с помощью интеграла.
1.Площадь фигуры, ограниченной графиком непрерывной отрицательной на промежутке [ a ; b ] функции f (x), осью Ох и прямыми х=а и х= b :

2.Площадь
фигуры, ограниченной графиками непрерывных
функций f (x), ![]() и
прямыми х=а, х= b :
и
прямыми х=а, х= b :
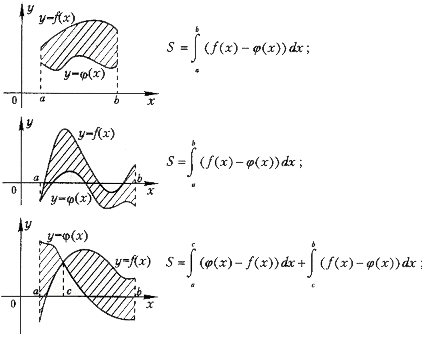
3.Площадь
фигуры, ограниченной графиками непрерывных
функций f (x) и ![]() :
:
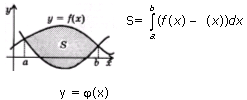
4.Площадь
фигуры, ограниченной графиками непрерывных
функций f (x), ![]() и
осью Ох:
и
осью Ох:
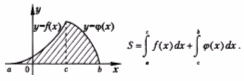
БИЛЕТ17
17. Вычисление дуги плоской кривой
Пусть
известна функция ![]() и
требуется найти длину дуги, заданной
функцией
и
требуется найти длину дуги, заданной
функцией ![]() ,
где
,
где ![]() .
.
Для того, чтобы найти длину дуги, нужно вычислить определённый интеграл
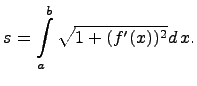
БИЛЕТ18
18. Вычисление
площади поверхности и объёма тела
вращения
-Найдем
площадь поверхности, которая образуется
вращением кривой![]() вокруг
оси
вокруг
оси ![]() ,
где
,
где ![]() .
.
Указанную площадь можно получить вычислением определенного интеграла:
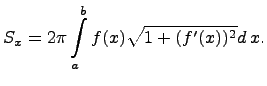
-Тело
образованно
вращением вокруг оси абсцисс криволинейной
трапеции, расположенно в верхней
полуплоскости и ограниченной осью
абсцисс, прямыми ![]() и
и ![]() и
графиком непрерывной функции
и
графиком непрерывной функции ![]() .
.
объем выражается формулой
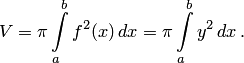
БИЛЕТ19
Вопрос 19
|
Работа силыF=F(x) по перемещению точкиMвдоль осиOxиз положенияx=a, доx=b:
|
Путь,пройденный телом, с скоростьюv(t) за время от t1доt2:
|
Давление жидкости на вертикальную пластинку, ограниченную линиями x=a,x=b,y1=f1(x),y2=f2(x),dжидкость с плотностью(x):
|
|
Масса стержня, расположенного на отрезке [a, b] осиOxс линейной плотностью(x) вычисляется по формуле:
|
Абсцисса xцентра тяжести стержня, расположенного на отрезке [a, b] осиOxс линейной плотностью(x) вычисляется по формуле:
| |
|
Масса дуги кривой y=y(x), проектирующейся на осьOxв виде отрезка [a, b] осиOx,с линейной плотностью(x)вычисляется по формуле:
|
Абсцисса xcи ординатаycцентра тяжести дуги кривойy=y(x), проектирующейся на осьOxв виде отрезка [a, b] осиOx,с постоянной линейной плотностьювычисляется по формуле:
| |
БИЛЕТ20

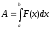 .
(1)
.
(1)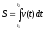 .
(2)
.
(2)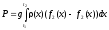 .
(3)
.
(3)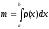 .
(4)
.
(4)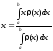 .
(5)
.
(5)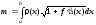 .
(6)
.
(6)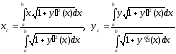 .
(7)
.
(7)