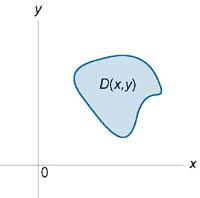37 Приложения двойного интэграла 1. Вычисление площадей

2. Вычисление объёмов тел

Пусть тело V ограничено (рис. 2.12)сверху — только одной поверхностью  z = z_в(x; y); снизу — только одной поверхностью z = z_н(x; y). Линия Lпересечения этих поверхностей проектируется в границу Г области D, на которой заданы непрерывные функции  z = z_в(x; y), z = z_н(x; y).

При этих условиях:

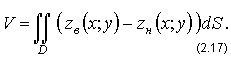
Доказательство формулы (2.17) легко провести на основе геометрического смысла двойного интеграла.

3. Центр тяжести плоской фигуры

Если 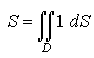   ,   то координатых_c и у_c центра С находятся так:

БИЛЕТ38

38 тройной интэграл основные определения и свойства Рассмотрим кубируемую область в трехмерном пространстве . Разбиение на части осуществляется непрерывными поверхностями. Диаметр разбиения определяется аналогично двумерному случаю. Также, по аналогии, можно определить для функции , разбиения области и выбранных точек интегральную сумму , где обозначает объем области .

Определение. Пусть такое число, что . Тогда мы говорим, что интегрируема на , число есть интеграл по области и обозначаем это так: .

Как и в случае двойного интеграла, выполняются аналогичные свойства 1-6. Можно доказать, что если непрерывна на , то она интегрируема на . Точно также можно убедиться в том, что если точки разрыва лежат на конечном числе непрерывных поверхностей, лежащих в и разбивающих на кубируемые области, то интегрируема на .

Вычисление тройного интеграла производится по следующему правилу.

Теорема. Пусть задана следующими неравенствами: , . - квадрируемая область на плоскости, - непрерывные. Тогда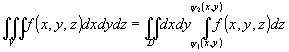 

Замечание. Если область задана неравенствами , где - непрерывные функции, то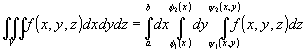 

Сформулируем общую теорему о замене переменных.

Теорема. Пусть отображение устанавливает взаимно однозначное соответствие между областями и , причем функции - непрерывно дифференцируемые и 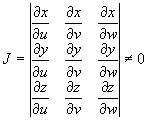ни в одной точке . Пусть - непрерывная на функция. Тогда БИЛЕТ39

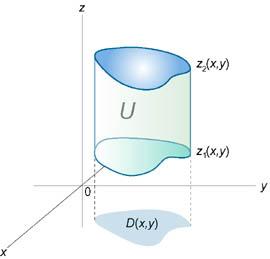
39 вычисление тройного интэграла в декартовых координатах Вычисление тройного интеграла в декартовых координатах сводится к последовательному вычислению трех определенных интегралов.  Рассмотрим случай, когда область интегрирования U является элементарной относительно оси Oz, т.е. любая прямая, параллельная оси Oz, пересекает границу области U не более, чем в двух точках. Пусть областьU ограничена снизу поверхностью z = z₁(x,y), а сверху - поверхностью z = z₂(x,y) (рисунок 1). Проекцией телаU на плоскость Oxy является область D (рисунок 2). Будем предполагать, что функции z₁(x,y) и z₂(x,y)непрерывны в области D.

Рис.1		Рис.2

Тогда для любой непрерывной в области U функции f (x,y,z) можно записать соотношение

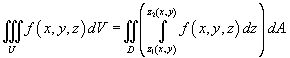
Таким образом, вычисление тройного интеграла сводится к вычислению двойного интеграла, в котором подынтегральной функцией является однократный интеграл. В рассмотренном случае сначала вычисляется внутренний интеграл по переменной z, а затем - двойной интеграл в области D по переменным x и y.  Если область D(x,y) является областью типа I (смотрите Повторные интегралы), т.е. ограничена линиями

где f₁(x), f₂(x) - непрерывные функции в интервале [a,b] и f₁(x) ≤ f₂(x), то, записывая двойной интеграл в виде повторного, получаем

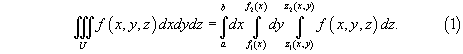
В другом случае, когда область D(x,y) относится к типу II (является элементарной относительно оси Ox) и ограничена линиями

где φ₁(y), φ₂(y) - непрерывные на отрезке [c,d] функции, причем φ₁(y) ≤ φ₂(y), тройной интеграл представляется в виде

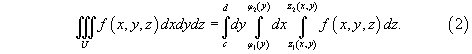
Формулы (1) и (2) называются формулами сведения тройного интеграла к повторному.  В частном случае, когда область интегрирования U представляет собой прямоугольный параллелепипед , тройной интеграл вычисляется по формуле

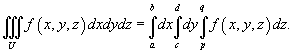
Если исходная область интегрирования U более сложная, чем рассмотренная выше, то ее нужно разбить на конечное число более простых областей, в которых уже можно вычислить тройные интегралы методом сведения к повторным. 

БИЛЕТ40

40 замена переменных в тройном интэграле.цилиндрические координаты При вычислении тройного интеграла, как и двойного, часто удобно сделать замену переменных. Это позволяет упростить вид области интегрирования или подынтегральное выражение.  Пусть исходный тройной интеграл задан в декартовых координатах x, y, z в области U:

Требуется вычислить данный интеграл в новых координатах u, v, w. Взаимосвязь старых и новых координат описывается соотношениями:

Предполагается, что выполнены следующие условия:

1. Функции φ, ψ, χ непрерывны вместе со своими частными производными;

2. Существует взаимно-однозначное соответствие между точками области интегрирования U в пространстве xyz и точками области U' в пространстве uvw;

3. Якобиан преобразования I (u,v,w), равный

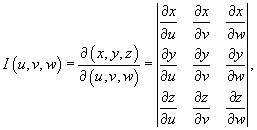
отличен от нуля и сохраняет постоянный знак всюду в области интегрирования U.

Тогда формула замены переменных в тройном интеграле записывается в виде:

В приведенном выражении означает абсолютное значение якобиана.  Для вычисления тройных интегралов часто используютсяцилиндрические и сферические координаты. Эти случаи рассматриваются подробно на страницах

• Тройные интегралы в цилиндрических координатах

• Тройные интегралы в сферических координатах

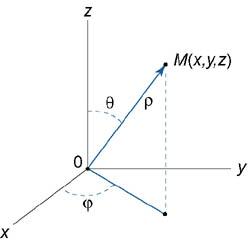
• В цилиндрических координатах положение точки M(x,y,z) в пространстве Oxyz определяется тремя числами −ρ, φ, z , где ρ − длина радиуса-вектора проекции точки M на плоскость Oxy, φ − угол, образованный этим радиусом-вектором с осью Ox (рисунок 1), z − проекция на ось Oz (ее значение одинаково в декартовых и цилиндрических координатах).

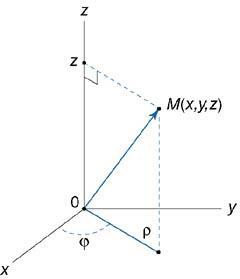
  Рис.1

• Цилиндрические координаты точки связаны с ее декартовыми координатами соотношениями

• 

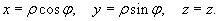
• Здесь предполагается, что

• 

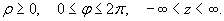
• Якобиан перехода от декартовых координат к цилиндрическим равен

• 

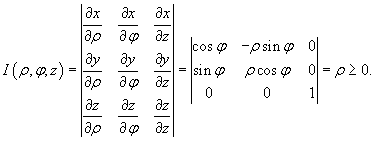
• Тогда формула замены переменных при данном преобразовании имеет вид:

• 

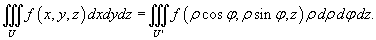
• Переход к цилиндрическим координатам упрощает вычисление тройного интеграла в случаях, когда область интегрирования образована цилиндрической поверхностью. 

БИЛЕТ41

41 замена переменных в тройном интэграле .сферические координатыСферическими координатами точки M(x,y,z) называются три числа − ρ, φ, θ , где 

ρ − длина радиуса-вектора точки M; φ − угол, образованный проекцией радиуса-вектора на плоскостьOxy и осью Ox; θ − угол отклонения радиуса-вектора от положительного направления осиOz (рисунок 1).

Рис.1

Обратите внимание, что определения ρ, φ в сферических и цилиндрических координатах отличаются друг от друга.  Сферические координаты точки связаны с ее декартовыми координатами соотношениями

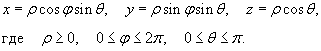
Якобиан перехода от декартовых координат к сферическим имеет вид:

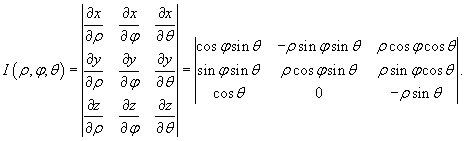
Раскладывая определитель по второму столбцу, получаем

Соответственно, абсолютное значение якобиана равно

Следовательно, формула замены переменных при преобразовании декартовых координат в сферические имеет вид:

Тройной интеграл удобнее вычислять в сферических координатах, когда область интегрирования Uпредставляет собой шар (или некоторую его часть) и/или когда подынтегральное выражение имеет видf (x² + y² + z²).  Иногда выгодно использовать т.н. обощенные сферические координаты, связанные с декартовыми формулами

В этом случае якобиан равен

БИЛЕТ42