
- •1.Комплексные числа. Свойства. Формы записи.
- •2.Интегрирование простейших рациональных функций
- •3)Интегрирование рациональных функций методом неопределённых коэффициентов. Метод Остроградского.
- •4.Интегрирование тригонометрических функций
- •Геометрический смысл несобственного интеграла I рода
- •Примеры
- •13. Несобственный интеграл второго рода
- •15. Схема применения определённого интеграла
- •16. Вычисление площади плоских фигур
- •Вопрос 20
- •Вопрос 21 Формула метода трапеций.
- •Графическая иллюстрация метода парабол (Симпсона).
- •Вопрос 23
- •Вопрос 24
- •37 Приложения двойного интэграла 1. Вычисление площадей
- •2. Вычисление объёмов тел
- •3. Центр тяжести плоской фигуры
- •42 Приложения тройного интэграла . Вычисление объёма тела:
- •2. Вычисление массы тела переменной плотности γ (X; y; z):
- •3. Координаты центра тяжести тела с постоянной плотностью:
- •4. Координаты центра тяжести тела с переменной плотностью γ (X; y; z):
Вопрос 24
Пусть
задана функция f(x,
y).
Тогда каждая из ее частных
производных(если
они, конечно, существуют) ![]() и
и ![]() ,
которые называются также частными
производными первого порядка,
снова являются функцией независимых
переменных x,
y и
может, следовательно также иметь частные
производные. Частная производная
,
которые называются также частными
производными первого порядка,
снова являются функцией независимых
переменных x,
y и
может, следовательно также иметь частные
производные. Частная производная 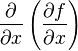 обозначается
через
обозначается
через ![]() или
или ![]() ,
а
,
а 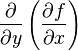 через
через ![]() или
или ![]() .
Таким образом,
.
Таким образом,
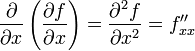 ,
, 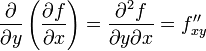
и, аналогично,
 ,
, 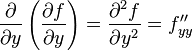 .
.
Производные ![]() и
и ![]() называются частными
производными второго порядка. Определение:Частной
производной второго порядка от функции
z=f(x;y) дифференцируемой в области
D,называется первая производная от
соответствующей частной производной.
Рассматривая частные производные от
них, получим всевозможные частные
производные 3 порядка:
называются частными
производными второго порядка. Определение:Частной
производной второго порядка от функции
z=f(x;y) дифференцируемой в области
D,называется первая производная от
соответствующей частной производной.
Рассматривая частные производные от
них, получим всевозможные частные
производные 3 порядка: ![]() ,
, ![]() ,
, ![]() и т. д.
и т. д.
БИЛЕТ25
25. Дифференцируемость и полный дифференциал функции двух переменных. Теорема о равенстве смешанных производных высших порядков.
Пусть
функция![]() определена в некоторой окрестности
точки
определена в некоторой окрестности
точки![]() . Составим полное приращение функции в
точке М:
. Составим полное приращение функции в
точке М:
![]()
Функция![]() называется дифференцируемой в точке
называется дифференцируемой в точке![]() ,
если её полное приращение в этой точке
можно представить в виде
,
если её полное приращение в этой точке
можно представить в виде
![]() (1)
(1)
где
![]() и
и![]() при
при![]() ,
,
![]() . Сумма первых двух слагаемых в равенстве
(1) представляет собой главную часть
приращения функции..
. Сумма первых двух слагаемых в равенстве
(1) представляет собой главную часть
приращения функции..
Главная
часть приращения функции![]() , линейная относительно
, линейная относительно![]() и
и![]() ,
называется полным дифференциалом этой
функции и обозначается символом
,
называется полным дифференциалом этой
функции и обозначается символом![]() :
:
![]() (2)
(2)
Выражения
![]() и
и![]() называют
частными дифференциалами. Для независимых
переменных х и у полагают
называют
частными дифференциалами. Для независимых
переменных х и у полагают![]() и
и![]() . Поэтому равенство (2) можно переписать
в виде
. Поэтому равенство (2) можно переписать
в виде
![]() (3)
(3)
Теорема
1 (необходимое условие дифференцируемости
функции). Если функция
![]() дифференцируема
в точке М(х,у), то она непрерывна в этой
точке, имеет в ней частные производные
дифференцируема
в точке М(х,у), то она непрерывна в этой
точке, имеет в ней частные производные![]() и
и![]() , причем
, причем![]()
![]()
Так
как функция дифференцируема в точке М,
то имеет место равенство (1). Отсюда
вытекает, что
![]()
Это
означает, что функция непрерывна в точке
М. Положив
![]() в
равенстве (1), получим:
в
равенстве (1), получим:![]() Отсюда находим
Отсюда находим![]() Переходя к пределу при
Переходя к пределу при![]() , получим
, получим![]() т.
е.
т.
е.![]() Таким
образом, в точке М существует частная
производная
Таким
образом, в точке М существует частная
производная![]() Аналогично показывается, что в точке М
существует частная производная
Аналогично показывается, что в точке М
существует частная производная![]()
Равенство (1) можно записать в виде
![]() (4)
(4)
где
![]() при
при![]() ,
,
![]() .
.
Отметим,
что обратное утверждение не верно, т.
е. из непрерывности функции или
существования частных производных не
следует дифференцируемость функции.
Так, непрерывная функция![]() не дифференцируема в точке (0;0).
не дифференцируема в точке (0;0).
Как следствие теоремы получаем формулу для вычисления полного дифференциала. Формула (3) принимает вид:
![]() (5)
(5)
или
![]()
где![]()
![]() – частные дифференциалы функции
– частные дифференциалы функции![]() .
.
Теорема
2 (достаточное условие дифференцируемости
функции).Если функция
![]() имеет непрерывные частные производные
имеет непрерывные частные производные![]() и
и![]() в точке М(х, у), то она дифференцируема
в этой точке и её полный дифференциал
выражается формулой (5).
в точке М(х, у), то она дифференцируема
в этой точке и её полный дифференциал
выражается формулой (5).
Отметим,
что для функции
![]() одной переменной существование
производной
одной переменной существование
производной![]() в точке является необходимым и достаточным
условием её дифференцируемости в этой
точке.
в точке является необходимым и достаточным
условием её дифференцируемости в этой
точке.
Чтобы
функция
![]() была дифференцируема в точке, необходимо,
чтобы она имела в ней частные производные,
и достаточно, чтобы она имела в точке
непрерывные частные производные.
была дифференцируема в точке, необходимо,
чтобы она имела в ней частные производные,
и достаточно, чтобы она имела в точке
непрерывные частные производные.
Арифметические свойства и правила исчисления дифференциалов функции одной переменной сохраняются и для дифференциала функции двух (и большего числа) переменных.
Из
определения дифференциала функции
![]() следует, что при достаточно малых
следует, что при достаточно малых![]() и
и![]() имеет
место приближенное равенство
имеет
место приближенное равенство
![]() (6)
(6)
Так
как полное приращение
![]() равенство (6) можно переписать в следующем
виде:
равенство (6) можно переписать в следующем
виде:
![]() (7)
(7)
Формулой (7) пользуются в приближенных расчетах.
Отметим, что с помощью полного дифференциала можно найти: границы абсолютной и относительной погрешностей в приближенных вычислениях; приближенное значение полного приращения функции и т. д.
Теорема:
Если в некоторой окрестности точки
![]() функция
функция![]() имеет смешанные частные производные
имеет смешанные частные производные![]() и
и![]() ,
причём эти смешанные частные производные
непрерывны в точке
,
причём эти смешанные частные производные
непрерывны в точке![]() , то они равны в этой точке:
, то они равны в этой точке:![]()
![]()
БИЛЕТ26
26.Пусть функция
![]() зависит от переменной
зависит от переменной![]() и дифференцируема в точке
и дифференцируема в точке![]() .
Может оказаться, что в точке
.
Может оказаться, что в точке![]() дифференциал
дифференциал![]() ,
рассматриваемый как функция от
,
рассматриваемый как функция от![]() ,
есть также дифференцируемая функция.
Тогда существует дифференциал от
дифференциала
,
есть также дифференцируемая функция.
Тогда существует дифференциал от
дифференциала![]() данной функции, который называется
дифференциалом второго порядка функции
данной функции, который называется
дифференциалом второго порядка функции![]() .
Дифференциал второго порядка обозначается
следующим образом:
.
Дифференциал второго порядка обозначается
следующим образом:
![]()
Аналогично определяются дифференциалы более высоких порядков.
Определение:
Дифференциалом
![]() -го порядка
-го порядка![]() функции
функции![]() называется дифференциал от дифференциала
называется дифференциал от дифференциала![]() -го
порядка этой функции, то есть
-го
порядка этой функции, то есть![]()
Сложная функция – это функция, аргументом которой также является функция.
С нашей точки зрения, это определение наиболее понятно. Условно можно обозначать как f(g(x)). То есть, g(x) как бы аргумент функции f(g(x)).
К
примеру, пусть f – функция арктангенса,
а g(x) = lnx есть функция натурального
логарифма, тогда сложная функция f(g(x))
представляет собой arctg(lnx). Еще пример:
f – функция возведения в четвертую
степень, а
![]() - целая рациональная функция, тогда
- целая рациональная функция, тогда![]() .
.
В
свою очередь, g(x) также может быть сложной
функцией. Например,
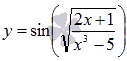 .
Условно такое выражение можно обозначить
как
.
Условно такое выражение можно обозначить
как![]() .
Здесь f – функция синуса, - функция
извлечения квадратного корня,
.
Здесь f – функция синуса, - функция
извлечения квадратного корня,![]() - дробная рациональная функция. Логично
предположить, что степень вложенности
функций может быть любым конечным
натуральным числом
- дробная рациональная функция. Логично
предположить, что степень вложенности
функций может быть любым конечным
натуральным числом![]() .
.
Часто можно слышать, что сложную функцию называют композицией функций.
Формула нахождения производной сложной функции:
![]()
БИЛЕТ27
27.
Пусть имеется поверхность, заданная
уравнением
![]() .
Плоскость, в которой расположены все
касательные прямые к линиям на поверхности,
проходящим через данную точку
.
Плоскость, в которой расположены все
касательные прямые к линиям на поверхности,
проходящим через данную точку![]() ,
называется касательной плоскостью к
поверхности в точке
,
называется касательной плоскостью к
поверхности в точке![]() .
.
Прямая, проведенная через точку поверхности , перпендикулярно к касательной плоскости называется нормалью к поверхности.
Если
поверхность задана уравнением
![]() ,
то уравнение касательной плоскости к
этой поверхности в точке
,
то уравнение касательной плоскости к
этой поверхности в точке![]() записывается в виде:
записывается в виде:
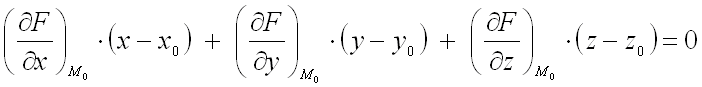
а уравнение нормали к поверхности в этой же точке – в виде:
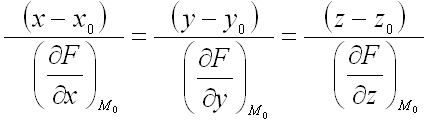
БИЛЕТ28
28. Пусть функция F(t) в некоторой окрестности V(t0) имеет производные до (n+1)-го порядка включительно. Тогда справедлива формула Тейлора:
![]()
![]() (8)
(8)
Обозначим t-t0=Δt, F(t)-F(t0)=ΔF(t0),
F'(t0)(t-t0)=F'(t0)Δt=dF(t0),
F''(t0)(t-t0)2=F''(t0)(Δt)2=d2F(t0) и т.д. Геометрический смысл теоремы Ролля Курс лекций по математике
Тогда (8) можно записать в виде
![]()
, где 0<θ<1. (9)
В виде (9) формула Тейлора распространяется и на случай функций нескольких переменных.
Теорема.
Пусть функция z=f(x;y), где х, у – независимые
переменные, определена и имеет непрерывные
частные производные до (n+1)-го порядка
включительно в некоторой окрестности
точки М(х0;y0) Vδ(х0;y0). Тогда "Δх, Δу,
удовлетворяющих условию
![]() ,
имеет место формула Тейлора:
,
имеет место формула Тейлора:
![]()
![]()
где 0<θ<1. (10)
Доказательство.
Зафиксируем
Δх, Δу:![]() , где
, где
![]() .
.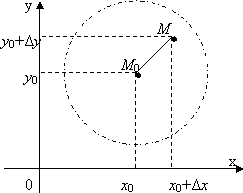
Тогда ММ0ÎVδ(х0;y0). Параметрические уравнения отрезка ММ0:
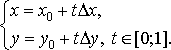 (11)
(11)
Функция на [0;1] становится сложной функцией от переменной t:
f(x;y)=f(х0+tΔx;y0+tΔy)=F(t). (12)
По условию f(x;y) имеет непрерывные частные производные до (n+1)-го порядка включительно на Vδ(х0;y0). Функции х и у, как линейные, имеют непрерывные производные любого порядка. Поэтому F(t) имеет непрерывные производные до (n+1)-го порядка включительно на [0;1]. Тогда для F(t) на [0;1] справедлива формула Тейлора (9).Положим в ней t0=1, t0+Δt=1, Δt=1:
![]() (13)
(13)
Перейдем здесь к f(x;y), используя (12).
ΔF(0)=F(1)-F(0)=f(х0+Δx;y0+Δy)-f(х0;y0)=Δf(х0;y0).
Форма первого дифференциала инвариантна. Тогда, учитывая (11) при вычислении dx и dy, получим
![]()
![]() т.к. dt=Δt=1.
т.к. dt=Δt=1.
Поскольку х=х0+tΔx, y=y0+tΔy – линейные функции, то дифференциалы высших порядков от функции F(t)=f(x;y) обладают свойством инвариантности.. Следовательно, для их вычисления мы можем использовать простейшую форму:
![]()
![]()
Аналогично,
![]() ,…,
,…,![]() ,
,
![]()
Подставляя все выражения в (13), получим (10).
Формула Тейлора имеет большое значение при вычислении приращений и значений функции с большой степенью точности.
БИЛЕТ29
29.Говорят, что функция
![]() имеет максимум в точке
имеет максимум в точке![]() ,
т.е. при
,
т.е. при![]() , если
, если![]() для всех точек
для всех точек![]() ,
достаточно близких к точке
,
достаточно близких к точке![]() и отличных от неё.
и отличных от неё.
Говорят,
что функция
![]() имеет минимум в точке
имеет минимум в точке![]() ,
т.е. при
,
т.е. при![]() ,
если
,
если![]() для всех точек
для всех точек![]() ,
достаточно близких к точке
,
достаточно близких к точке![]() и отличных от неё.
и отличных от неё.
Максимум и минимум функции называются экстремумами функции.
Теорема
(необходимое условие экстремума функции
двух переменных). Если функция
![]() достигает экстремума при
достигает экстремума при![]() ,
то каждая частная производная первого
порядка от
,
то каждая частная производная первого
порядка от![]() или обращается в нуль при этих значениях
аргументов, или не существует.
или обращается в нуль при этих значениях
аргументов, или не существует.
Теорема
(достаточное условие экстремума функции
двух переменных). Пусть в некоторой
области, содержащей точку
![]() функция
функция![]() имеет непрерывные частные производные
до третьего порядка включительно. Пусть,
кроме того, точка
имеет непрерывные частные производные
до третьего порядка включительно. Пусть,
кроме того, точка![]() является критической точкой функции
является критической точкой функции![]() ,
т.е.
,
т.е.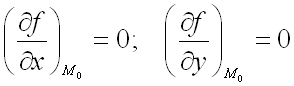
тогда
при
![]() :
:
1)
![]() имеет
максимум, если дискриминант
имеет
максимум, если дискриминант![]() и
и![]() где
где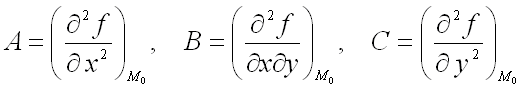
2)
![]() имеет
минимум, если дискриминант
имеет
минимум, если дискриминант![]() и
и![]() ;
;
3)
![]() не
имеет ни минимума, ни максимума, если
дискриминант
не
имеет ни минимума, ни максимума, если
дискриминант![]() ;
;
4)
если
![]() , то экстремум может быть, а может и не
быть (требуется дополнительное
исследование).
, то экстремум может быть, а может и не
быть (требуется дополнительное
исследование).
БИЛЕТ30
30. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ— математический (математико-статистический) прием, служащий для выравнивания динамических рядов, выявления формы корреляционной связи между случайными величинами и др. Состоит в том, что функция, описывающая данное явление, аппроксимируется более простой функцией. Причем последняя подбирается с таким расчетом, чтобы среднеквадратичное отклонение фактических уровней функции в наблюдаемых точках от выровненных было наименьшим.
Напр., по имеющимся данным (xi,yi) (i = 1, 2, ..., n) строится такая кривая y = a + bx, на которой достигается минимум суммы квадратов отклонений
![]()
т. е. минимизируется функция, зависящая от двух параметров: a — отрезок на оси ординат и b — наклон прямой.
Уравнения, дающие необходимые условия минимизации функции S(a,b), называются нормальными уравнениями.
В качестве аппроксимирующих функций применяются не только линейная (выравнивание по прямой линии), но и квадратическая, параболическая, экспоненциальная и др.
БИЛЕТ37
