
- •1.Комплексные числа. Свойства. Формы записи.
- •2.Интегрирование простейших рациональных функций
- •3)Интегрирование рациональных функций методом неопределённых коэффициентов. Метод Остроградского.
- •4.Интегрирование тригонометрических функций
- •Геометрический смысл несобственного интеграла I рода
- •Примеры
- •13. Несобственный интеграл второго рода
- •15. Схема применения определённого интеграла
- •16. Вычисление площади плоских фигур
- •Вопрос 20
- •Вопрос 21 Формула метода трапеций.
- •Графическая иллюстрация метода парабол (Симпсона).
- •Вопрос 23
- •Вопрос 24
- •37 Приложения двойного интэграла 1. Вычисление площадей
- •2. Вычисление объёмов тел
- •3. Центр тяжести плоской фигуры
- •42 Приложения тройного интэграла . Вычисление объёма тела:
- •2. Вычисление массы тела переменной плотности γ (X; y; z):
- •3. Координаты центра тяжести тела с постоянной плотностью:
- •4. Координаты центра тяжести тела с переменной плотностью γ (X; y; z):
Вопрос 20
Суть метода прямоугольников.
Пусть
функция y
= f(x) непрерывна
на отрезке [a;
b].
Нам требуется вычислить определенный
интеграл 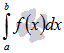 .
.
Обратимся
к понятию
определенного интеграла.
Разобьем отрезок [a;b] на n частей ![]() точками
точками![]() .
Внутри каждого отрезка
.
Внутри каждого отрезка![]() выберем
точку
выберем
точку![]() .
Так как по определению определенный
интеграл есть предел интегральных сумм
при бесконечном уменьшении длины
элементарного отрезка разбиения
.
Так как по определению определенный
интеграл есть предел интегральных сумм
при бесконечном уменьшении длины
элементарного отрезка разбиения![]() ,
то любая из интегральных сумм является
приближенным значением интеграла
,
то любая из интегральных сумм является
приближенным значением интеграла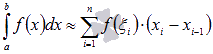 .
.
Суть метода прямоугольников заключается в том, что в качестве приближенного значения определенного интеграла берут интегральную сумму (далее мы покажем, какую именно интегральную сумму берут в методе прямоугольников).
БИЛЕТ21
Вопрос 21 Формула метода трапеций.
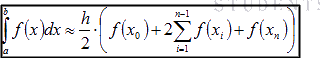
Формула
метода Симпсона (парабол) имеет
вид
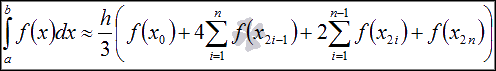 .
.
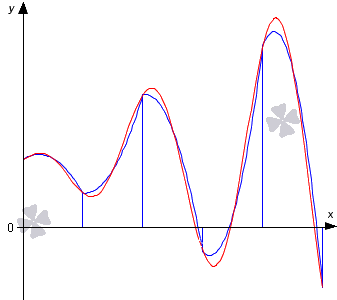
Графическая иллюстрация метода парабол (Симпсона).
Красной линией изображен график функции y=f(x), синей линией показано приближение графика функции y=f(x) квадратичными параболами на каждом элементарном отрезке разбиения.
БИЛЕТ22
Исследование пределов и непрерывности в многомерных пространствах приводит ко многим нелогичным и патологическим результатам, не свойственным функциям одной переменной. Например, существуют скалярные функции двух переменных, имеющих точки в области определения, которые при приближении вдоль произвольной прямой дают специфический предел, и дают другой предел при приближении вдоль параболы. Функция
![]()
стремится
к нулю по любой прямой, проходящей через
начало координат. Однако, когда к началу
координат приближаются вдоль параболы ![]() ,
предел = 0.5. Так как пределы по разным
траекториям не совпадают, предела не
существует.
,
предел = 0.5. Так как пределы по разным
траекториям не совпадают, предела не
существует.
Функция ![]() имеет
пределом число A при стремлении
переменных
имеет
пределом число A при стремлении
переменных![]() ,
соответственно, к
,
соответственно, к![]() ,
если для каждого число
,
если для каждого число![]() найдется
такое число
найдется
такое число![]() ,
что
,
что![]() ,
то есть
,
то есть![]() .
.
Функция ![]() называется
непрерывной в точке
называется
непрерывной в точке![]() ,
если предельное значение этой функции
в точке
,
если предельное значение этой функции
в точке![]() существует
и равно частному значению
существует
и равно частному значению![]() .
.
Функция ![]() называется
непрерывной на множестве
называется
непрерывной на множестве![]() ,
если она непрерывна в каждой точке этого
множества.
,
если она непрерывна в каждой точке этого
множества.
БИЛЕТ23
Вопрос 23
Частная производная обобщает понятие производной на случай нескольких измерений. Частная производная функции нескольких переменных — это производная относительно одной переменной, все другие переменные при нахождении считаются константами.
Для упрощения ограничимся случаем функций от трех переменных; все дальнейшее, однако, справедливо и для функций любого числа переменных.
Пусть
в некоторой области ![]() имеем
функцию
имеем
функцию ![]() ;
возьмем точку
;
возьмем точку ![]() в
этой области. Если мы будем считать
в
этой области. Если мы будем считать ![]() и
и ![]() за
постоянные значения
за
постоянные значения ![]() и
и ![]() ,
и будем менять
,
и будем менять ![]() ,
то
,
то ![]() будет
функцией от одной переменной
будет
функцией от одной переменной ![]() (в
окрестности
(в
окрестности ![]() );
можно поставить вопрос о вычислении ее
производной в точке
);
можно поставить вопрос о вычислении ее
производной в точке ![]() .
Придадим этому значению
.
Придадим этому значению ![]() приращение
приращение ![]() ,
тогда функция получит приращение
,
тогда функция получит приращение ![]() ,
которое можно было бы назвать ее частным
приращением (по
,
которое можно было бы назвать ее частным
приращением (по ![]() ),
поскольку оно вызвано изменением
значения лишь одной переменной. По
самому определению производной, она
представляет собою предел
),
поскольку оно вызвано изменением
значения лишь одной переменной. По
самому определению производной, она
представляет собою предел ![]() .
Эта производная называется частной
производной функции
.
Эта производная называется частной
производной функции ![]() по
по ![]() в
точке
в
точке ![]() .
.
Аналогично
определяются и частные производные
функции ![]() по
по ![]() и
и ![]() в
точке
в
точке ![]() .
Само вычисление частной производной
по существу не представляет ничего
нового по сравнению с вычислением
обыкновенной производной. Частные
производные могут быть объединены
интересными способами для создания
более сложных выражений производных.
В векторном
исчислении оператор
набла (
.
Само вычисление частной производной
по существу не представляет ничего
нового по сравнению с вычислением
обыкновенной производной. Частные
производные могут быть объединены
интересными способами для создания
более сложных выражений производных.
В векторном
исчислении оператор
набла (![]() )
используется для определения
понятий градиента, дивергенции,
и ротора с
точки зрения частных производных.
Матрица частных производных — матрица
Якоби —
может использоваться для представления
производной функции (отображения) между
двумя пространствами произвольной
размерности. Таким образом производная
может быть представлена как линейное
преобразование, которое изменяется в
зависимости от точки из области
определения функции.
)
используется для определения
понятий градиента, дивергенции,
и ротора с
точки зрения частных производных.
Матрица частных производных — матрица
Якоби —
может использоваться для представления
производной функции (отображения) между
двумя пространствами произвольной
размерности. Таким образом производная
может быть представлена как линейное
преобразование, которое изменяется в
зависимости от точки из области
определения функции.
Дифференциальные уравнения, содержащие частные производные, называют дифференциальными уравнениями в частных производных или (Д)УЧП. Эти уравнения как правило сложнее для решения чем обычные дифференциальные уравнения, которые содержат производные относительно только одной переменной.
БИЛЕТ24
