
- •2 Конструирование дощатоклееной балки
- •2.1 Определение нагрузок на раму
- •2.2 Статический расчет рамы
- •2.3 Конструирование дощатоклееной балки
- •2.4 Определение расчетных характеристик древесины
- •2.5 Расчет дощатоклееной балки по первой группе предельных состояний
- •2.5.1 Проверка нормальных напряжений
- •2.5.2 Проверка сдвиговых напряжений
- •2.5.3 Проверка устойчивости плоской формы деформирования
- •2.6 Расчет дощатоклееной балки по второй группе предельных состояний
- •3 Расчет колонны клееной деревянной постоянного сечения
- •3.1 Предварительный подбор сечения колонны
- •3.2 Расчет колонны на прочность
- •3.3 Расчет колонны на устойчивость плоской формы деформирования
- •4 Конструирование узлов
- •4.1 Расчет узла защемления колонны в фундаменте
- •4.2 Расчет опорного узла балки на стойку
- •5 Мероприятия по обеспечению пространственной жесткости и неизменяемости зданий
- •6 Мероприятия по обеспечению долговечности основных несущих и ограждающих конструкций
- •Приложение
2.5 Расчет дощатоклееной балки по первой группе предельных состояний
Максимальный
расчетный изгибающий момент
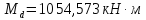 .
Опорная реакция балки
.
Опорная реакция балки
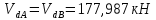 .
.
2.5.1 Проверка нормальных напряжений
Изгибающие напряжения в крайних волокнах, параллельных поверхности, определяем по [1п.3.2]:
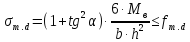
где
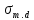 - расчетное напряжение, возникающее в
сечении элемента при изгибе, МПа.
- расчетное напряжение, возникающее в
сечении элемента при изгибе, МПа.
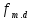 -
расчетное сопротивление древесины
изгибу, МПа.
-
расчетное сопротивление древесины
изгибу, МПа.
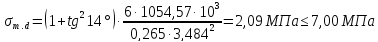
Условие выполняется.
Изгибающие напряжения в крайних волокнах на скатной поверхности, определяем по формуле:

где
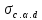 - расчетное напряжение сжатия под углом
- расчетное напряжение сжатия под углом
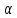 к направлению вдоль волокон;
к направлению вдоль волокон;
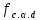 -
расчетное сопротивление древесины
смятию под углом
-
расчетное сопротивление древесины
смятию под углом
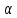 к направлению вдоль волокон.
к направлению вдоль волокон.
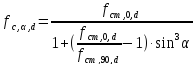

Тогда

Условие выполняется.
2.5.2 Проверка сдвиговых напряжений
При сдвиге в опорном сечении балки проверяем условие [1, формула 23]:
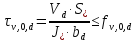
где
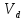 - расчетная поперечная сила;
- расчетная поперечная сила;
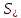 -
статический момент брутто сдвигаемой
части поперечного сечения элемента
относительно нейтральной оси;
-
статический момент брутто сдвигаемой
части поперечного сечения элемента
относительно нейтральной оси;
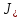 -
момент инерции брутто поперечного
сечения элемента относительно нейтральной
оси;
-
момент инерции брутто поперечного
сечения элемента относительно нейтральной
оси;
 -
расчетная ширина сечения элемента;
-
расчетная ширина сечения элемента;
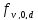 -
расчетное сопротивление древесины
скалыванию при изгибе.
-
расчетное сопротивление древесины
скалыванию при изгибе.
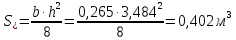

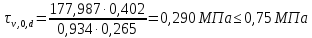
Условие выполняется.
2.5.3 Проверка устойчивости плоской формы деформирования
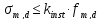
где
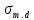 - расчетное напряжение, возникающее в
сечении элемента при изгибе, МПа.
- расчетное напряжение, возникающее в
сечении элемента при изгибе, МПа.
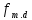 -
расчетное сопротивление древесины
изгибу, МПа.
-
расчетное сопротивление древесины
изгибу, МПа.
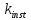 -
коэффициент устойчивости изгибаемого
элемента.
-
коэффициент устойчивости изгибаемого
элемента.
Для
изгибаемых элементов прямоугольного
сечения, шарнирно закрепленных от
смещения из плоскости изгиба и закрепленных
вокруг продольной оси в опорных сечениях,
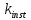 определяют по формуле 22 [1]:
определяют по формуле 22 [1]:
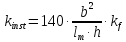
где
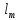 - расстояние между опорными сечениями
элемента, а при закреплении сжатой
кромки элемента в промежуточных точках
от смещения из плоскости изгиба расстояние
между этими точками
- расстояние между опорными сечениями
элемента, а при закреплении сжатой
кромки элемента в промежуточных точках
от смещения из плоскости изгиба расстояние
между этими точками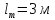 .
.
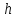 -
максимальная высота поперечного сечения
на участке
-
максимальная высота поперечного сечения
на участке
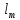 .
.
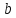 -
ширина поперечного сечения.
-
ширина поперечного сечения.
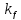 -
коэффициент, зависящий от формы эпюры
изгибающих моментов на участке
-
коэффициент, зависящий от формы эпюры
изгибающих моментов на участке
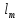 ,
определяем по [1, табл.37].
,
определяем по [1, табл.37].
Согласно
[1, п.3.2] и так как балка имеет линейно
меняющуюся по длине высоту и постоянную
ширину, не имеющую закрепления из
плоскости по растянутой кромке, при
проверке устойчивости изгибаемых
элементов коэффициент
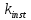 следует умножать на дополнительный
коэффициент
следует умножать на дополнительный
коэффициент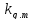 ,
принимаемый по [1, табл.38]:
,
принимаемый по [1, табл.38]:

Тогда:
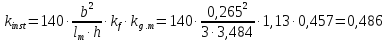
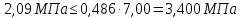
Условие выполняется.
2.6 Расчет дощатоклееной балки по второй группе предельных состояний
Наибольший прогиб Umax изгибаемых элементов переменного сечения определяется по формуле 49 [1]:
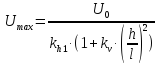
где
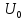 -
прогиб балки постоянного сечения высотой
-
прогиб балки постоянного сечения высотой
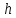 без учета деформаций сдвига;
без учета деформаций сдвига;
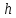 -
наибольшая высота сечения;
-
наибольшая высота сечения;
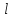 -
пролет балки;
-
пролет балки;
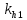 -
коэффициент, учитывающий влияние
переменность высоты сечения;
-
коэффициент, учитывающий влияние
переменность высоты сечения;
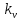 -
коэффициент, учитывающий влияние
деформации сдвига от поперечной силы.
-
коэффициент, учитывающий влияние
деформации сдвига от поперечной силы.
Момент инерции поперечного сечения брутто:
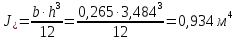
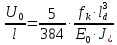
где
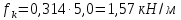 – нормативная нагрузка на 1 м балки.
– нормативная нагрузка на 1 м балки.
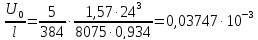
Значение
коэффициентов
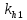 ,
,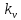 определяем в соответствии с [1, табл.42]:
определяем в соответствии с [1, табл.42]:
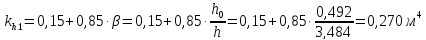
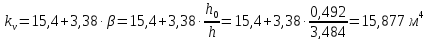
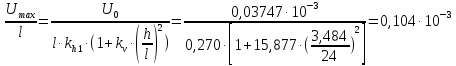
Максимальный относительный прогиб балки пролетом 24 м не должен превышать величины, указанной в [1, табл.41]:
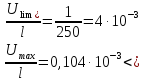
Условие выполняется.
