30. Доверительные интервалы.

Пусть вид распред.изучаемого признака Х известен , но неизвестно значение входящего параметра(тетра).

Оценка неизвестного параметра, кот.задается 2мя числами (концами интервала) наз.интервальной.

Пусть по выборке получена точечн.оценка неизв.пар-тра. Эта оценка тем точнее, чем меньше.

Методы мат.статистики не позволяют наверяка утверждать, что выполняется это нер-во, где .

Можно лишь гов.о вер-сти его выполнения

Величина -наз.доверительной вер-ью или надежностью. В качестве берут число близкое к 1: 0,95; 0,99; 0,995.

Оно выбирается иссл-лем самост-но.Раскрыв знак | | получим опр-ние довер.интервала.

Доверит.наз.интервал , к-ый покрывает неизвестн.параметрс заданной надежностью . При этом наз. точностью оценки.

Замечание. Неверно говорить, что попадает в интервал. Задача состоит в том, чтобы построить такой интервал, который бы заключал в себе.

Доверительные интервалы строятся следующим образом:

1) вычисляется точечная оценка ,

2) выбирается надежность ,

3) вычисляется точность оценки .

31.Стандартная ошибка точечной оценки

_{Пусть -точечная оценка параметра .}

_{Стандартная ошибка точечной оценки-наз.среднее квадратич. отклонен.от оценки}

. Посчит.её ошибку:

M(x_i)=a ; D(x_i)=σ²

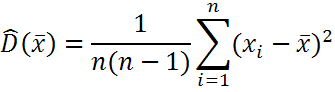
32. Распределение , Стьюдента и Фишера.

Распред.(хи-квадрат).Пусть независимы и имеют станд.норм.распред. Тогда СВназ. распред-ной по з-нусn степенями свободы. МО и дисп.распред.: ,

Г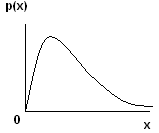рафик – плотность распределения.

При n распред.медленно стрем.к норм.

Распред.Стьюдента.Пусть инезависимы иимеет станд.норм.распр-ние,а-распред.сk степ. свободы. ТогдаСВназ.распред.поз-ну Ст.с k степ.свободы.

При k распред.Ст.быстро стрем. к норм. МО и дисп.распред.Ст.:MT=0, DT=.

Р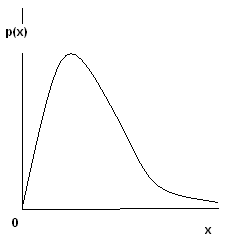аспред.Фишера.Пусть инезависимы и имеют распред.сичислом степ.свободы соотв-нно. Тогда СВназ.распред.поз-ну Фишера cичислом степ.свободы.

Замечание. Табличн.знач.СВФишера всегда >1.

33.Довер.Интервалы для оценки мОпри известном

Пусть изучаемый признак Х имеет норм.распред.и значение параметра известно. Построим по выборке (x₁, x₂,…,x_n) доверительный интервал для оценки а.

Несмещенной и состоятельной оценкой МО-ния явл. выборочная средняя.

Пустьвыбрали,найдем..Довер.интерв.будет иметь вид:

.

Здесь n-объём выборки. Точность оценки

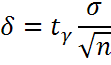
где знач.числа t _γ находится с пом.таблиц функции Лапласа на основании выбранной надежности γ из уравнения 2Ф₀(t_γ)=γ

33. Доверит.Интервалы для оценки мо нормального распределения при неизвестном

Пусть изучаемый признак Х имеет нормальное распределение. Построим по выборке доверительный интервал для оценки математического ожидания.

Несмещенной и состоятельной оценкой матожидания является выборочное среднее значение.

1. Значение параметра неизвестно.

В этом случае довер.интервал будет иметь аналогичный вид, только вместо нужно подставить его оценку:

.

В результате дов.инт.имеет вид

В этом случае определяется по таблице распределения Стьюдента на основаниии числа степеней свободы.

Так как при распределение Стьюдента быстро стремится к нормальному, то при больших объемах выборки () при нахожденииможно пользоваться таблицей функции Лапласа.