6. Смешанное произведение трёх векторов

Пусть даны векторы ине лежащие на одной плоскости. Векторвекторно умножим на вектори полученный результат скалярно умножим на векторполучим числоЭто число называетсявекторно-скалярным или смешанным произведением трех векторов Векторыназываются компланарными, если они лежат в одной плоскости или параллельных плоскостях. Если с заданием трёх векторов указано, какой из них считается первым, какой вторым и какой третьим, то говорят, что заданаупорядоченная тройка векторов. В тексте будем записывать в порядке нумерации. Например, если пишем , то значит- первый вектор,- второй,- третий.

Свойства смешанного произведения

а) смешанное произведение векторов равно объему параллелепипеда, построенного на векторах. Знак произведения будет положительным, если векторыобразуют правую тройку векторов, знак будет отрицательным, если тройка векторов- левая. Легко увидеть, что, поэтому смешанное произведение обозначают символом:.

б) Смешанное произведение векторов равно нулю в том и только в том случае, когда эти векторы компланарны.

7. Смешанное произведение в координатной форме

Пусть заданы векторы , , , тогда

. Смешанное произведение трёх векторов , (а в с)= 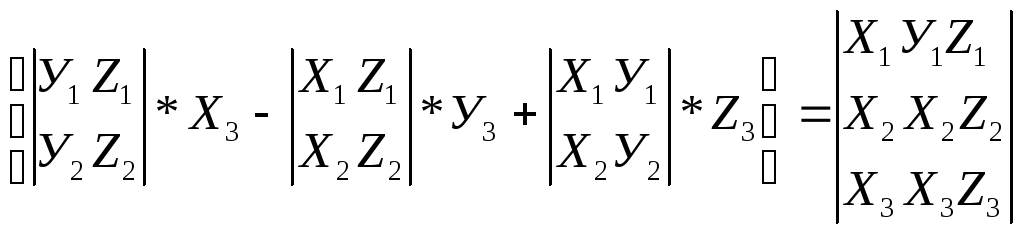(3.27)

Пример: Даны точки А(1;1;1), В(4;4;4), С(3;5;5) и D(2;4;7). Найти объём тетраэдра АВСD.

Решение: Объём тетраэдра V равен одной шестой объёма параллелепипеда V т.е: V=V

Решение: На основании первого свойства V=

Найдём векторы ,,:,

Тогда по формуле (7.1) получим: V= = 18.

Тогда объёма тетраэдра: V=18=3.

8. Уравнение поверхности и уравнение линии в пространстве

Уравнение поверхности

Будем рассматривать поверхность, как геометрическое место точек. Обозначим через х,у,z координаты точек произвольной точки данной поверхности. Следовательно уравнение F(х;у;z)=0, которому удовлетворяют координаты точек поверхности будет уравнением этой поверхности. Уравнения поверхности составляются на основании определения или свойств, присущих этой поверхности.

Пример: Составить уравнение поверхности все точки которой, равноудалены от одной точки О(а;в;с). В декартовых координатах это уравнение имеет вид:

(х-а)+(у-а)+(z-с)=R(3.28)

где R – расстояние от точки О до произвольной точки поверхности. (3.28) – уравнение сферы.

Уравнение плоскости.

Составим уравнение плоскости. Положение плоскости в пространстве будет вполне определено, если зададим на ней некоторую фиксированную точку Ми векторнормальной к плоскости, уравнение которой необходимо составить. Пусть М- произвольная точка, лежащая на плоскости. Составим вектори он перпендикулярен векторуN. Иначе говоря, точка М, лежащая на плоскости характеризуется условием:

В этом случае отсюда имеем:

А ((3.29)

Это есть искомое уравнение плоскости , т.к ему удовлетворяют координаты точек М. Раскрывая (3.29) получим: Ах+Ву+Сz- Ах-Ву-Сz=0 или Ах+Ву+Сz+D=0, где D=- Ах-Ву-Сz (3.30)

Уравнение (3.30) называется общим уравнением плоскости.

В уравнении плоскости переменных х,у,z, входят в первой степени.

Следовательно, в декартовых координатах каждое уравнение первой степени определяет плоскость.

Пример: Составим уравнение плоскости, которая проходит через точку Мперпендикулярно векторуB(1;2;3).

Решение: Согласно уравнению (3.29) искомое уравнение имеет вид:

1(х-1)+2(у-2)+3(2-1)=0 или х+2у+3z-8=0.

Неполные уравнения плоскостей

Рассмотрим некоторые частные случаи уравнения первой степени.

а) Пусть D=0, тогда уравнение плоскости имеет вид Ах+Ву+Сz=0 и определяет плоскость которая проходит через начало координат.

б) Пусть С=0, уравнение плоскости имеет вид Ах+Ву+D=0. Эта плоскость проходит параллельно оси Оz.

в) Пусть В=0, С=0, тогда уравнение плоскости имеет вид Ах+D=0 и определяет плоскость, параллельную координатной плоскости Оуz.

Из последнего уравнения имеем: обозначимтогда получим: х=а

По аналогии с пунктами а), б), в) можем получить: Ах+Сz+D=0 уравнение плоскости параллельной оси Оу; Ву+Сz+D=0 уравнение плоскости параллельной оси Ох;

Уравнение вида Ву+D=0 определяет плоскость, параллельную плоскости Охz. Уравнения Сz+D=0 определяет плоскость параллельную координатной плоскости Оху. Последние два уравнения можно переписать у=в, z=c, где . Уравнения х=0, у=0,z=0 определяют координатные плоскости Оуz, Охz, Оху соответственно.

Уравнение плоскости «в отрезках»

(3.31)

Это есть уравнение плоскости «в отрезках». Числа а, в, с величины отрезков, которые отсекает данная плоскость на координатных осях.

Пример: Составим уравнение плоскости, зная, что она отсекается на осях координат отрезки, а=2, в=-3, с=4.

Решение: На основании (8.4) получим: или 6х-4у+3z-12=0

Нормальное уравнение плоскости

хсоs уcos zcos=р – нормальное уравнение плоскости.

Определим расстояние от точки М(до плоскостихсоs уcos zcos-р(3.32)

Пусть Ах+Ву+Сz+D=0 и хсоs уcos zcos-р=0 определяют одну и ту же плоскость. Тогда коэффициенты этих уравнений должны быть пропорциональны, т.е

coscoscoscos(3.33)

Отсюда: соscoscos

(3.34)

называется нормирующим множителем уравнения (3.32). Для определения знака используем равенство (3.34). Так как, тогда знак нормирующего множителя должен быть противоположен знакуD.

Пример: Даны плоскость 3х-4у+12z+14=0 и точка М(4;3;1). Найти расстояние от точки М до данной плоскости.

Решение: Приведём данные уравнение к нормальному виду. Из формулы (3.34) найдём нормирующий множитель:

Нормальное уравнение имеет вид:

Используем формулу (3.32) и найдём расстояние от точки до плоскости: d=(3*4-4*3+12*1+14)=2

Общее уравнение прямой в пространстве

В пространстве любая линия рассматривается как пересечение двух поверхностей. В частном случае прямая есть линия пересечения двух не параллельных плоскостей. Поэтому общее уравнение прямой в пространстве можно задать двумя уравнения:

(3.35)

Легко убедится, что для не параллельных плоскостей:

Совокупность плоскостей, проходящих через одну и ту же прямую, называется пучком плоскостей.

Уравнения вида (3.36) называется уравнением пучка плоскостей. Задавая различные значенияможно определить все плоскости пучка.

Каноническое уравнение прямой в пространстве

Пусть дана прямая в пространстве. Каждый не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором этой прямой. Обозначим направляющий вектор произвольной прямой буквой , его координаты буквами1, m, n т.е .

Выведем уравнение прямой, проходящей через точку и имеющий направляющий вектор. Пусть произвольная точка прямой. Векторколлинеарен вектору. Следовательно, на основании условия коллинеарности векторов имеем:

(3.37)

Уравнение (3.37) называется каноническим уравнением прямой в пространстве.

Условия параллельности и перпендикулярности двух плоскостей.

Пусть даны плоскости:

Угол между двумя плоскостями равен углу между нормалямик этим плоскостям и определяется по формуле:

(3.38)

Если плоскости перпендикулярны то Отсюда построим условия перпендикулярности:(3.39)

Если плоскости параллельны, то:

или

что равносильно равенству: (3.40)

Условия перпендикулярности и параллельности плоскости и прямой

Пусть даны плоскость Ах+Ву+Сz+D=0, и прямая

Прямая и плоскость параллельны, если направляющий вектор прямой и нормальный вектор к плоскостиперпендикулярны. Отсюда получаем условия параллельности прямой и плоскости:

А1+Вm+Сn=0 (3.41)

Прямая и плоскость перпендикулярны, если направляющий вектор прямой и нормальный вектор плоскости коллинеарны. В этом случае условие перпендикулярности прямой и плоскости имеет вид:

(3.42)

Пример: Составим уравнение плоскости, проходящей через прямую 3х+2у+5z+0, х+4у+3z+4=0, параллельно прямой .

Решение: Составим уравнение пучка плоскостей, проходящих через первую из данных прямых:

3х+2у+5z+6+(х+4у+3z+4)=0

или (3+)х+(2+4)у+(5+3)z+6+4=0 (*)

В этом случае необходимо выбрать плоскость, параллельную второй данной прямой используя условие параллельности (8.14) прямой и плоскости 3(3+)+2(2+4*)-3(5+3)=0

Найдём и подставим в уравнение (*), тогда получим искомое уравнение: 2х+3у+4z+5=0.