3.1. Однородная неограниченная пластина

Для плоской пластины (λ=const), равномерно охлаждаемой с обеих сторон (рис. 6), задана температура поверхности .

Одномерное температурное поле в пластине толщиной 2δ

, (3.1) где 0 ≤ x ≤ δ .

В формуле (3.1) при x=0 температура в середине толщины пластины

. (3.2)

Учитывая зависимость в условиях больших перепадов температур, температурное поле в пластине можно рассчитать по формуле

.(3.3)

Для плоской пластины (λ=const), равномерно охлаждаемой с обеих сторон, заданы температура среды и коэффициент теплоотдачи α . Одномерное температурное поле в пластине

,(3.4) где 0 ≤ x ≤ δ

В формуле (3.4): при x = δ температура на поверхности пластины

(3.5)

при x=0 температура в середине толщины пластины

. (3.6)

Мощность внутренних источников теплоты для пластины определяется по формулам

; (3.7)

;(3.8)

. (3.9)

Связь между объемной и поверхностной плотностями тепло выделения используется при определении теплового потока на боковых поверхностях пластины

;.(3.10)

3.2. Цилиндрический стержень

Для бесконечного стержня (λ=const) задана температура на оси .

Температурное поле в стержне диаметром d₀

,(3.11) где .

В формуле (3.8) при температура на поверхности стержня

,(3.12)

С учетом зависимости температурное поле в стержне

.(3.13)

Для стержня (λ=const), равномерно охлаждаемого средой, заданы ее температура и коэффициент теплоотдачи α . Температурное поле в стержне

.(3.14)

В формуле (3.14):

при температура на оси стержня

;(3.15)

при температура на поверхности стержня

.(3.16)

Мощность внутренних источников теплоты для стержня

;(3.17)

;(3.18)

.(3.19)

Лекция №9

Тема: ТЕПЛООБМЕН С УЧЕТОМ ВНУТРЕННИХ ИСТОЧНИКОВ

ТЕПЛОТЫ

План лекции

3.3. Цилиндрическая труба

3.4. Теплообмен в условиях электрического нагрева

3.3. Цилиндрическая труба

Теплота отводится через внешнюю поверхность трубы. Температур­ное поле в стенке трубы с внутренним радиусом и внешним

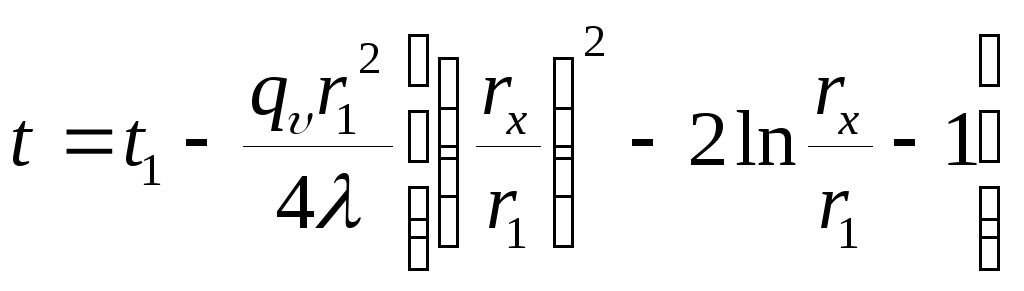,(3.20) где ; — температура на внутренней теплоизолированной по­верхности трубы.

Подставляя в формулу (3.20) можно получить расчетное выражение для перепада температуры в стенке

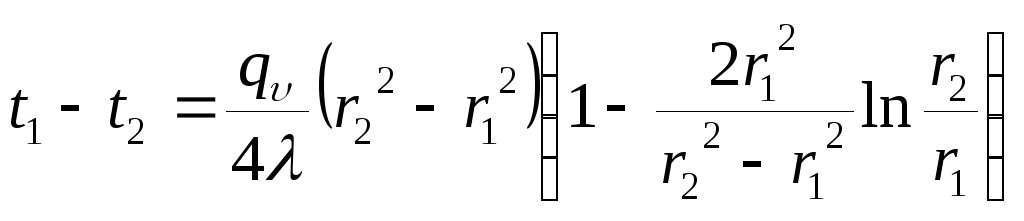(3.21)

и формулу для линейной плотности теплового потока

,(3.22) где t₂ — температура на внешней поверхности трубы.

Теплота отводится через внутреннюю поверхность трубы.

Температурное поле в стенке трубы

.(3.23)

Перепад температур в стенке

.(3.24)

Линейная плотность теплового потока

.(3.25)

Теплота отводится через обе поверхности трубы.

Перепад температур в стенке

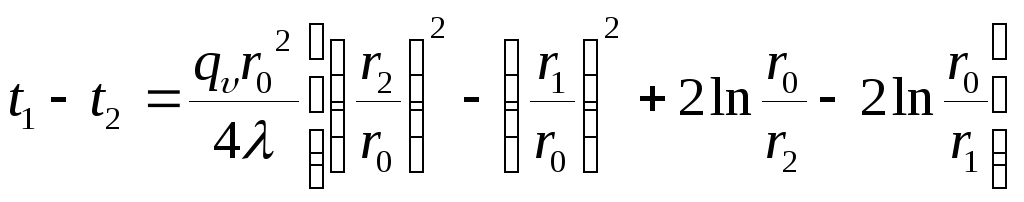,(3.26) где — радиус поверхности, которая имеет наибольшую температуру ,.

Этот радиус определяется из зависимости

.(3.27)

Наибольшую температуру в стенке трубы можно найти по выражению

или (3.28)