
Lektsiyi_7-15
.pdf
Запишемо рівняння M x , Му , Мz для кожної ділянки |
|
||
Ділянка АВ: |
0 ≤ х ≤ а |
|
|
Mx=Mk=0; |
My=0; |
Mz=Fx (нижні); |
|
Mz(0)=0; |
Мz (а)=Fа (нижні). |
. |
|
Ділянка ВС: 0≤ х≤b
Мх =Мк =Fа; Му =0; Мz =Fх (нижні);
Мz(0)=0; Мz(b)= Fb (нижні).
За одержаними значеннями будуємо епюри М к = М х , М у , М z
(рис. 9.1).
Таким чином, на ділянці АВ маємо прямий згин, а на ділянці ВС — згин з крученням. На цій ділянці небезпечний переріз — защемлення С. В цьому перерізі виникає максимальний згинальний і крутний момент.
9.2 Аналіз напруженого стану. Визначення головних напружень
Обмежимося лише розглядом стержнів круглого поперечного перерізу. При сумісному поперечному згині і крученні у поперечному перерізі стержня виникають нормальні напруження від згинального моменту і дотичні напруження, пов'язані з поперечними силами і крутними моментами. Однак, вплив поперечних сил настільки малий, що ними можна знехтувати і брати до уваги лише нормальні напруження згину і дотичні напруження кручення.
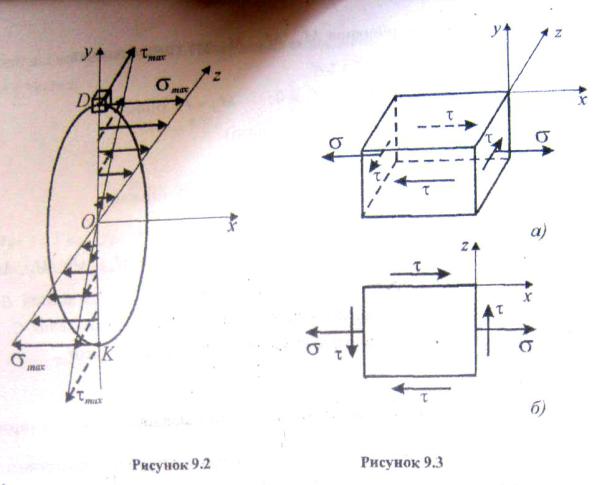
Побудуємо епюри σ і τ в небезпечному перерізі С (защемлення) (рис.9.2). Небезпечними точками у перерізі С є точки D і К, у яких одночасно виникають максимальні нормальні та дотичні напруження. Ці напруження визначаються за формулами
. (9.1)
Виділимо біля точки D нескінченно малий паралелепіпед (рис. 9.2). По чотирьох Його гранях діють дотичні напруження, па двох гранях діють нормальні розтягуючи напруження. Інші грані вільні від напружень (рис. 9.3 а). Отже, ми маємо плоский напружений стан, для якого (рис. 9.3 б)
(9.2)
Головні напруження за формулою (6,8) |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√( |
) |
|
|
|
|
|
|
√ |
|||||||||
|
|
|
|
|
|
||||||||||||||||||
Отже, |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(9.3) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

9.3 Зведений момент. Розрахунок на міцність
Міцність стержня при плоскому напруженому стані треба перевіряти за однією з теорій, залежно від очікуваного характеру руйнування. Якщо передбачається пластичне руйнування, то за третьою теорією міцності
|
|
|
|
|
|
|
[ ]. |
(9.4) |
|
Підставляючи (9.3) в (9.4), маємо |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
[ ]. |
(9.5) |
||||
Підставляючи в (9.5) значення для σ і τ з формули (9.1) і |
|||||||||
враховуючи, що Wp=2Wz , умову міцності можна записати так: |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
√ |
[ ] |
|
|
|||||
|
|
|
|
|
|
|
|
(9.6) |
|
або |
|
||||||||
|
|
|
|||||||
|
|
[ |
], |
|
(9.7) |
||||
|
|
||||||||
де через |
позначений зведений момент, що дорівнює |
|
||
|
√ |
|
|
|
|
. |
(9.8) |
||
Якщо стержень згинається в двох взаємно перпендикулярних площинах хz і ху, то згинальні моменти Му і Мz можна розглядати як складові згинального моменту М і за формулою (8.1)
. (9.9)
Звідси Мз г =Ms =√ |
|
, а |
√ |
(9.10) |
З формули (9.7) випливає формула підбору круглого поперечного перерізу при сумісній дії згину і кручення

|
|
|
|
|
|
|
|
|
√ |
|
|
|
(9.11) |
|||
[ |
] |
[ |
] |
|
||||||||||||
Якщо вести перевірку за |
четвертою |
теорією |
міцності |
|||||||||||||
(енергетичною), то |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
[ ] |
|
|||
|
√ |
|
|
|
|
|
|
|
(9.12) |
|||||||
|
|
|
|
|
|
|
||||||||||
Таким чином |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
√ |
|
|
|
|
(9.13) |
|||||||||
Лекція 10
ЗАГАЛЬНІ МЕТОДИ ВИЗНАЧЕННЯ ПЕРЕМІЩЕНЬ
1О.1 Метод Мора
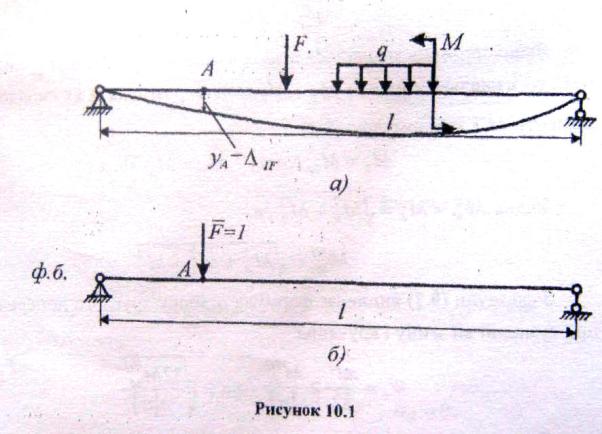
Нехай для балки, що працює на прямий згин при довільному навантаженні системою сил Р (рис. 10.1, а), треба визначити прогин УА = 1 F у довільному перерізі А. Для цього треба вибрати фіктивну балку (ф.б.) (задана балка без силових факторів) і у точці А прикласти фіктивну безрозмірну одиничну силу (рис. 10.1 б).
До цих двох зрівноважених станів навантаження застосуємо принцип можливих переміщень, згідно з яким
A+V=0,

тобто у випадку рівноваги сил сума можливих робіт зовнішніх і внутрішніх сил, прикладених до системи, дорівнює нулеві. Беручи до уваги лише вплив згинальних моментів, одержимо
( ) ̅( )
∫
звідки
∫ |
( ) ̅( ) |
(10.1) |
|
Одержана формула називається інтегралом Мора для визначення переміщень від дії згинальних моментів.
Інтеграл Мора для визначення переміщень з врахуванням поздовжніх сил, згинальних і крутних моментів запишеться у вигляді
∫ ( |
̅ |
|
̅ |
|
̅ |
) |
(10.2) |
|
|
|
|
Коли вирази для внутрішніх сил є різними для різних ділянок стержня, треба обчисляти інтеграли Мора для окремих ділянок і результати підсумовувати.
Для визначення кутових переміщень треба у перерізі, кут повороту якого шукається, прикласти фіктивний одиничний момент ̅ = 1.
10.2 Обчислення інтегралів Мора за способом Верещагіна
Обчислення інтегралів Мора суттєво спрощується, якщо одна з епюр прямолінійна. Така умова завжди виконується для систем, які складаються з прямих стержнів, так як епюри від одиничного навантаження обмежені прямими лініями.
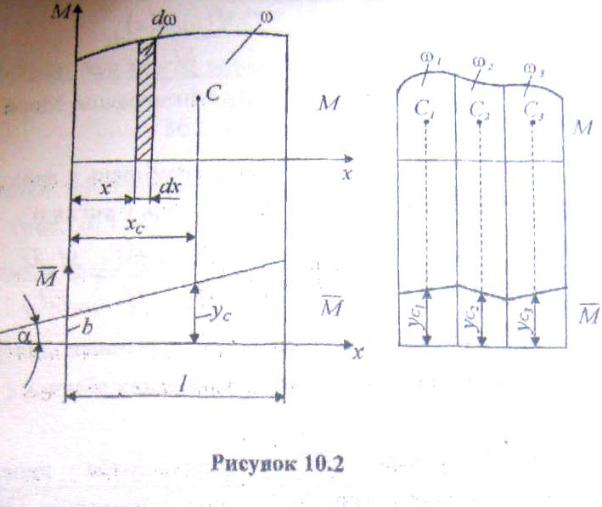
Обчислимо інтеграл Мора ∫ ̅ , для випадку, коли грузова
епюра M від заданого навантаження довільна, а від одиничного навантаження балки зображена прямою, рівняння якої можна записати так
̅ ( ) |
(рис. 10.2) |
Підставляючи цей вираз у формулу інтеграла Мора, одержимо
∫ ( )( |
) |
∫ |
( ) |
∫ ( ) |
(10.2) |
Другий інтеграл в (10.2) являє собою площу грузової епюри
згинальних моментів М і яку позначимо через |
|
∫ ( ) |
(10.3) |
Перший інтеграл в (10.2) — це статичний момент цієї площі відносно осі М, який можна зобразити так:
∫ |
( ) |
(10.4) |
де хс — абсциса центра ваги С епюри М |
|
|
Підставляючи (10.3) і (10.4) в (10.2), одержимо |
|
|
( |
) |
(10.5) |

де ус — ордината з одиничної епюри ̅, яка береться під центром ваги грузової епюри М.
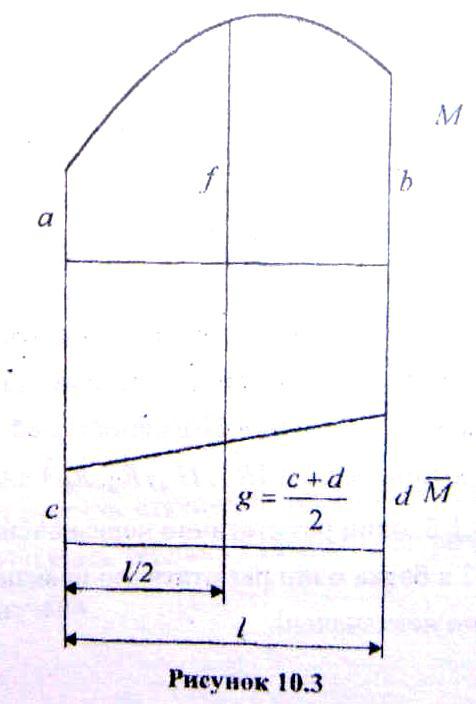
Якщо епюра М — лінія ламана, обчислення інтегралу Мора за формулою (10.5) проводиться по ділянках, на кожній з яких епюра ̅ — прямолінійна (рис. 10.3), Тоді
Підставляючи (10.5) в (10.1), одержимо остаточно формулу Верещагіна для визначення переміщень при дії згинальних моментів
(10.6)
10.3 Обчислення інтеграла Мора за формулою СімпсонаКорноухова
Як відомо з інтегрального числення, якщо проміжок інтегрування l розби-1
ти на дві ділянки, то за формулою Сімпсона
∫ ( ) |
|
( |
) |
(10.7) |
|
Де |
( ) |
( |
|
) |
( ) |
|
Позначимо M(х) ̅(х)=у(х) і використовуючи для обчислення інтеграла Мора формулу Сімпсона (10. 7), одержуємо
∫ ( ) ̅ |
|
|
* |
( |
) ̅( ) |
( |
|
) ̅ ( |
|
) |
( ) ̅( )+ (10.8) |
|||||
|
|
|
||||||||||||||
Якщо позначити (рис. 10.3) |
|
|
|
|
|
|
|
|
|
|
|
|||||
M(0)=a; M( |
|
)=f; M(l)=b; ̅ ( ) |
|
|
̅ ( |
|
)=g; ̅ ( ) |
|
||||||||
|
|
|
||||||||||||||
то (10.8) запишеться у вигляді |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
∫ |
( ) ̅( |
) |
|
|
( |
) |
(10.9) |
|||||||
|
|
|
||||||||||||||
На таку можливість спрощення обчислення інтеграла Мора вперше вказав український вчений Корноухов, тому і формула (10.9) називається формулою Сімпсона-Корноухова.
У загальному випадку функції y(x) формула Сімgсова (10.7) ‘ наближеною. Але якщо підінтегральна функція у(х) с поліномом не вище третього степеня, то формула (10.7) дає точний результат. Отже, якщо М(х) — квадратна парабола, а ̅(х) — лінійна функція, то формула (10.9) є точною.
Формулою (10.9) слід користуватись, коли важко знайти площу або центр ваги грузової епюри М.
