(21)Последовательное соединение звеньев:
Последовательным называется такое соединение звеньев, при котором выходная величина одного звена подается на вход последующего звена.
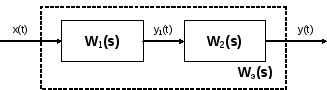
Для этого соединения справедливы следующие соотношения:
Y1(s) = W1(s)·X(s) Y(s) = W2(s)·Y1(s) = W1(s)·W2(s)·X(s) = Wэ(s)·X(s)
Wэ(s) =W1(s)·W2(s)
Для случая последовательного соединения nзвеньев имеем:
Wэ(s) = W1(s)·W2(s)·…·Wn(s)
Другими словами, эквивалентная передаточная функция цепи последовательно соединенных звеньев равна произведению передаточных функций отдельных звеньев.Таким образом цепочку параллельных звеньев в структурной схеме можно заменить одним звеном с передаточной функциейWэ(s) =W1(s)·W2(s)·…·Wn(s).
(22) Параллельное соединение звеньев:
Параллельным называется такое соединение звеньев, при котором на вход всех звеньев подается один и тот же сигнал, а выходные сигналы от всех звеньев суммируются.
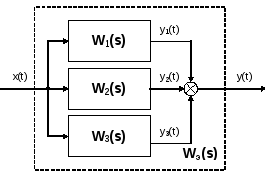
Для этого соединения справедливы следующие соотношения:
Y(s) = Y1(s) + Y2(s) + Y3(s) = W1(s)·X(s) + W2·X(S) + W3(s)·X(s) =
= [W1(s) + W2(s) + W3(s)]·Y(s) = Wэ(s)·X(s)
Wэ(s) =W1(s) +W2(s) +W3(s)
Для случая параллельного соединения nзвеньев имеем:
Wэ(s) = W1(s) + W2(s) +…+ Wn(s)
Другими словами, эквивалентная передаточная функция параллельно соединенных звеньев равна сумме передаточных функций отдельных звеньев.Таким образом цепочку параллельных звеньев в структурной схеме можно заменить одним звеном с передаточной функциейWэ(s) =W1(s) +W2(s) +…+Wn(s).
(23)Соединение звеньев с обратной связью:
Соединение с обратной связью имеет прямую цепь передачисигнала ицепь обратной связи. Обратная связь может быть отрицательной и положительной. При отрицательной обратной связи на вход прямой цепи подается разность межу входным сигналом х(t) и выходным сигналом линии обратной связи. При положительной обратной связи эти величины складываются.
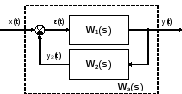
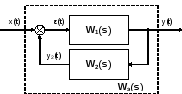
Для соединения с отрицательной обратной связью справедливы следующие соотношения:
Y(s) = W1(s)·E(s) = W1(s)·[X(s) – Y2(s)] Y2(s) = W2(s)·Y(s)
Y(s) = W1(s)·X(s) – W1(s)·Y2(s) = W1(s)·X(s) – W1(s)·W2(s)·Y(s)
Y(s) + W1(s)·W2(s)·Y(s) = Y(s)·[1 + W1(s) ·W2(s)] = W1(s)·X(s)
Y(s) = W1(s)/[1 + W1(s)·W2(s)]·X(s)
В итоге получаем следующее выражение для эквивалентной (результирующей) передаточной функции:
Wэ(s) =W1(s)/[1 +W1(s)·W2(s)]
Для случая соединения с положительной обратной связью получается аналогичное выражение для эквивалентной передаточной функции, только при этом знак плюс в знаменателе изменяется на знак минус:
Wэ(s) =W1(s)/[1 –W1(s)·W2(s)]
Частным случаем соединения с обратной связью является ситуация, когда выходной сигнал от прямой цепи передается без изменения на элемент сравнения или сумматор. Такие обратные связи называются единичными, т.к. у них передаточная функция в обратной цепи равна единице (W2(s) = 1). Тогда эквивалентные передаточные функции для отрицательной и положительной обратной связи упрощаются и принимают следующий вид, соответственно:
Wэ(s) = W1(s)/[1 + W1(s)]
Wэ(s) = W1(s)/[1 – W1(s)]
(24) Правила преобразования структурных схем:
В тех случаях, когда структурная схема оказывается слишком сложной, например, содержит перекрестные связи, ее упрощают пользуясь правилами преобразования структурных схем. Смысл этих правил состоит в переносе элементов структурной схемы из одного положения в другое, так чтобы при этом сохранялась эквивалентность структурных схем.
Перенос узла через звено.
Чтобы перенести узел через звено с передаточной функцией W(s), необходимо включить в линию, не проходящую через звено (выход 2), дополнительный элемент – звено с передаточной функцией 1/W(s). Убедимся, что эти схемы эквивалентны. Действительно, сигнал у(t) после такого переноса не изменится, а сигнал на выходе 2 будет равен: Х(s)·W(s)·1/W(s) = Х(s), т.е. он совпадает с исходным сигналом х(s).
Перенос звена через узел.
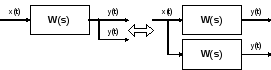
Чтобы перенести звено с передаточной функцией W(s) через узел, необходимо включить в обе линии звенья с передаточной функциейW(s). Легко убедиться, что эквивалентность структурных схем при этом сохраняется.
Перенос сумматора через звено.
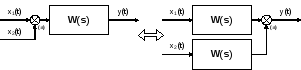
Сразу отметим, что данное правило преобразования структурных схем применимо как к сумматорам, так и к элементам сравнения, т.к. элемент сравнения можно рассматривать как сумматор с инвертированным входом.
Чтобы перенести сумматор через звено с передаточной функцией W(s), необходимо к обоим входам на сумматор добавить дополнительный элемент – звено с передаточной функциейW(s). Убедимся, что эти схемы эквивалентны. Выходной сигнал на исходной схеме равен:Y(s) =W(s)·[X1(s)X2(s)]; выходной сигнал на преобразованной схеме равен:Y(s) =W(s)X1(s)W(s)X2(s), т.е. выходные сигналы совпадают.