1. Передаточная функция.
Передаточная функция апериодического звена I-ого порядка имеет вид:
W(s) = K/(T·s + 1)
где K– коэффициент усиления;T– постоянная времени, характеризующая инерционность системы, т.е. продолжительность переходного процесса в ней. Посколькупостоянная времени характеризует некоторый временной интервал, то ее величина должна быть всегда положительной, т.е. (T> 0).
2. Математическое описание звена.
Апериодическое звено I-ого порядка описывается дифференциальным уравнением первого порядка:
T·dу(t)/dt + у(t) = K·х(t)
3. Физическая реализация звена.
Примерами апериодического звена I-ого порядка могут служить: электрическийRC-фильтр; термоэлектрический преобразователь; резервуар с сжатым газом и т.п.
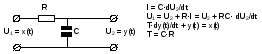
4. Переходная функция.
Переходная функция апериодического звена I-ого порядка имеет вид:
h(t) = L-1[W(s)·1(t)] = L-1[K/(s·(T·s + 1))] = K – K·e-t/T = K·(1 – e-t/T)
Рис. 3.6. Переходная характеристика апериодического звена I-го порядка.
Переходный процесс апериодического звена I-ого порядка имеет экспоненциальный вид. Установившееся значение равно:hуст=K. Касательная в точкеt= 0 пересекает линию установившегося значения в точкеt=T. В момент времениt=Tпереходная функция принимает значение:h(T) ≈ 0.632·K, т.е. за времяTпереходная характеристика набирает только около 63% от установившегося значения.
Определим время регулирования Tудля апериодического звенаI-ого порядка. Как известно из предыдущей лекции, время регулирования – это время, после которого разница между текущим и установившимся значениями не будет превышать некоторой заданной малой величины Δ. (Как правило, Δ задается как 5 % от установившегося значения).
h(Tу) = (1 – Δ)·hуст= (1 – Δ)·K=K·(1 –e-Tу/T), отсюда е-Tу/T= Δ, тогдаTу/T= -ln(Δ), В итоге получаемTу= [-ln(Δ)]·T.
При Δ = 0,05 Tу= -ln(0.05)·T≈ 3·T.
Другими словами, время переходного процесса апериодического звена I-ого порядка приблизительно в 3 раза превышает постоянную времени.
5. Весовая функция.
Весовая функция апериодического звена I-ого порядка имеет вид:
w(t) = L-1[W(s)] = L-1[K/(T·s + 1)] = (K/T)·e-t/T
Рис. 3.7. Весовая функция апериодического звена I-го порядка.
Для весовой функции апериодического звена I-ого порядка характерен скачок в начальный момент времени t = 0. Это происходит из-за того, что на вход звена подается δ-функция. Поскольку δ-функция – это математическая абстракция, которую на практике можно смоделировать в виде короткого импульса, то в реальном, физически реализуемом процессе будет наблюдаться переходный процесс, обозначенный на рисунке пунктиром.
6. Частотные характеристики.
Найдем АФЧХ, АЧХ, ФЧХ и ЛАЧХ апериодического звена I-ого порядка:
W(jω) =K/(T·jω+ 1) =K·(T·jω– 1)/[(T·jω+ 1)·(T·jω– 1)] =
= K·(T·jω– 1)/(-T2ω2– 1) =K/(T2ω2+ 1) – [KTω/(T2ω2+ 1)]·j
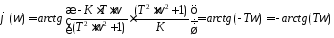
Рис. 3.8. АФЧХ, АЧХ, ФЧХ, ЛАХ и ЛФХ апериодического звена I-ого порядка.
ЛАХ апериодического звена I-ого порядка представляет собой трансцендентную функцию. Чтобы упростить использование ЛАХ, вводят понятиеасимптотических ЛАХ, то есть кусочно-линейных функций, не сильно отличающихся от истинных.
Дифференцирующее звено:
1. Передаточная функция.
Передаточная функция дифференцирующего звена имеет вид:
W(s) =T·s гдеT– постоянная времени (время дифференцирования).
2. Математическое описание звена.
Дифференцирующее звено описывается уравнением, в котором встречается производная от входного сигнала:
у = T·dх(t)/dt
Это не дифференциальное уравнение, поскольку входной сигнал х(t) и его производные полагаются заранее известными.
3. Физическая реализация звена.
Сразу отметим, что идеальное дифференцирующее звено физически нереализуемо. Вообще, любая передаточная функция с порядком числителя большим порядка знаменателя является физически нереализуемой.Укажем, какие факторы могут воспрепятствовать физической реализуемости:
нарушение причинности – выходной сигнал появляется раньше входного;
нереализуемая частотная характеристика, например, не стремящаяся к нулю при бесконечно больших частотах;
появление на выходе бесконечных значений сигналов при подаче физически реализуемых сигналов.
Строго говоря, физически нереализуемой является и ПФ с порядком числителя равным порядку знаменателя.Как мы видели ранее, даже идеальный усилитель не может быть физически реализован, не говоря уже об идеальном дифференцирующем звене, так как в обоих случаях АЧХ не стремятся к нулю при росте частоты.
Поскольку идеальное дифференцирующее звено физически нереализуемо, при этом сама операция дифференцирования часто встречается при описании процессов разной природы, то на практике часто используют "нетиповое" реальное дифференцирующее звено. Реальное дифференцирующее звено являетсясоединением двух типовых звеньев - идеального дифференцирующего и инерционного, которые вместе приближённо описывающих операцию дифференцирования. Передаточная функция реального дифференцирующего звена имеет вид:
W(s) =T1s/(T2s+ 1), гдеT1– постоянная времени дифференцирующей составляющей (время дифференцирования), аT2– постоянная времени апериодической составляющей. При малых значенияхT2, т.е. когда инерционность апериодического звена мала, составляющейT2sв знаменателе передаточной функции можно пренебречь, тогда мы получим приближенную передаточную функцию идеального дифференцирующего звена:
W(s) =T1s/(T2s+ 1) ≈T1s.
Такое звено хорошо работает при низких частотах. Максимальная частота, при которой реальное дифференцирующее звено еще работает "почти как идеальное" равна:
ω = 1/T2.
Примерами дифференцирующего звена являются дифференцирующая цепочка, дифференцирующий трансформатор, операционный усилитель в режиме дифференцирования.
