4.10. Движение заряженных частиц в магнитном поле

Пусть заряженная частица влетает в однородное поле с индукцией .

Рассмотрим наиболее простой случай, когда скорость частицы перпендикулярна вектору магнитной индукции. На частицу будет действовать сила Лоренца, перпендикулярная к направлению ее движения. Так как (α=π/2), то модуль силы Лоренца равен: . В результате траекторией заряженной частицы будет окружность (рис.4.14).

Сила Лоренца сообщает частице нормальное ускорение и играет роль центростремительной силы. Нормальное ускорение определяется выражением:

, (4.51)

где R - радиус окружности.

Запишем второй закон Ньютона для этого случая:

, (4.52)

или

. (4.53)

Для радиуса окружности получим выражение:

. (4.54)

Формулу (4.54)также можно записать в виде:

. (4.54)

Здесь - удельный заряд частицы.

Период обращения частицы по окружности равен:

. (4.55)

Подставляя в (4.55) выражение для радиуса траектории и производя сокращения, получим:

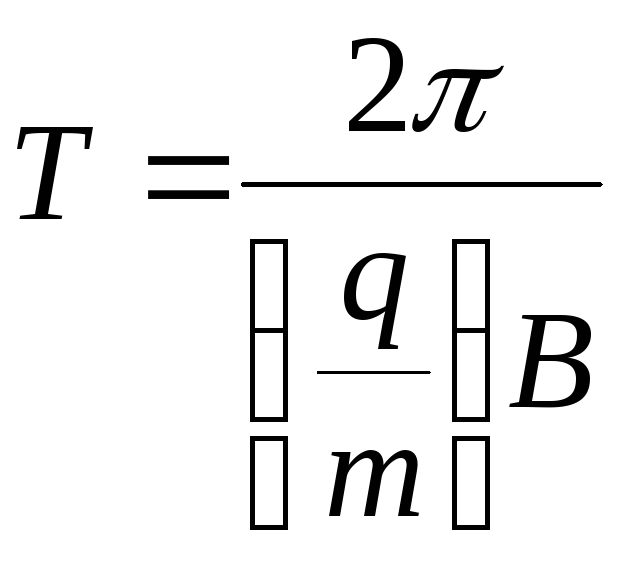. (4.56)

Из выражений (4.54) и (4.56) следует:

• радиус окружности тем меньше, чем больше магнитная индукция;

• период обращения частицы в магнитном поле не зависит от её скорости, а зависит от величины удельного заряда и от магнитной индукции поля.

Изменяется лишь направление скорости, а это означает, что заряженная частица в однородном магнитном поле должна двигаться точно по окружности, если нет составляющей скорости вдоль магнитного поля.

Рассмотрим случай, когда скорость частицы составляет с магнитным полем угол α, отличный от π/2.

Разложим вектор скорости на две составляющие: перпендикулярную магнитному полюи параллельную полю(рис. 4.15). Модули этих составляющих равны:

,

.

Сила Лоренца обусловлена только составляющей и равна (по модулю):

. (4.57)

Заряженная частица будет участвовать в двух движениях:

• в равномерном движении в направлении вектора со скоростью;

• в движении по окружности в плоскости, перпендикулярной направлению вектора , со скоростью.

Врезультате наложения этих двух движений траекторией частицы будет винтовая линия (рис.4.16).

Определим параметры траектории частицы. Радиус винтовой линии будет равен:

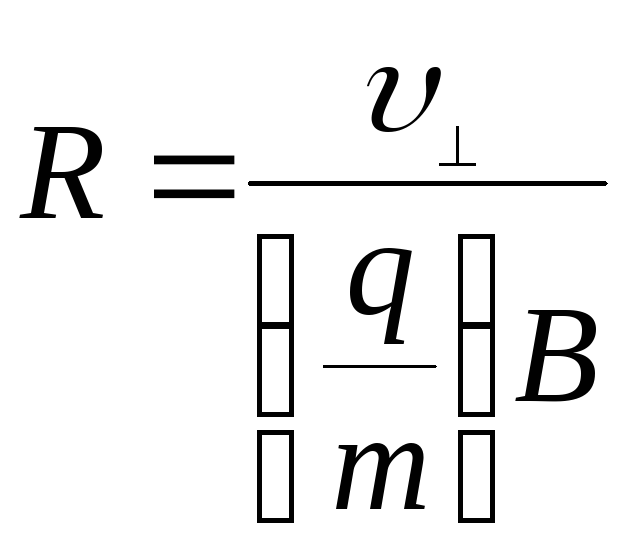=. (4.58)

Шаг винтовой линии

. (4.59)

Рассмотрим случай, когда заряженная частица влетает в неоднородное магнитное поле. Пусть магнитная индукция возрастает в направлении x (рис. 4.17). Тогда заряженная частица будет двигаться по винтовой линии, радиус и шаг которой уменьшаются.

Таким образом,заряженные частицы, влетающие в постоянное магнитное поле, изменяют направление своего движения и навиваются на линии вектора . Этим свойством пользуются в некоторых приборах, чтобы удержать пучки заряженных частиц от расплывания.

Сущность метода магнитной фокусировки (в кратком варианте) состоит в следующем. Если частица движется точно вдоль линии вектора , то магнитное поле не оказывает на нее никакого воздействия. Если частица по каким-то причинам получит составляющую скорости, перпендикулярную к линиям поля, то она все равно не уйдет далеко в сторону от основной траектории и будет двигаться по винтовой линии.