
- •«Тюменский государственный нефтегазовый университет»
- •Физика, часть 2
- •1.Электростатика
- •1.1.Электрические заряды и электрическое поле. Принцип суперпозиций полей
- •1.2.Понятие о плотности заряда
- •1.3.Применение принципа суперпозиции к расчету электростатических полей. Электростатическое поле на оси заряженного кольца
- •Подставим выражение (1.14) в формулу (1.13) и вынесем за знак интеграла постоянные величины, получим:
- •1.4.Геометрическое описание электрического поля. Поток вектора напряжённости
- •1.6.Теорема Остроградского-Гаусса
- •1.7. Применение теоремы Остроградского-Гаусса к расчёту электростатических полей
- •2. Поле двух бесконечных параллельных плоскостей, заряженных разноимённо.
- •3.Поле бесконечного равномерно заряженного по поверхности цилиндра
- •4.Поле равномерно заряженной по поверхности сферы
- •1.8. Работа сил электростатического поля. Потенциал
- •Подставим выражения (1.47) и (1.48) в формулу (1.46), получим:
- •1.9. Циркуляция вектора напряженности электростатического поля
- •1. 10. Связь между напряженностью электростатического поля и потенциалом
- •1.11. Вычисление потенциала по напряженности поля
- •2.Электрическое поле в веществе
- •2.1.Электрическое поле в диэлектриках. Диполь и дипольный момент. Поляризованность
- •Внутреннее электрическое поле в диэлектрике (микрополе) достигает величины Евнутр.1011в/м. Внешние поляЕвнеш..107в/м.
- •Поляризованность диэлектрика определится выражением:
- •Безразмерная величина показывает, во сколько раз напряженность поля в диэлектрике меньше, чем в вакууме. Она называетсяотносительной диэлектрической проницаемостью вещества.
- •2.2.Виды диэлектриков и механизм поляризации
- •2.3. Сегнетоэлектрики и их свойства
- •2.4. Пьезоэлектрический эффект
- •2.5. Вектор электрического смещения. Теорема Гаусса для электрического поля в диэлектрике
- •2.5. Проводники в электрическом поле
- •2.6. Электроемкость уединенного проводника. Конденсаторы.
- •2.6. Параллельное и последовательное соединение конденсаторов
- •2.7. Энергия электрического поля
- •3. Постоянный электрический ток
- •3.1.Характеристики электрического тока
- •3.2.Законы Ома и Джоуля-Ленца для однородного проводника
- •Разность потенциалов на концах цилиндра равна
- •Сопротивление цилиндра выражается формулой
- •3.3.Сторонние силы. Э.Д.С. Закон Ома для неоднородного участка цепи
- •Второй интеграл равен разности потенциаловна концах участка:
- •Это выражение называется законом Ома для неоднородного участка цепи.
- •3.4. Правила Кирхгофа
- •3.5. Классическая электронная теория металлов
- •Вывод закона Ома на основе электронной теории
- •Вывод закона Джоуля-Ленца на основе электронной теории
- •Вывод закона Видемана-Франца на основе электронной теории
- •3.6. Достоинства и затруднения классической электронной теории металлов Классическая электронная теория металлов (как и любая другая теория) имеет свои достоинства и недостатки.
- •3.7. Работа выхода электронов из метала. Термоэлектронная эмиссия
- •4. Магнитное поле в вакууме
- •4.1. Магнитная индукция. Закон Ампера.
- •4.2. Магнитное поле в вакууме. Закон Био-Савара - Лапласа.
- •4.3. Магнитное поле прямолинейного проводника с током
- •4.4. Магнитное поле кругового тока
- •4.5. Магнитный момент витка с током
- •4.6. Магнитное поле движущегося заряда
- •4.7. Вихревой характер магнитного поля. Циркуляция вектора магнитной индукции. Закон полного тока
- •Из рисунка следует, что
- •4.8. Применение закона полного тока. Магнитное поле соленоида и тороида
- •Подставляя (4.43) в (4.42) и производя сокращения, получим: . (4.44)
- •4.9. Сила Лоренца
- •4.10. Движение заряженных частиц в магнитном поле
- •Период обращения частицы по окружности равен:
- •4.11. Эффект Холла
- •4.12. Механическая работа в магнитном поле
- •4.14. Контур с током в однородном магнитном поле
- •4.15. Контур с током в неоднородном магнитном поле
- •5. Магнитное поле в веществе
- •5.1. Намагничивание вещества. Вектор намагниченности
- •5.2. Закон полного тока для магнитного поля в веществе
- •5.3. Магнитные моменты электронов и атомов
- •Движущийся по орбите электрон обладает моментом импульса:
- •5.4. Влияние магнитного поля на орбитальное движение электронов. Объяснение диамагнетизма
- •5.5. Парамагнетизм
- •5.6. Классификация магнетиков
- •5.7. Ферромагнетики и их свойства
- •5.8. Доменная структура и механизм намагничивания ферромагнетиков
- •5.9. Антиферромагнетизм. Ферримагнетизм. Ферриты
- •6. Электромагнитная индукция
- •6.1. Закон электромагнитной индукции. Правило Ленца.
- •6.2. Природа электромагнитной индукции
- •6.3. Токи Фуко
- •. (6.11)
- •6.4. Явление самоиндукции. Э.Д.С. Самоиндукции. Индуктивность
- •6.5. Явление взаимной индукции. Взаимная индуктивность. Трансформаторы
- •6.6. Токи при размыканиии и замыкании цепи
- •Задача об исчезновении тока при размыкании цепи
- •Задача об установлении тока при замыкании цепи
- •6.6. Энергия магнитного поля. Объёмная плотность энергии
1.2.Понятие о плотности заряда
Для упрощения математических расчетов электростатических полей часто пренебрегают дискретной структурой зарядов. Считают, что заряд распределен непрерывно и вводят понятие о плотности заряда.
Рассмотрим различные случаи распределения зарядов.
1.Заряд
распределен вдоль линии.
Пусть на бесконечно малом участке
![]() находится заряд
находится заряд![]() .
Введем величину
.
Введем величину
![]() .
(1.5)
.
(1.5)
Величина
![]() называется линейной плотностью заряда.
Ее физический смысл – заряд, приходящийся
на единицу длины.
называется линейной плотностью заряда.
Ее физический смысл – заряд, приходящийся
на единицу длины.
2.Заряд распределен по поверхности. Введем поверхностную плотность заряда:
![]() .
(1.6)
.
(1.6)
Её физический смысл – заряд, приходящийся на единицу площади.
3.Заряд распределен по объёму. Введем объёмную плотность заряда:
![]() .
(1.7)
.
(1.7)
Её физический смысл – заряд, сосредоточенный в единице объёма.
Заряд, сосредоточенный на бесконечно малом участке линии, поверхности или в бесконечно малом объёме можно считать точечным. Напряжённость поля, создаваемого им, определится формулой:
![]() .
(1.8)
.
(1.8)
Для нахождения напряжённости поля, создаваемого всем заряженным телом, нужно применить принцип суперпозиции полей:
![]() .
(1.9)
.
(1.9)
В этом случае, как правило, задача сводится к вычислению интеграла.
1.3.Применение принципа суперпозиции к расчету электростатических полей. Электростатическое поле на оси заряженного кольца
Постановка задачи. Пусть имеется тонкое кольцо радиуса R, заряженное с линейной плотностью заряда τ. Необходимо рассчитать напряжённость электрического поля в произвольной точке А, расположенной на оси заряженного кольца на расстоянии x от плоскости кольца (рис. ).

Выберем
бесконечно малый элемент длины кольца
dl;
заряд dq,
находящийся на этом элементе равен dq=
τ·dl.
Этот заряд создает в точке А
электрическое поле напряжённостью
![]() .
Модуль вектора напряжённости равен:
.
Модуль вектора напряжённости равен:
![]() .
(1.10)
.
(1.10)
По
принципу суперпозиции полей напряжённость
электрического поля, создаваемого всем
заряженным телом, равна векторной сумме
всех векторов
![]() :
:
![]() .
(1.11)
.
(1.11)
Разложим
вектора
![]() на составляющие: перпендикулярные оси
кольца (
на составляющие: перпендикулярные оси
кольца (![]() )
и параллельные оси кольца (
)
и параллельные оси кольца (![]() ).
).
![]() .
(1.12)
.
(1.12)
Векторная
сумма перпендикулярных составляющих
равна нулю:
![]() ,
тогда
,
тогда![]() .
Заменяя сумму интегралом, получим:
.
Заменяя сумму интегралом, получим:
![]() .
(1.13)
.
(1.13)
Из треугольника (рис.1.2) следует:
![]() =
=![]() .
(1.14)
.
(1.14)
Подставим выражение (1.14) в формулу (1.13) и вынесем за знак интеграла постоянные величины, получим:
![]() .
(1.15)
.
(1.15)
Так
как
![]() ,
то
,
то
![]() .
(1.16)
.
(1.16)
С
учетом того, что
![]() ,
формулу (1.16) можно представить в виде:
,
формулу (1.16) можно представить в виде:
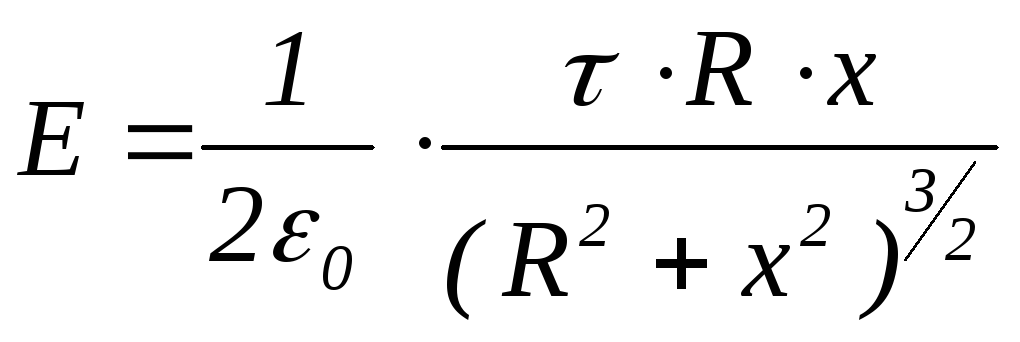 .
(1.17)
.
(1.17)
1.4.Геометрическое описание электрического поля. Поток вектора напряжённости
Для
математического описания электрического
поля нужно указать в каждой точке
величину и направление вектора
![]() ,
то есть задать векторную функцию
,
то есть задать векторную функцию![]() .
.
Существует
наглядный (геометрический) способ
описания поля с помощью линий вектора
![]() (силовых линий) (рис.13.).
(силовых линий) (рис.13.).
Линии напряжённости проводят следующим образом:
касательная к линии в каждой точке должна совпадать с направлением поля;
число линий пересекающих единичную площадку, перпендикулярную к ним, должно быть равно численному значению вектора
 .
.
С
 уществует
правило:
линии вектора напряжённости электрических
полей, создаваемых системой неподвижных
зарядов, могут начинаться или заканчиваться
лишь на зарядах либо уходить в
бесконечность.
уществует
правило:
линии вектора напряжённости электрических
полей, создаваемых системой неподвижных
зарядов, могут начинаться или заканчиваться
лишь на зарядах либо уходить в
бесконечность.
На
рисунке 1.4 показано изображение
электростатического поля точечного
заряда с помощью линий вектора
![]() ,
а на рисунке 1.5 - изображение
электростатического поля диполя.
,
а на рисунке 1.5 - изображение
электростатического поля диполя.
1.5. Поток вектора напряжённости электростатического поля
П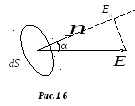 оместим
в электрическое поле бесконечно малую
площадку dS (рис.1,6).
Здесь
оместим
в электрическое поле бесконечно малую
площадку dS (рис.1,6).
Здесь
![]() - единичный вектор нормали к площадке.
Вектор напряжённости электрического
поля
- единичный вектор нормали к площадке.
Вектор напряжённости электрического
поля
![]() образует с нормалью
образует с нормалью
![]() некоторый угол α.
Проекция вектора
некоторый угол α.
Проекция вектора
![]() на направление нормали равна En=E·cos
α .
на направление нормали равна En=E·cos
α .
Потоком вектора
![]() через бесконечно малую площадку
называется скалярное произведение
через бесконечно малую площадку
называется скалярное произведение
![]() ,
(1.18)
,
(1.18)
или
![]() .
(1.19)
.
(1.19)
Поток вектора
напряжённости электрического поля
является алгебраической величиной; его
знак зависит то взаимной ориентации
векторов
![]() и
и
![]() .
.
Поток
вектора
![]() через произвольную поверхностьSконечной величины определится интегралом:
через произвольную поверхностьSконечной величины определится интегралом:
![]() .
(1.20)
.
(1.20)
Е сли
поверхность замкнутая, интеграл отмечают
кружочком:
сли
поверхность замкнутая, интеграл отмечают
кружочком:
![]() .
(1.21)
.
(1.21)
Для замкнутых поверхностей нормаль берется наружу (рис.1.7).
Поток
вектора напряжённости имеет наглядный
геометрический смысл: он численно равен
числу линий вектора
![]() ,
проходящих через поверхностьS.
,
проходящих через поверхностьS.
