Распространение тепла в среде. Уравнение теплопроводности. Решение уравнения теплопроводности для стержня. Моделирование процесса распространения тепла в стержне.

1. Распространение тепла в среде. Вывод уравнения теплопроводности.

Рассмотрим некоторый малый объем среды . Каждая точка этого объема описывается тремя пространственными координатами(рис. 1).

Рисунок 1. Выделенный объем среды

Пусть температура в каждой точке объема описывается функцией (зависит от координат и времени). Каждая точка объема служит источником тепловой энергии. Будем описывать интенсивность (мощность) источников тепла функцией- т.е. каждая точка среды излучает/поглощает тепло с интенсивностью, зависящей от координат и времени.

Чтобы оценить суммарную мощность всех точек объема (иначе – полную тепловую мощность объема) в любой момент времени необходимо взять интеграл от функции по все трем координатам (всему объему):

(здесь - малый элемент объема).

Согласно первому закону термодинамики, изменение энергии системы равно количеству теплоты сообщенной системе (без совершения работы): .

Изменение энергии связано с мощностью соотношением . Отсюда. Тем самым, полное количество тепла, выделившееся в объеме за счет действия источников тепла с суммарной мощностьюза промежуток времениопределиться следующим образом:

(1)

Выделившееся тепло идет на нагрев объема (повышение его температуры) и на теплопередачу (обмен с теплом с внешней по отношению к объему средой).

1.1 Уравнение процесса нагрева

Уравнение для количества теплоты при нагревании/охлаждении каждой точки объема записывается следующим образом:

(2)

где - удельная теплоемкость,- масса- изменение температуры в каждой точке объема.

Данное соотношение необходимо рассмотреть для каждой точки объема, характеризующейся своей удельной теплоемкостью и массой. Примем, что удельная теплоемкость во всех точек одинакова, а вместо массы будем использовать зависимость , где- удельная плотность, также одинаковая для всех точек объема.

Теплота участвующая в процессе нагрева идет на повышение температуры каждой точки объема – т.е. происходит изменение функции :

• в начальный момент времени 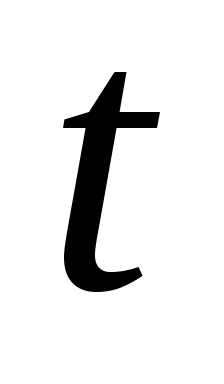температура равна

• через промежуток времени температура станет равной

Приращение температур определится как . Отсюда выражение (2) запишется в следующем виде:

Соответственно для всего объема:

.

Переходя к дифференциальным величинам, предел отношения приращения температур ко времени запишем как частную производную. Отсюдаи окончательно:

(3)

1.2 Уравнение процесса теплопередачи

Теплопередача происходит на границе объема – т.е. сквозь поверхности куба. Уравнение для теплопередачи составляется на основе закона Фурье:

(4)

где - коэффициент теплопроводности,- вектор наискорейшего возрастания температуры,- вектор плотности теплового потока. Знак минус в этом уравнении означает, что направление векторапротивоположно градиенту температуры - т.е. в сторону наибольшего убывания температуры.

Т.к. тепловой поток – это количество теплоты в единицу времени , а плотность теплового потока – это тепловой поток, отнесенный к единице поверхности, то соотношение (4) записанное относительно количества теплоты будет выглядеть следующим образом:

Отсюда полное количество теплоты на теплопередачу, передаваемое через всю поверхность объема определиться как:

(5)