Гармонійний аналіз тимчасового ряду

1. Для визначення вигляду залежності будуємо кореляційне поле тимчасового ряду, тобто наносимо на площину TOY графік функції Y = f(T) (рис. 5.2). Вигляді поля показує, що зі збільшенням T значення Y, в основному, зменшується. Тому за модель залежності може бути прийнята гіперболічна крива

2. Приведемо модель до лінійного вигляду шляхом заміни Z=1/T.

Тоді відповідно до МНК для лінійної залежності Y=a+bZ оцінки параметрів рівняння визначаються за формулами:

; (5.22)

(5,23)

де n - обсяг вибірки (n=12);

- середні арифметичні відповідних значень.

Для розрахунку параметрів знаходимо проміжні значення: вибіркові середні вибіркові дисперсії, середні квадратичні відхилення, парний коефіцієнт кореляції.

У даному випадку одержимо наступні значення:

	50,32	7,09	0,07	0,26	8,8	0,26	2,25	25,32

У результаті гіперболічна залежність набуде вигляду:

+ / T.

3. Перевіримо отриману модель на адекватність статистичним даним. Для цього оцінимо параметр рівняння на значимість відмінності від нуля за критерієм Стьюдента. Розрахункове значення критерію визначимо за формулою:

, (5.24)

де . (5.25)

Дисперсія залишків S²_зал. визначається за формулою:

(5.26 )

Табличне значення знаходимо за таблицею t-розподілу для імовірності =0,05 і числа ступенів свободи k = n-2 = 12-2 = 10.

У даному випадку одержимо наступні значення:

			tb	t кр=t(0,05; 10)

Якщо розрахункове значення критерію Стьюдента більше табличного, то параметр суттєво відрізняється від нуля.

Адекватність моделі визначимо за критерієм Фішера.

Розрахункове значення критерію можна обчислити за формулою:

, (5.27)

де R - коефіцієнт кореляції, обумовлений за формулою:

. (5.28 )

Табличне значення знаходимо за таблицею F-розподілу для імовірності  = 0,05 і числа ступенів свободи k₁ = m = 2 і k₂ = n-m = 12-2 = 10.

У даному випадку одержимо наступні значення:

R2	Fp

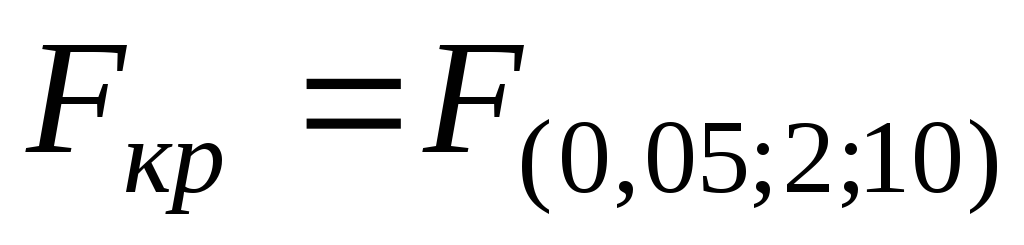
Якщо розрахункове значення критерію Фішера більше табличного, то обрану модель можна вважати адекватною.

4. Для перевірки слушності моделі визначимо наявність автокореляції в залишках із використанням критерію фон Неймана.

Розрахункове значення критерію визначається за формулою:

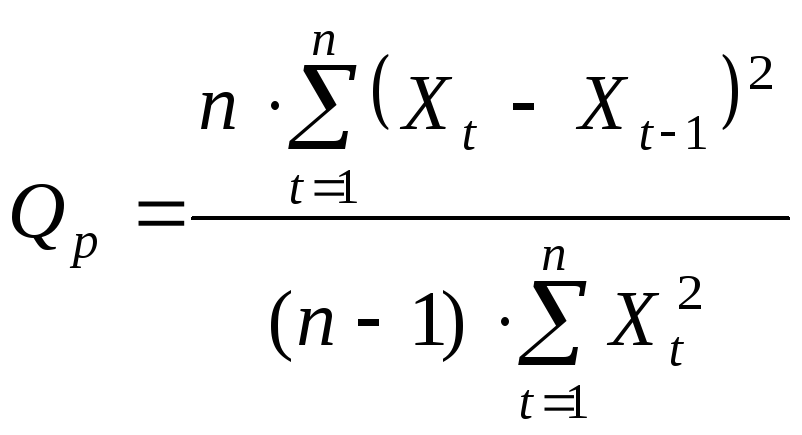, (5.29)

де Хt - значення залишків, тобто .

Для рівня значущості α=0,05 і об'єму вибірки n=12 знаходимо за таблицею критичні значення для критерію фон Неймана Q_L=1,22 і Q_U=3,49.

У нашому випадку, оскільки Q_р < Q_L, то автокореляція залишків є.

Отже, остаточна модель набуде вигляду:

+ / T

і адекватна вихідним даним з імовірністю Р=0,95.

5. Наявність автокореляції залишків говорить про те, що в залишках є невиявлена залежність. Оскільки на графіку, додаток С4, рис.5.3, значні коливання, причому різної амплітуди, то невиявлена залежність періодична. Загальне рівняння має вигляд:

Р₁(t) = А0+А1* cos (Пt/6)+В1 *sin (Пt/6)+А2*cos (Пt/3)+ В2 *sin (Пt/3)

Знаходимо коефіцієнти гармонічних коливань за формулами:

;

; ;

; . (5.30)

Отримуємо:

А0	А1	В1	А2	В2
0
	гармоніка 1		гармоніка 2

6. Для перевірки значущості впливу гармонічних коливань знаходимо квадрати їх амплітуд R₁² та R₂²:

для гармоніки 1 R₁²=A₁²+B₁²; для гармоніки 2 R₂²=A₂²+B₂².

Потім обчислимо розрахункові значення критерію Фішера за формулами:

, (5.31)

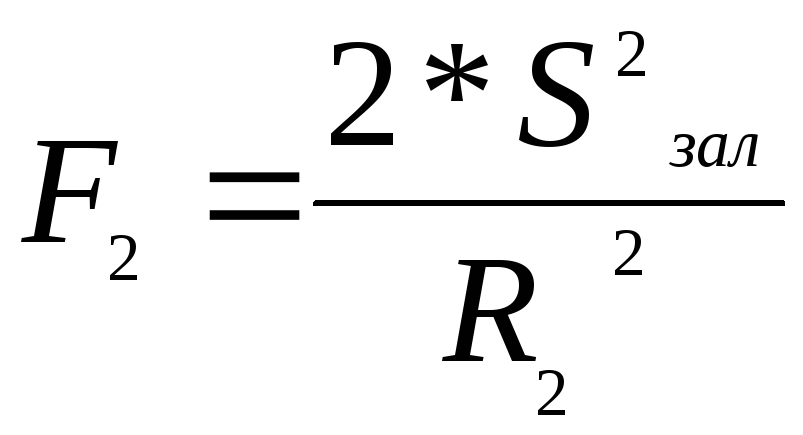. (5.32)

F критичне знаходимо, використовуючи вбудовану статистичну функцію FРАСПОБР(0,05;10;2).

Оскильки F1та F2< F_кр, то вплив гармонік значущий і вони включаються в залежність.

R12	R22	F1=		- значуще
		F2=		- значуще
		Fкр=

Підставляємо розраховані дані у початкове рівняння:

P₁(t)= cos(Pi/6*t)+ sin(Pi/6*t) + cos(Pi/3*t) + sin(Pi/6*t)

та формуємо рівняння тренду с періодичною складовою:

У= + /Т+ cos(Pi/6*t) )+ sin(Pi/6*t) + cos(Pi/3*t) +

+ sin(Pi/6*t)

7. Перевірка адекватності отриманої моделі здійснюється з використанням розрахункового значення критерію Фішера за формулою:

, (5.33)

де залишкова дисперсія знаходиться за формулою

(5.34)

F критичне знаходимо, використовуючи вбудовану статистичну функцію FРАСПОБР(0,05;11;6).

S2зал	Fроз	Fкр
- модель адекватна

Якщо розрахункове значення критерію Фішера більше табличного, то отримана залежність адекватна експериментальним даним.