Практична частина
Завдання: 1. Підприємець хоче покласти на депозит в банк 100 гр.одиниць одноразово під 5% річних на 5 років. Яку суму грошей матиме підприємець наприкінці пятого року?
Завдання 2. Підприємець хоче класти на депозит на трьохрічний строк по 100 гр.од. в кінці кожного року під 5% річних. Яку суму він матиме по закінченні 3 років?
Завдання 3. Скільки часу знадобиться, щоб інвестиція в розмірі 2000 гр.од. зросла до 3000 гр.од. за умови нарахування складних відсотків з 10%-ною ставкою?
1.
Розв'язок:
P = 100 гр. одиниць (початкова сума вкладу)
і = 0,05 (відсоткова ставка)
I = 100 гр. од. х 0, 05 = 5 гр. од. - грошовий вираз відсотка, який отримає підприємець наприкінці 1 року.
n = 1; n = 5.
Таким чином , для n = 1 :
FVn = FV1 = P + I = P + P(i) = P (1+ i) = 100 гр. од. х (1 + 0,05) = 100 гр. од. х (1,05) = 105 гр. од.
Тобто наприкінці першого року підприємець матиме 105 гр. одиниць. Підприємець заробив за перший рік 100 гр. од. х 0,05 = 5 гр. од, тому по закінченні першого року сума внеску дорівнювала вже 100 гр. од + 5 гр. од. = 105 гр. од.
Другий рік почався вже з цієї суми, відсоток склав 5,25 гр. од. Відсоток за другий рік більше відсотку за перший тому, що підприємець заробив вже відсоток на відсоток першого року внеску: 5 гр. од. х 0,05 = 0,25 гр. од. Цей процес продовжується, і внаслідок того, що кожного разу початкова сума вище попередньої, річний відсоток виростає. FV = P х ( 1 + i )n
Таким чином, FV5 = 100 гр. од. х (1,05)5 = 127,63 гр. од.
Відповідь: FV – майбутня вартість вкладу: 127,63 гр. од.
2.
Розв'язок:
Цей приклад відрізняється від попереднього тим, що загальний вклад зроблено не одноразово на певний термін, а серією рівних вкладів, тобто рентою або анюїтетами.
Розрахуємо майбутню вартість анюїтетів або ренти, FVAn.
Здійснюється нарахування платежа на платіж до n-го періоду. Сума цих платежів і є майбутньою вартістю анюїтету, FVАn.
Кожний потік грошових коштів компаундирується для того, щоб отримати FV
FV = Pх(1+ i)0 + Pх (1+ i)1+ Pх (1+ i)2 + . . . + +Pх (1+ i)n-1= Pt=1 х(1+і) n-1 = Pх (1+і)n - 1
Рішення за допомогою таблиць передбачає використання фактору відсотку майбутньої вартості анюїтетів (FVi,n) - фактор відсотку FV для анюїтету за n- періодів з і- процентною ставкою.
Значення FV вже обчислено в таблиці визначення майбутньої вартості анюїтетів. Це стовпчик для 5% для третього періоду FV = 3,1525.
FV = P x (FVi,n).
Таким чином, майбутня вартість ренти в 100 гр. од. буде 100 гр. од х 3,1525 = 315,25 гр. од.
Відповідь: майбутня вартість вкладу: 315,25 гр. од.
3.
Розв'язок:
Оскільки нам відома майбутня і приведена вартість даної інвестиції, застосуємо формулу:
Sn = P0 (ki,n мв), де ki,n мв - коефіцієнт майбутньої вартості при і % n періодів.
ki,n = (1+і) n
ki,n = 3000/2000 = 1,5
Таблиця 3.3
Майбутня вартість 1 гр.Од. При різних термінах внеску і різних процентних ставках
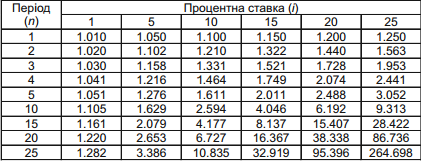
Скористаємося даними табл. 3.3, знайдемо стовпчик, що відповідає 10% і підберемо коефіцієнт майбутньої вартості, найближчий до обчисленого значення - 1,5. Це значення 1,464, дещо менше ніж 1,5 і стосується 4-річного періоду.
Відповідь: Порівнюючи ці показники, дійдемо висновку, що кількість періодів нарахування відсотків в аналізованій ситуації насправді повинна бути дещо більше 4 років.