
- •Предисловие
- •Глава 1. Основные понятия
- •1.1. Логическая символика
- •1.2. Множества
- •1.3. Множество вещественных чисел
- •1.4. Функции
- •1.5. Вопросы для самоконтроля к главе 1
- •Глава 2. Предел функции
- •2.1. Числовая последовательность
- •2.2. Определение предела функции
- •2.5. Замечательные пределы
- •2.6. Разрыв функции. Классификация точек разрыва
- •2.7. Вопросы для самоконтроля к главе 2
- •3.2. Дифференцируемость функции в точке
- •3.3. Дифференцируемость функции на промежутке
- •3.4. Дифференциал функции
- •3.5. Производная суммы, произведения и частного функций
- •3.6. Производные от тригонометрических функций
- •3.7. Дифференцирование логарифмических функций
- •3.10. Производные и дифференциалы высших порядков
- •3.11. Дифференцирование функций, заданных параметрически
- •3.12. Вопросы для самоконтроля к главе 3
- •Заключение
- •Библиографический список
- •Глоссарий
- •Предметный указатель
- •Оглавление
этом точка x может принадлежать или не принадлежать X.
Пример 1.11. 1. Пусть X = (1,4) . Любая точка x , принадлежащая
этому открытому интервалу, принадлежит ему вместе с некоторой своей достаточно малой окрестностью. В силу этого любая точка промежутка (1,4) является его внутренней точкой. Любые окрестности точек x =1 и
x = 4 содержат как точки, принадлежащие промежутку (1,4) , так и точ-
ки, ему не принадлежащие. Следовательно, точки x =1 и x = 4 будут граничными точками промежутка (1,4) , ему не принадлежащими.
2. Пусть X =[0,+∞) . Любая точка x > 0 будет внутренней точкой
этого промежутка. Точка x = 0 будет граничной точкой промежутка X, ему принадлежащей.
Определение 1.16. Множество X R называется открытым, если все его точки внутренние. Примером открытого множества может служить рассмотренный выше интервал (1,4) .
Определение 1.17. Точка x0 R называется предельной точкой для множества X R , если любая ε окрестность точки x0 содержит хотя бы одну точку множества Χ, отличную от точки x0 ; т.е.ε > 0 :Rε (x0 ) ∩(X ‚ {x0}) ≠ . Заметим, что предельные точки могут
быть как внутренними, так и граничными.
Пример 1.12. Пусть X =[0,+∞) . Любая точка x ≥ 0 будет предель-
ной для X по определению, но точка x = 0 при этом является граничной, а остальные - внутренними.
Определение 1.18. Множество X называется замкнутым, если оно содержит все свои предельные точки.
Примерами замкнутых множеств могут служить, например, замкнутые интервалы [a,b].
Приведем без доказательства следующую теорему.
Теорема 1.1. Для того, чтобы множество X R было открытым, необходимо и достаточно, чтобы его дополнение X′ = R ‚ X было замкнутым.
1.4.Функции
1.4.1.Отображения множеств
Определение 1.19. Если даны два непустых множества X и Y. Тогда, если по некоторому закону f , каждому элементу x X ставится в
соответствие один и только один элемент |
y Y , то говорят, что задано |
отображение f множества X в множество Y: |
|
f : X → Y |
(1.1) |
13
Заметим, что в определении не требуется, чтобы каждый элементy Y множества Y был непременно поставлен в соответствие не-
которому y . Не требуется также и чтобы различным элементам из X были сопоставлены различные элементы из Y. Любое y0 , которое полу-
чается при отображении |
f элемента |
x0 X , |
называется образом эле- |
|
мента x0 . Любое x0 , которое при отображении |
f переходит в y0 , назы- |
|||
вается |
прообразом |
элемента |
y0 . |
Пусть X1 X. Тогда |
f (X1 ) ={y Y : y = f (x),x X1} называется образом множества X1 при отображении f .
Пример 1.13. Пусть X - множество студентов x из одной студенческой группы численностью 25 человек. Y - подмножество множества натуральных чисел: Y =1,2,3,4,5. Зададим отображение f следующим
образом: каждому студенту x из множества X сопоставим элемент y из
множества Y, равный оценке, полученной данным студентом на экзамене по математике. Тогда оценка y0 , полученная студентом x0 , будет его
образом при данном отображении f . При этом может оказаться, что для некоторых элементов множества Y (например, для y =1 и y = 5) не
найдется подходящих x , так как не будет студентов, получивших оценки "1" и "5". Некоторые же элементы Y (например y = 3) будут сопо-
ставлены сразу нескольким элементам x из множества X , т.к. именно оценка "3" будет самой распространенной .
1.4.2. Функции. Способы задания
Часто (особенно, если множества X и Y - числовые) вместо термина отображение используют слово функция.
Определение 1.20. Если X R, Y R , то отображение f назы-
вают вещественной функцией одной вещественной переменной или про-
сто функцией.
Заметим также, что для числовой функции принято называть функцией не только закон соответствия между элементами x и y множеств
X и Y, но и саму переменную y , изменяющуюся на множестве f (X) .
Вместо записи (1.1) в этом случае обычно применяется запись вида y = f (x), или, чтобы не вводить лишних букв, пишут y = y(x), где x на-
зывают аргументом функции, y - значением функции. Образ a при отображении f (т.е. f (a) или y(a)) тогда называют значением функции в точке a. Для функции y = f (x) множество X называют областью оп-
ределения функции, а множество f (X) - областью изменения функции
14

или областью значений функции. Очевидно, что f (X) Y. Иногда об-
ласть определения X функции f обозначают через D( f ), а множество значений f (X) , соответственно - E( f ).
Если функция y = f (x) задана с помощью формулы (т.е. аналити-
чески), то под областью определения X понимают множество тех вещественных значений аргумента x , при которых аналитическое выражение f (x) имеет смысл, то есть, выполнимы все указанные в нём действия. В
этом случае множество X принято называть естественной областью определения).
Пример 1.14. Рассмотрим формулу y = 2 − x. Эта формула каждому значению x (−∞,2] ставит в соответствие единственное значение y , причем все эти значения y образуют промежуток [0,+∞). Следова-
тельно, приведенная формула определяет функцию, для которой
X = (−∞,2], f (X) =[0,+∞).
Числовые функции могут задаваться различными формулами на разных промежутках, принадлежащих множеству определения. В этом случае говорят, что функция задана кусочно-аналитически.
Формулы
|
−x, åñëè x [−1,0] |
|
|
y = |
|
|
2x2, åñëè x (0,1] |
|
определяют функцию, для которой X =[−1,1], f (X) =[0,2]. |
||
Иногда функцию, заданную кусочно-аналитически можно задать и |
||
аналитически. Например, |
|
|
2x, åñëè x [0,+∞) |
или y = x+ | x | |
|
y = |
0, åñëè x (−∞,0) |
|
|
|
|
Если множество |
f (X) содержит единственный элемент C (то есть, |
|
всем x X ставится в соответствие одно и то же число C ), то функция называется постоянной. В этом случае пишут f (x) = C или f (x) = const .
Если задано уравнение F (x, y) = 0 , связывающее аргумент x и функцию y , то говорят, что функция задана неявно. В некоторых случаях удается от неявного задания перейти к явному. Например, выражение y = −5/ 1 − x задает функцию y 1 − x + 5 = 0 в явном виде. К сожале-
нию, эта задача не всегда выполнима. Отметим однако, что для решения многих задач переход к явной форме не требуется .
При решении прикладных задач закон соответствия между элементами множеств X и Y, то есть функция y = f (x), часто задается с помо-
15
щью графика, получаемого в результате некоторого эксперимента. Такой способ задания называется графическим.
Если функция задана иначе ( не графически ), то может быть полезно рассмотреть её график.
Определение 1.21. Графиком функции y = f (x) в декартовой пря-
моугольной системе координат Oxy называется множество Γf точек M плоскости Oxy , абсциссы которых являются значениями аргумента x , а ординаты - соответствующими им значениями функции y = f (x).
Γf ={M (x, y) : x X, y = f (x)}.
Множество точек Γf обычно заполняет некоторую линию l . Так что выражение y = f (x), где x X можно рассматривать как уравнение
линии l .
Существует еще один способ задания функции - параметрический. Его часто используют в приложениях. С этим способом мы познакомимся в паpагpафе 1.4.9.
1.4.3. Сложная функция |
|
Рассмотрим две формулы |
|
y = f (u),u U |
(1.2) |
u =ϕ(x),x X. |
(1.3) |
Первая формула определяет функцию y = f (u) |
на множестве U, а |
вторая - функцию u =ϕ(x) на множестве X. Пусть ϕ(X) ∩ U ≠ . Определение 1.22. Функция y = f (ϕ(x)) , аргументом которой яв-
ляется функция ϕ(x) называется сложной функцией переменной x . В
этом случае говорят, что функция (1.2) - внешняя, а функция (1.3) - внутренняя. Сложную функцию называют также суперпозицией (наложением) функций (1.2) и (1.3).
Область определения X сложной функции состоит из тех и только тех значений x X, для которых соответствующие значения u =ϕ(x)
принадлежат множеству определения U функции (1.2). (x X ) (ϕ(x) U).
Переменная u =ϕ(x) называется промежуточным аргументом
сложной функции, тогда как x , принимающая значения из множества
X , аргументом сложной функции в обычном смысле. Можно сказать, что промежуточный аргумент u - это зависимая переменная, а x - независимая.
16
Если ни один элемент множества ϕ(X) значений функции (1.3) не принадлежит множеству U, то есть, если ϕ(X) ∩ U = , то сложная
функция не определена.
Аналогично вводятся сложные функции, являющиеся суперпозицией трех и большего числа функций.
Пример 1.15. 1. Рассмотрим функции y = lg u,u U = (0,+∞),
u =1− x2 ,x X = R,ϕ(X) = (−∞,1].
Множества ϕ(X) и U имеют общие элементы (т.е. их пересечение не является пустым множеством), в силу чего данные формулы определяют сложную функцию на множестве X тех значений x , для которых 1− x2 > 0 . Последнее неравенство эквивалентно следующему: −1 < x <1. Итак, сложная функция y = lg(1− x2 ) определена на множестве
X = (−1,1).
2. Найдём область определения X функции y = arcsin 1+2xx2 . Так как
arcsin u определен только для −1 ≤ u ≤1, то
X ={x :−1 ≤ 1+2xx2 ≤1}.
Преобразуем неравенство 1+2xx2 ≥ −1 к виду (1+2xx)2 ≥ 0 . Множество его решений {−1} (0,+∞). Аналогично получим множество решений (−∞,0) {−1} неравенства 1+2xx2 ≤1. Искомая область определения X есть
пересечение этих множеств, то есть X ={−1;1}. Интересно заметить, что
область определения в данном случае состоит из двух изолированных точек.
1.4.4. Чётные и нечётные функции
Определение 1.23. Функция y = f (x) с областью определения X называется чётной, если x X выполняется равенство f (−x) = f (x) .
Функция y = f (x) с областью определения X называется нечётной, если x X выполняется равенство f (−x) = − f (x).
Функции чётные и нечётные называют функциями общего вида. Из определения следует, что:
1.Область определения чётной и нечётной функций симметрична относительно начала координат.
2.График чётной функции симметричен относительно оси ординат.
17

3. График нечётной функции симметричен относительно начала координат.
Полезно также иметь ввиду следующее: сумма, разность, произведение и частное (знаменатель отличен от нуля) двух чётных функций также чётна; сумма и разность двух нечётных функций нечётна; произведение и частное двух нечётных функций чётно; произведение и частное чётной и нечётной функций нечётно.
Заметим, что сказанное выше предполагает совпадение областей определения обеих функций.
|
Пример 1.16. |
|
1. Функция y = 2x −1 является функцией общего |
|||||||||||
вида, так как её область определения Χ = |
|
1 |
|
|
|
|
|
|||||||
|
|
;∞ не симметрична относи- |
||||||||||||
2 |
||||||||||||||
тельно начала координат. |
|
|
|
|
|
|
||||||||
|
|
|
|
2−x симмет- |
||||||||||
|
2. |
Область определения X = (−2;2) |
функции y = log |
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
2+x |
|
2+x = |
||
рична |
|
относительно |
начала координат. |
|
При этом f (−x) = log |
2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2−x |
||
= log |
2 |
( |
2−x)−1 = −log |
2 |
2−x = − f (x) . Следовательно, данная функция не- |
|||||||||
|
|
2+x |
|
2+x |
|
|
|
|
|
|
|
|||
чётна (см. определение 1.23). |
|
|
|
|
|
|
|
|||||||
|
3. |
Функция |
y = tg2 x + cos x является чётной функцией, так как из |
|||||||||||
чётности y = tg2 x и cos x следует чётность их суммы. |
|
|
|
|
||||||||||
|
|
|
|
|
1.4.5. Периодические функции |
|
|
|
|
|||||
|
Определение 1.24. Функция y = f (x) |
с областью определения X |
||||||||||||
называется периодической, если существует такое T > 0, что:
1)x −T X и x +T X ;
2)x X выполняется равенство f (x) = f (x +T ) ;
3)среди всех таких чисел T есть наименьшее.
Это наименьшее T называется периодом функции y = f (x). Сформулируем свойства периодических функций:
1.Область определения периодической функции симметрична относительно начала координат.
2.Для периодической функции y = f (x) с периодом T на всей об-
ласти определения справедливо равенство f (x + kT ) = f (x) , где k - |
це- |
|||||||
лое число. |
|
|
|
|
|
|
|
|
3. |
Если |
y = f (x) |
периодическая |
функция |
с |
периодом |
T , |
то |
y = f (x + a) также периодическая с периодом T . |
|
|
|
|
||||
4. |
Если |
y = f (x) |
периодическая |
функция |
с |
периодом |
T , |
то |
18

y = f (ax) также периодическая с периодом T / | a |, где a ≠ 0.
Пример |
1.17. |
1. |
Рассмотрим функцию y = 3. Равенство |
f (x) = f (x +T ) |
выполнено |
x R и для всех T > 0, но среди указан- |
|
ных значений T нет наименьшего. Поэтому данная функция не является периодической.
2. Функция y = sin2 x периодическая с периодом π . Действительно,
sin2 x = 1−cos 2x , а функция y = cos x имеет период равный π (см. свой- 2
ство 4).
1.4.6. Ограниченные функции
Определение 1.25. Говорят, что функция y = f (x) с областью определения X ограничена сверху на множестве X0 , ( X0 X ), если существует такое M , что x X0 выполнено неравенство f (x) ≤ M . Функцию y = f (x) называют ограниченной снизу на множестве X0 , если существует такое m, что x X0 выполнено неравенство f (x) ≥ m .
Функцию y = f (x) называют ограниченной на множестве X0 , если существует такое L > 0 , что x X0 выполнено неравенство | f (x) |≤ L.
Если X0 = X, где X - область определения функции y = f (x), то эту
функцию называют ограниченной (соответственно, ограниченной сверху, ограниченной снизу).
Очевидно, что функция ограничена тогда и только тогда, когда она ограничена сверху и ограничена снизу.
Отметим также, что сумма и произведение ограниченных функций также есть ограниченная функция.
Пример 1.18. 1. Рассмотрим функцию y = x2 + 4x +5. Выделяя полный квадрат, получим y = (x + 2)2 +1. Наименьшее значение y =1 эта функция принимает при x = −2. Поэтому множество её значений [1;+∞) .
По определению 1.25 данная функция ограничена снизу.
2. Функция y = sin x + cos x ограничена как сумма ограниченных функций.
1.4.7. Взаимно - однозначные функции. Монотонность
Определение 1.26. Функция y = f (x) с областью определения X и множеством значений f (X) называется взаимно-однозначной, если для
любых |
x1 и x2 , принадлежащих области определения X из условия |
x1 ≠ x2 |
следует, что f (x1 ) ≠ f (x2 ). |
19
Иначе говоря, на всей области определения различным значениям аргумента должны соответствовать различные значения функции.
Можно говорить о взаимной однозначности функции y = f (x) на
некотором подмножестве области определения (в частности, на промежутке).
Пример 1.19. 1. Функция y = x4 −3 не является взаимно - однозначной в области определения X = R , так как f (−x) = f (x) , но она взаимнооднозначна на промежутках (−∞,0], [0,+∞) .
2. Функция y = 2cos x не взаимно - однозначна в области определения X = (−∞,+∞) (например, в силу периодичности), но обладает этим свойством на любом из промежутков [kπ,π + kπ) , где k - произвольное
целое число.
Как легко заметить, достаточным условием взаимной - однозначности функции на некотором подмножестве области определения (промежутке) будет строгая монотонность данной функции на нем.
Напомним соответствующие определения.
Определение 1.27. Функция y = f (x) называется возрастающей на некотором множестве X , если для любых x1,x2 X выполняется соотношение (x2 > x1 ) ( f (x2 ) > f (x1 )), означающее, что большему значе-
нию аргумента отвечает и большее значение функции.
Функция y = f (x) называется убывающей на X, если для любых
x1,x2 X верна импликация: (x2 > x1 ) ( f (x2 ) < f (x1 )), то есть, если большему значению аргумента соответствует меньшее значение функции.
Если функция y = f (x) |
возрастает на X, или убывает на X, |
то она |
|
называется строго монотонной на X. |
|
|
|
Функция называется |
неубывающей на |
множестве X, |
если |
(x2 > x1 ) ( f (x2 ) ≥ f (x1 )) для любых x1,x2 X, |
и невозрастающей на |
||
множестве X, если (x2 > x1 ) ( f (x2 ) ≤ f (x1 )) для любых x1,x2 X. Возрастающие, убывающие, неубывающие и невозрастающие на X
функции называются функциями, монотонными на X.
Заметим следующее: если функция y = f (x) монотонна на X, то
она монотонна на любом подмножестве множества X. При этом характер монотонности сохраняется.
Пример |
1.20. |
Функция |
|
y = x2 возрастает на промежутке |
|
X =[0,+∞) . Множество натуральных чисел N [0,+∞) . Следовательно, |
|||||
если n |
> n , то (n )2 |
> (n )2 для n ,n N . |
|||
2 |
1 |
2 |
1 |
1 |
2 |
20

Отметим следующие важные свойства монотонных функций:
1. Сумма двух возрастающих (убывающих) функций есть возрастающая (убывающая) функция.
2. Если функция y = f (x) возрастающая (убывающая), то функция y = − f (x) убывающая ( возрастающая) функция.
3. Если функция y = f (x) возрастающая (убывающая), то функция y = f 1(x) убывающая (возрастающая) функция.
4.Суперпозиция (см. пункт 1.4.3) двух монотонно возрастающих (убывающих) функций есть монотонно возрастающая функция.
5.Суперпозиция двух функций, одна из которых монотонно убывает,
адругая монотонно возрастает, есть монотонно убывающая функция.
Пример 1.21. Функция y = |
x2x−1 |
убывает на X = (−∞,0) (0,+∞) |
|||
как сумма двух убывающих функций. |
Действительно, y = |
1−x2 |
1 |
− x |
|
x |
= x |
||||
(см. выше свойства 1-3).
1.4.8. Обратная функция
Пусть дана функция y = f (x), для которой X - область определения, Y0 = f (X ) - множество значений. Пусть эта функция взаимно - однозначна на множестве X. Тогда каждому y Y0 будет соответствовать одно-единственное значение x X, такое что f (x) = y .
Определение 1.28. Функция x =ϕ( y) , определённая на множестве Y0 и ставящая в соответствие каждому y Y0 то единственное значение x X, для которого f (x) = y , называется обратной к функции y = f (x). В этом случае функцию y = f (x) называют прямой функцией по отно-
шению к своей обратной.
Соответственно, для функции x =ϕ( y) областью определения будет Y0 , а множеством значений - X.
Если прямая функция y = f (x) задана аналитически, то выражение для обратной функции x =ϕ( y) (при условии, что она существует) получается в результате разрешения уравнения y = f (x) относительно x .
Интересно отметить, что, так как у прямой и обратной функций область определения и множество значений меняются местами, то обратную функцию можно использовать для нахождения множества значений прямой.
Пример 1.22. Найдем множество значений функции y = xx−+12 . Для
21
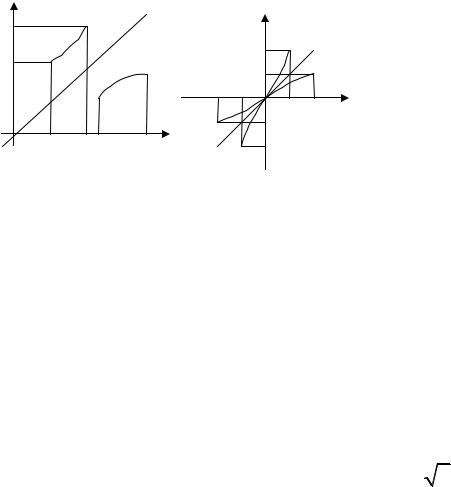
|
этого |
выразим x через |
y : |
x = |
2 y+1 |
. |
Получили обратную |
функцию |
|||||||||||||
|
|
||||||||||||||||||||
|
x =ϕ( y) , |
|
|
|
|
|
|
|
|
|
y−1 |
|
|
|
|
|
|
|
|
||
|
область определения |
которой y ≠1 совпадает с множеством |
|||||||||||||||||||
|
значений |
исходной |
|
функции. |
Итак, |
нашли |
множество |
значений: |
|||||||||||||
|
Y0 = (−∞,1) (1,+∞) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Вводя обычные обозначения для значений аргумента и функции, |
||||||||||||||||||||
y |
y = f (x) |
|
|
|
y |
y |
= arcsin x |
|
будем |
далее |
обратную |
||||||||||
|
|
|
|
функцию записывать в виде |
|||||||||||||||||
β |
|
|
|
|
|||||||||||||||||
x |
=ϕ(y) |
|
|
|
π |
|
= sin y |
|
y =ϕ(x) . |
|
|
|
|||||||||
|
|
|
|
x |
|
|
|
|
|||||||||||||
α |
|
|
|
|
π |
|
2 |
|
|
y |
= sin x |
|
|
|
Из |
школьного |
курса |
||||
|
|
|
− |
|
1 |
|
|
|
= arcsin y |
|
|
||||||||||
|
|
|
|
2 |
−1 |
|
|
x |
известно, что графики пря- |
||||||||||||
|
|
|
|
|
|
1 |
|
π |
x |
|
|||||||||||
O |
|
|
x |
|
|
|
|
|
|
|
|
|
мой |
и |
обратной |
функций |
|||||
|
|
|
|
− |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
α |
β |
α |
β |
|
|
|
−π |
|
|
|
|
|
y = f (x) |
и |
y =ϕ(x) |
сим- |
||||
|
|
|
|
Рис.1.8 |
|
2 |
|
|
|
|
|
метричны |
относительно |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
биссектрисы |
первого и |
||||||||
|
третьего квадрантов (см. рис.1.8). |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Если функция y = f (x) |
не является взаимно-однозначной в области |
|||||||||||||||||||
|
определения X, то существуют такие значения |
x1,x2 X для которых |
|||||||||||||||||||
|
f (x1 ) = f (x2 ) . В этом случае обратной функции не существует. Но ино- |
||||||||||||||||||||
|
гда удается выделить такое подмножество X0 |
X на котором исходная |
|||||||||||||||||||
|
функция взаимно-однозначна (что обеспечивается строгой монотонно- |
||||||||||||||||||||
|
стью). Тогда, если рассмотреть функцию y = f (x), где x X0 , то можно |
||||||||||||||||||||
|
построить функцию y =ϕ(x) , обратную к ней. |
|
|
|
|
|
|
||||||||||||||
|
Пример 1.23. 1. Функция y = x3 (X = R, |
Y = R) возрастает на X. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
Поэтому она имеет обратную функцию y = 3 |
x с областью определения |
|||||||||||||||||||
|
и множеством значений равным R . |
|
|
|
|
|
|
|
|
||||||||||||
|
2. Функция y = sin x, |
ãäå |
X = R, |
|
Y0 =[−1,1] |
не возрастает и не |
|||||||||||||||
|
убывает на X, а поэтому обратной функции не имеет. Однако на интер- |
||||||||||||||||||||
|
вале |
[−π2 ,π2 ] |
она возрастает и принимает все значения из промежутка |
||||||||||||||||||
|
[−1,1]. Поэтому функция y = sin x, |
x [−π2 ,π2 ], имеет обратную функцию |
|||||||||||||||||||
|
y = arcsin x , |
с областью |
определения |
[−1,1] |
и |
множеством |
значений |
||||||||||||||
[−π2 ,π2 ].
1.4.9. Параметрическое задание функции
Введение понятий сложной и обратной функций позволяет рассмотреть еще один способ задания функции, который часто используют в прикладных задачах. Итак, пусть две функции
22
x =ϕ(t), y =ψ (t) |
(1.4) |
аргумента t заданы на некотором промежутке T . Предположим, что x =ϕ(t) взаимно-однозначна на T . Тогда для неё существует обратная
функция t = g(x) (см.п. 1.4.8), подставив которую во вторую из формул (1.4), получим
y =ψ (g(x)) = f (x). |
(1.5) |
Таким образом, в результате исключения t |
из двух равенств (1.4), |
мы пришли к формуле (1.5), определяющей y как функцию от x . Следовательно, задание двух равенств (1.4) равносильно заданию функции y
аргумента x . То есть, эти равенства каждому значению t T ставят в соответствие пару чисел x и y . Первое из них - аргумент функции, а вто-
рое - ее значение
Определение 1.29. Задание функции y = f (x) при помощи ра-
венств (1.4) называется параметрическим способом задания этой функции. Независимая переменная t при этом называется параметром.
Если графиком функции y = f (x) в декартовой прямоугольной системе координат Oxy служит некоторая линия l , то равенства (1.4) назы-
ваются параметрическими уравнениями этой линии.
Тогда равенства (1.4), выражают координаты (x, y) произвольной
точки линии l как функции вспомогательной независимой переменной t (параметра). В то время как параметр t пробегает промежуток T , точка (x, y) вычерчивает линию l на плоскости XOY.
Пример 1. 24. Рассмотрим параметрические уравнения
x = a cost, y = bsin t, t [0,π]. |
(1.6) |
Функция x = a cost убывает на промежутке [0,π] и, следовательно,
она взаимно - однозначна на нем. Поэтому равенства (1.6) определяют функцию y = f (x) с областью определения X = a cos(T ) =[−a,a] и обла-
стью значений Y = bsin(T) =[0,b]. |
Исключим из данных формул пара- |
||||||||
метр t . |
|
|
|
|
x2 |
|
y2 |
|
|
|
x |
= cost, |
y |
= sin t, |
о ткуда |
+ |
=1. |
||
|
a |
b |
a2 |
b2 |
|||||
|
|
|
|
|
|
||||
Таким образом, уравнения (1.6) являются параметрическими уравнениями верхней части эллипса.
Если предположить, что t [π,2π], то получим уравнения нижней части эллипса. Соответственно для t [0,2π] уравнения (1.6) будут в си-
лу 2π - периодичности синуса и косинуса задавать замкнутую кривую: эллипс.
23

Заметим, что выбор параметра t при задании функции y = f (x) в
параметрической форме неоднозначен. Поэтому одна и та же функция может быть записана различными параметрическими уравнениями.
1.4.10. Элементарные функции
Напомним, что собой представляют алгебраические функции. известно, что к алгебраическим действиям относятся: сложение, вычитание, умножение, деление и возведение в степень с рациональным показателем.
Явными алгебраическими функциями называются функции, значе-
ния которых получаются в результате конечного числа алгебраических действий над аргументом и различными постоянными. Существуют три типа таких функций:
1) целая рациональная функция (алгебраический многочлен), т.е. функция вида
y = a0 xn + a, xn−1 +... + an−1x + an ,
где ak R , n 0 N ;
2)дробная рациональная функция – частное от деления двух целых рациональных функций;
3)иррациональная функция – алгебраическая функция, для получения значения которой нужно проделать и действие извлечения из корня.
Например: y = x − 2 , y = x2 + 23 x , y = 1−xx .
Всякая явная функция, не являющаяся алгебраической, называется
трансцендентной функцией. Перечислим так называемые простейшие
трансцендентные функции:
1)Степенная функция y = xa , где a - иррациональное число и x > 0.
2)Показательная функция y = ax (a > 0, a ≠1);
3)Логарифмическая функция y = loga x(a > 0, a ≠1);
4) Тригонометрические функции y = sin x , y = cos x , y = tgx , y = ctgx и др.;
5)Обратные тригонометрические функции y = arcsin x, y = arccos x и др.
Вкурсе математического анализа нам будут встречаться в основном элементарные функции. К ним относятся все алгебраические функции, элементарные трансцендентные функции, а затем все функции, полученные из них с помощью четырех арифметических действий и операции взятия функции от функции, примененных последовательно конечное число раз. Элементарная функция всегда может быть задана анали-
24
