1.2. Двойственная задача

Изучаемые вопросы:

• Правило построения двойственной задачи;

• Двойственная задача распределения ресурсов;

• Экономический смысл двойственной задачи распределения ресурсов.

Каждой задаче линейного программирования соответствует двойственная задача линейного программирования. Исходная задача называется прямой. Сформулируем правило построения двойственной задачи.

Пусть прямая задача записана в канонической форме: найти переменные x₁,x₂,…,x_n, которые максимизируют функциюZ

при ограничениях:

i = 1, 2,…,m, (1.1.8)

j = 1, 2,…,n. (1.1.3)

Тогда по определению двойственная ей задача записывается в виде:

• найти переменные y₁, y₂,…,y_m, которые минимизируют функцию W

(1.2.1)

• при ограничениях:

j=1, 2,…,n(1.2.2)

переменные i = 1, 2,…, m не имеют ограничения знака.

Переменные i = 1, 2,…,mназываютсядвойственными или теневыми ценами. План двойственной задачиY = {y₁,y₂, ….,y_m} называетсядопус-тимым, если все ограничения двойственной задачи (1.2.2) выполняются.

Заметим, что:

• число переменных в двойственной задаче равно числу ограничений в прямой задаче;

• каждому ограничению в прямой задаче соответствует своя двойственная переменная;

• коэффициенты целевой функции двойственной задачи равны правым частям ограничений прямой задачи;

• каждой переменной в прямой задаче соответствует ограничение в двойственной задаче. При этом в левую часть данных ограничений входят коэффициенты перед этой переменной в прямой задаче, умноженные на соответствующие двойственные переменные, а правая часть равна коэффициенту целевой функции прямой задачи перед этой переменной.

Замечание. Если прямая задача на минимум целевой функции, то двойственная задача на максимум и в ее ограничениях (1.2.2) знакнужно заменить на знак:

• найти переменные y₁, y₂,…,y_m, которые максимизируют функцию W:

(1.2.3)

• при ограничениях

j= 1, 2,…,n(1.2.4)

переменные i = 1, 2,…, m не имеют ограничения знака.

Для построения двойственной задачи необходимо привести прямую задачу к каноническому виду и затем записать двойственную ей задачу.

Для задачи распределения ресурсов двойственная задача состоит в определе-нии значений переменных i = 1, 2,…, m, которые минимизируют функцию

(1.2.1)

при ограничениях:

: j = 1, 2,…,n(1.2.2)

: i = 1, 2,…m. (1.2.5)

Ограничение (1.2.5) следует из того, что в (1.1.9) переменная s_i входит только в одно ограничение.

Выясним экономический смысл двойственной задачи распределения ресурсов. Заметим, что каждое слагаемое в левой части ограничений (1.2.2) должно измеряться в тех же единицах, что правая часть, т.е. денежных единицах. Так как коэффициенты a_ij означают удельные нормы затрат ресурсов, то каждаядвойственная переменнаяi = 1, 2,…,mопределяетстоимость единицы ресурса i. Отсюда следует, чтоцелевая функцияв двойственной задаче

определяет стоимость запасов всех ресурсов.

Коэффициенты перед двойственными переменными в левой части двойственных ограничений (1.2.2)

: j = 1, 2,…,n

задают нормы затрат всех ресурсов, необходимых для производства единицы продукции j . Следовательно, левая часть этих ограничений

(1.2.6)

определяет стоимость ресурсов в теневых ценах, затраченных на производство единицы продукции j (удельные затраты на продукцию j).

Обозначим через разность между удельными затратамиz_jи рыночной ценой на продукциюj:

. (1.2.7)

Величину называютприведенной стоимостью (приведенными издержками) производства продукции j.

Производство продукции jназовем:

• убыточным, если выполняется неравенство;

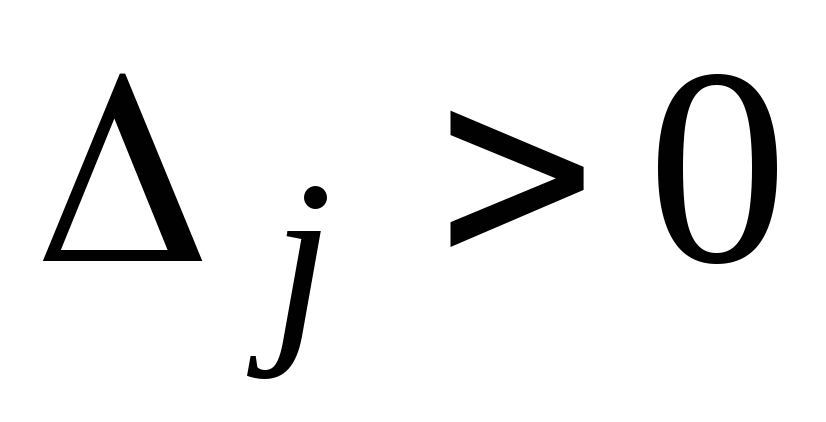• рентабельным, если выполняется равенство;

• прибыльным, если выполняется неравенство.

В этих обозначениях ограничения двойственной задачи (1.2.2)

:j = 1, 2,…,n

можно теперь записать Δ _j ≥ 0.

Отсюда следует, что на допустимых теневых ценах производство всех продуктов неприбыльно.

Тогда двойственную задачу можно записать в виде:

• найти переменные y₁, y₂,…, y_m, которые минимизируют функцию (1.2.1)

• при ограничениях

x_j:Δ_j≥ 0,j = 1, 2,…,n(1.2.8)

: ,i = 1, 2,…,m. (1.2.5)

Можно дать следующую экономическую интерпретацию двойственной задачи. Некоторая фирма предлагает производителю продукции продать ей все запасы ресурсов по теневым ценам y₁,y₂, …,y_m. Неравенства (1.2.2) означают, что в предлагаемых теневых ценах производство всех видов продукции неприбыльно. При этом (1.2.1) означает, что стоимость приобретаемых ресурсов должна быть минимальна. Таким образом, решение двойственной задачи определяет минимальный уровень теневых ценy₁,y₂, …,y_m, при котором производить продукцию неприбыльно.