Пример 3.2.1

Допустим, что матрица выигрышей игрока Iимеет вид:

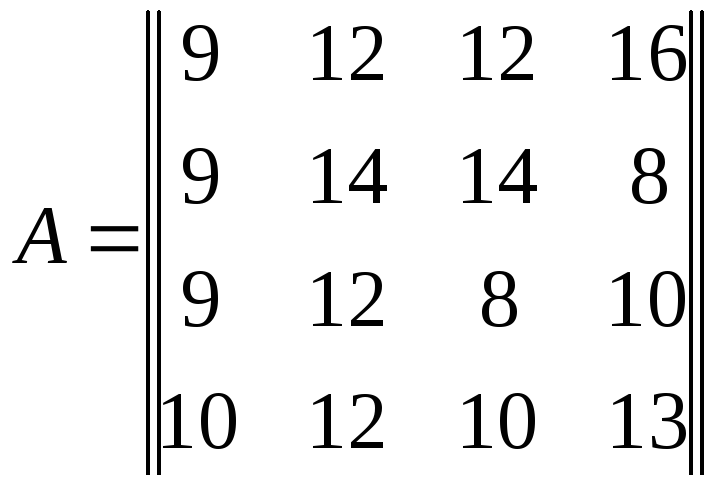
Найдем минимальные элементы в каждой строке и максимальные элементы в каждом столбце

min в строке

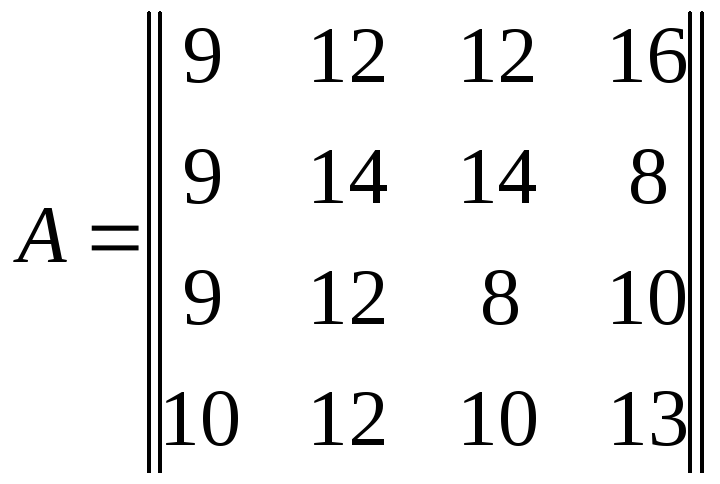
max в столбце

Отсюда следует, что максимальное среди минимальных в строке равно

maxmin{9,8,8,10}=10

и минимальное среди максимальных в столбце равно

minmax{10,14,14,16} =10.

Следовательно, для этой матричной игры выполняется равенство

max min {9,8,8,10}= min max{10,14,14,16} =10,

т.е. значение игры v(A) = 10. В матрице выигрышей три элемента равны 10. Из них только элемент в четвертой строке в первом столбце a(4,1) будет минимальным в строке и максимальным в столбце. Отсюда следует, что оптимальной стратегией игрока I является выбор четвертой строки, а оптимальной стратегией игрока II является выбор первого столбца. Заметим, что выбор игроком I четвертой строки гарантирует ему выигрыш 10. Аналогично выбор игроком II первого столбца гарантирует ему выигрыш 10.

Замечание.Изменение матрицы выигрышей может нарушить ситуацию равновесия в игре. Допустим, что в матрице выигрышей предыдущего примера элементa₄₃ = 10 равен 9

min в строке

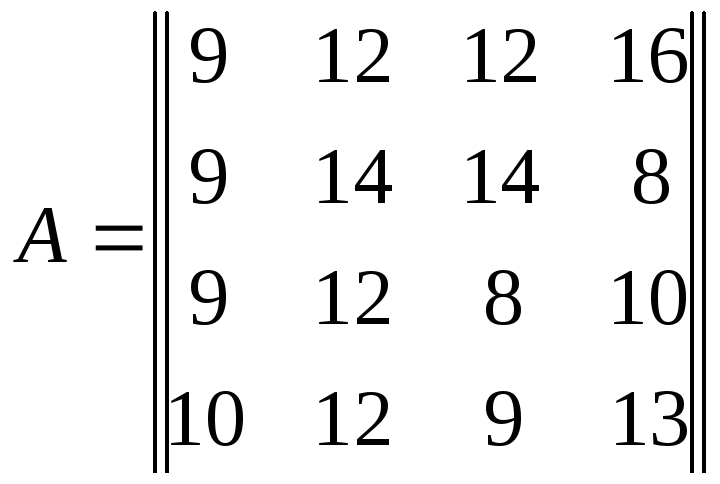
max в столбце

Тогда максимальное среди минимальных в строке равно

maxmin{9,8,8,9} =9, а минимальное среди максимальных в столбце равно

minmax{10,14,14,16} =10.

Для этой матричной игры maxmin{9,8,8,9}≠minmax{10,14,14,16} =10 и, следовательно, решение игры в чистых стратегиях не существует.

Вопросы для самопроверки

1. Какие игры называются антагонистическими?

2. Чему равен выигрыш игрока IIв матричной игре, если выигрыш игрокаIравен 5?

3. Как определяются чистые стратегии игроков в матричной игре?

4. Дать определение ситуации равновесия в чистых стратегиях?

5. Всегда существует ситуация равновесия в чистых стратегиях?

3.3. Решение матричных игр в смешанных стратегиях

Изучаемые вопросы:

• Определение смешанных стратегий;

• Ситуация равновесия в смешанных стратегиях.

Рассмотрим расширение множества стратегий игроков до смешанных стратегий, которое позволяет решить любую матричную игру.

Смешанной стратегией игрока Iназывается любой упорядоченный набор изnчиселp= (p₁,p₂,…,p_n) удовлетворяющий условиям

p₁+p₂ +…+p_n = 1,p_i≥ 0.

Число p_iопределяет вероятность, с которой игрокI выбирает строкуiматрицы выигрышей. Средисмешанных стратегий игрока Iсодержатся все его чистые стратегии. Если все числаp_iравны 0, кроме значенияp_k= 1, то эта стратегия означает выбор игроком строки с номеромk. Аналогично определяются смешанные стратегии игрокаII.

Смешанной стратегией игрока IIназывается любой упорядоченный набор из m чиселq = (q₁,q₂,…,q_m), удовлетворяющий условиям

q₁+q₂,+…+q_m=1,q_j≥ 0.

Число q_jопределяет вероятность, с которой игрокIIвыбирает столбецjматрицы выигрышей. Среди смешанных стратегий игрокаIIсодержатся все его чистые стратегии. Если все числаq_jравны 0, кроме значенияq_s=1, то эта стратегия означает выбор игрокомIIстолбца с номеромs.

Так как игроки выбирают свои чистые стратегии случайным образом, то выигрыш игрока Iбудет случайной величиной. В этом случае игрокIдолжен выбирать свои смешанные стратегии так, чтобы получить максимальныйсредний выигрыш, т.е. максимизировать математическое ожидание своего выигрыша. Аналогично, игрокIIдолжен выбирать свои смешанные стратегии так, чтобы минимизировать математическое ожидание выигрыша игрокаI. Найдем математическое ожидание выигрыша игрокаI, если он выбирает смешанную стратегиюp= (p₁,p₂,…,p_n), а игрок II – смешанную стратегиюq= (q₁,q₂,…,q_m), по формуле:

.

Стратегии

,,

называются оптимальными смешанными стратегиями игроков, если выполняются неравенства

(3.3.1)

при любых смешанных стратегиях игроков p, q. В этом случае пару стратегий (p*, q*) называют ситуацией равновесия матричной игры в смешанных стратегиях, а число v* = V(p*, q*) – значением матричной игры.

Основная теорема. Матричная игра двух лиц с нулевой суммой имеет по крайней мере одну ситуацию равновесия в смешанных стратегиях.

Теорема утверждает, что в матричной игре всегда существуют оптимальные стратегии обоих игроков.