Решение

1. Установить надстройку Поиск решения, выполнив команды: Сервис Надстройки, установить флажок Поиск решения.

2. В электронную таблицу внести исходные данные:

в ячейки C9:G14 – коэффициенты ограничений,

в ячейки J9:J14 – правые части ограничений.

3. В ячейку H5 (целевая ячейка) внести целевую функцию =G5.

4. В ячейку H9 ввести формулу =СУММПРОИЗ($C$5:$G$5;C9:G9) и копировать ее доH14.Заполнить диалоговое окно

Оптимальное распределение капитала в ячейках C5:F5:

p₁ = 0 т.е. в ГКО инвестор средства не вкладывает,

p₂ = 0,82 т.е в ГФ инвестор вкладывает 82 % капитала,

p₃ = 0 т.е. инвестор в проект 1 средства не вкладывает,

p₄ = 0,18 т.е. в проект 2 инвестор вкладывает 18 % капитала.

Оптимальное распределение капитала гарантирует инвестору ожидаемую доходность 9,53 % годовых.

3.5. Индивидуальные задания для выполнения лабораторной работы Лабораторная работа 1

Решить задачу распределения ресурсов из Вашего контрольного задания 1.

Лабораторная работа 2

Числовые данные для транспортной задачи и матричной игры определяются следующим образом. Сначала определяется номер варианта по таблице 1.1.

Первая буква фамилии	А И Т Б О Ц В	М Г Ф Д В Л Х	Е М Н Ж С Р К	Э П Щ У Ш Ю Я
№ варианта	1	2	3	4

Числовые данные внутри варианта определяется по двум последним цифрам шифра студента, N₁ –предпоследняя,N₂– последняя.

Транспортная задача.

Рассмотрим транспортную задачу, в которой в трех пунктах производства:

A₁, A₂, A₃ изготавливается однородная продукция в количествах: a₁, a₂, a₃ соответственно.

Эту продукцию требуется доставить в четыре пункта потребления: B₁, B₂, B₃, В₄ в количествах b₁ , b₂ , b₃ , b₄ соответственно.

Матрица стоимостей перевозок единицы продукции c_ij из пункта производства A_i в пункт потребления B_j:

.

Требуется определить план перевозок, который минимизирует транспортные расходы.

Вариант 1

a₁ =300+10N₁, a₂=410+ 10N₂ , a₃ =200

b₁ =200+10N₁, b₂ =300+ 10N₂ , b₃ =310, b₄=100

Вариант 2

a₁ =300+10N₁, a₂ = 410 , a₃ =200+10N₂

b₁ =200, b₂ =300+10N₁, b₃ =310, b₄ =100+10N₂ ,

Вариант 3

a₁ =300, a₂ = 410+10N₂ , a₃ =200+10N₁

b₁ =200+10N₁, b₂ = 300+ 10N₂ ,, b₃ =310, b₄=100

Вариант 4

a₁ =300 - 10N₁, a₂ = 410+10N₂ , a₃ =200

b₁ =200+ 10N₂ ,, b₂ =300, b₃ =310, b₄=100-10N₁

Матричная игра

Предположим, что инвестор составляет портфель сроком на 1 год один из 4 видов ценных бумаг:

ГО – государственные облигации,

ГФ – корпоративные ценные бумаги (голубые фишки) ,

инвестиционные проекты 1 и 2, все доходы которых поступят в конце года. Доходность инвестора зависят от состояния экономики в конце года определяется таблицей.

Вариант 1

	Спад глубокий	Спад незнач.	Стагнация	Подъем незнач.	Подъем сильный
ГО	8	8	8	8	8
ГФ	13+N1	10	9	8,5	8
Проект 1	-3	6	11+ N1	14	19
Проект 2	-2	9+ N2	12	15	26

Вариант 2

	Спад глубокий	Спад незнач.	Стагнация	Подъем незнач.	Подъем сильный
ГО	8	8	8	8	8
ГФ	13+N2	10	9	8,5	8
Проект 1	-3	6	11+ N1	14	19
Проект 2	-2	9+ N1	12	15	26

Вариант 3

	Спад глубокий	Спад незнач.	Стагнация	Подъем незнач.	Подъем сильный
ГО	8	8	8	8	8
ГФ	13	10+ N1	9	8,5	8
Проект 1	-3	6	11+ N2	14	19
Проект 2	-2+ N1	9	12	15	26

Вариант 4

	Спад глубокий	Спад незнач.	Стагнация	Подъем незнач.	Подъем сильный
ГО	8	8	8	8	8
ГФ	13	10	9	8,5+ N1	8
Проект 1	-3	6 +N1	11	14	19
Проект 2	-2	9	12+ N2	15	26

3.6. Глоссарий

Анализ чувствительности: состоит в оценке влияния параметров на оптимальные решения прямой и двойственной задач.

Базисные решения: из множества допустимых решений ЗЛП в канонической форме базисные решения получаются следующим образом:

(n-m) переменных приравниваются 0. Эти переменные назовем свободными. Значения остальных переменных получаются решением системы относительно m остальных переменных. Эти переменные назовем базисными.

Бюджетная линия – совокупность наборов товаров X=(x₁, x₂), для которых выполняется равенство называетсябюджетной линией.

Бюджетное множество – совокупность наборов товаров X=(x₁, x₂), стоимость которых не превосходит дохода M т.е. .

Взаимодополняемые товары, если выполняется условие 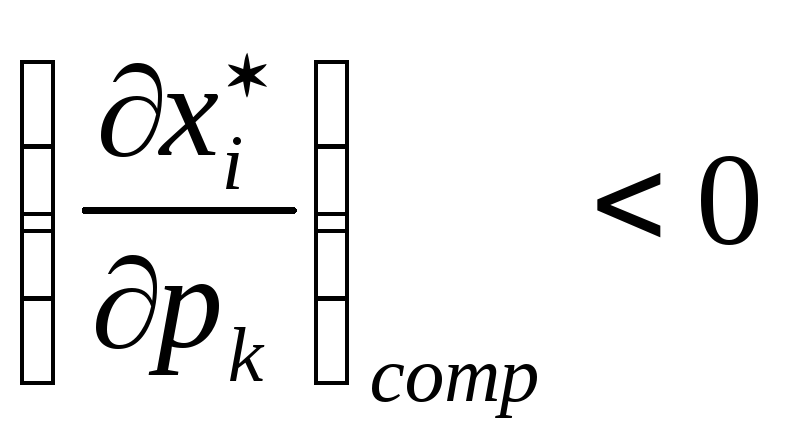, т.е. компенсированное возрастание цены одного товара приводитк одновременному уменьшению спроса на оба товара.

Взаимозаменяемые товары, если выполняется условие , т.е. компенсированное возрастание цены одного товара приводит к уменьшению спроса на этот товар и увеличению спроса на другой товар.

Выигрыш игрока I в смешанных стратегиях:

находится по формуле

.

Два ресурса взаимнодополняемые, если выполняются условия

т.е. увеличение цены одного ресурса приводит к одновременному падению спроса на оба ресурса.

Два ресурса взаимнозаменяемые, если выполняются условия

т.е. увеличение цены одного ресурса приводит к возрастанию спроса другого ресурса.

Двойственная ЗЛП для прямой задачи в канонической форме записывается в виде: найти переменные y₁, y₂,…, _,y_m, которые минимизируют функцию W

при ограничениях

переменные не имеют ограничения знака.

Допустимый план переменные x₁, x₂,…, x_m удовлетворяют всем ограничениям

,

.

Допустимое базисное решениеесли оно неотрицательно.

Двойственная транспортная задача: требуется найти переменныеu_i, v_j, которые максимизируют

при ограничениях

Задача квадратичного программирования: найти вектора X, который доставляет максимум (минимум) целевой функции

Z=CX+X^TDX

при ограничениях

AX≤B,X≥ 0.

Задача линейного программирования (ЗЛП) задача нахождения экстремума линейной функции при линейных ограничениях.

Задача нелинейного программирования состоит в определении точек максимума или минимума нелинейной функции при нелинейных ограничениях.

Задача о назначениях: найти оптимальное распределение работников по работам.

Задача потребительского выбора: найти такой потребительский набор на котором достигается максимум функции полезности

u(x₁, x₂)

при ограничениях

,

_.

Задача распределения ресурсов

требуется определить такой план выпуска продукции x₁, x₂,…, x_n, который максимизирует выручку, математически является ЗЛП в стандартной форме

Изокванта производственной функции – совокупность всех затрат ресурсов ,использование которых в производстве приводит к одинаковому объему выпуска в Y₀ единиц т.е.

Изокоста –совокупность всех векторов затрат ресурсов, использование которых в производстве приводит к одинаковым издержкам.

Интервал оптимальности: интервал изменения рыночной цены, в котором состав оптимальных базисных переменных прямой и двойственной задач не изменяется.

Интервал устойчивости запаса ресурса: интервал запаса ресурса, в котором состав оптимальных базисных переменных прямой и двойственной задач не изменяется.

Каноническая форма ЗЛП

Найти переменные x₁, x₂,…, x_n, которые максимизируют функцию

при ограничениях

Предполагается, что правые части ограничений b_i неотрицательны.

Кривая безразличия для наборов из двух товаров определяется уравнением

u(x₁, x₂) = C,

где C – любое число, u(x₁, x₂) – функция полезности.

Компенсированное возрастание цены товара обозначается

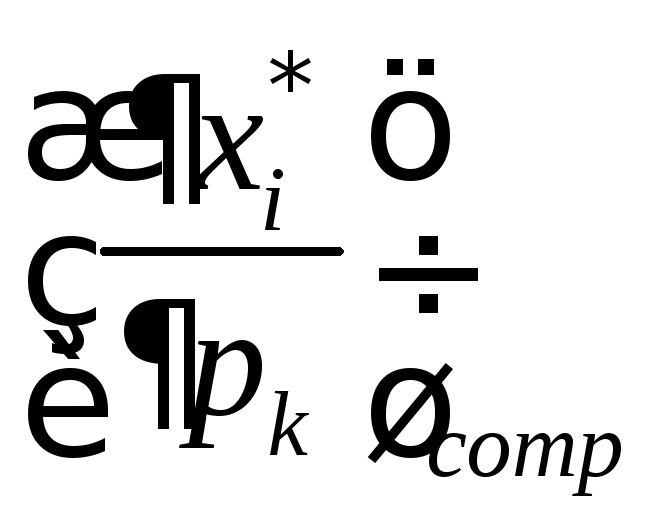
Компенсированное изменение цены товара – такое одновременное изменение цены и дохода, при котором полезность нового оптимального спроса остается прежней.

Критерий оптимальности: если для допустимых решений прямой и двойственной задач выполняется равенство целевых функций Z = W, то эти решения X и Y являются оптимальными решениями.

Коэффициенты целевой функции ЗЛП числа c₁, c₂,…, c_n целевой функции .

Коэффициент эластичности выпуска Y=f(x₁,x₂) по i-му ресурсу равен

Коэффициент эластичности E_i показывает, на сколько процентов изменяется выпуск продукции при изменении i-го ресурса на 1 %.

Линейная функция полезности для набора из двух товаров имеет вид

_.

Малоценный товар, если при возрастании дохода M спрос на этот товар не возрастает, т.е. выполняется .

Матричная антагонистическая игра двух лиц с нулевой суммой: игрок I выбирает строку номером i, а игрок II выбирает столбец с номером j, то в ситуации (i,j) выигрыш игрока I равен элементу a_ij (игрок II в этой ситуации получает выигрыш равный - a_ij).

Мультипликативная производственная функция определяется формулой

,

где число A определяет шкалу измерения выпуска продукции, параметры ₁>0, ₂ >0.

Мультипликативная функция Кобба-Дугласа определяется формулой

.

Неоклассическая мультипликативная функция

Величина a_i определяет минимальное количество приобретаемого товара. Набор (a₁,a₂) можно рассматривать как минимальную корзину потребления.

Нормальный товар, если выполняется неравенство ,т.е. с ростом его цены спрос на него падает.

Однородность степени λ производственной функции означает, что для любого λ > 0 выполняется равенство

_.

Оптимальный план x₁, x₂,…, x_m допустимый план и на нем целевая функция достигает максимального значения.

Основная теорема двойственности: решение ЗЛП следует искать среди базисных решений и на оптимальных планах всегда выполняется равенство значений целевых функций.

Отношение предпочтения означает, что «набор товаров X предпочтительнее набора товаров Y».

Предельная норма замены первого товара вторым называют величину

.

Предельная норма замены S₁₂ показывает, на сколько единиц нужно уменьшить (увеличить) количество второго товара при увеличении (уменьшении) первого товара на единицу, чтобы полезность осталась неизменной.

Предельная норма замены i –го ресурса j-м ресурсом равна

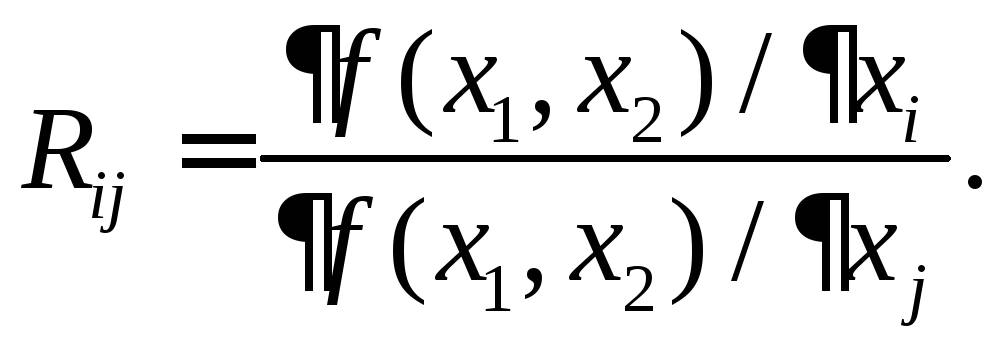
Предельная норма замены R_ij показывает, на сколько единиц нужно уменьшить (увеличить) количество j-ого ресурса при увеличении (уменьшении) i-ого ресурса на единицу, чтобы выпуск остался неизменным.

Предельная полезность товара j равна частной производной от функции полезности.

Предельная производительность i-го ресурса равна частной производной от производственной функции.

Приведенная стоимость (приведенные издержки) производства продукции j разность между удельными затратами z_j и рыночной ценой на продукцию j:

.

Производственная функция затраты-выпуск (функцию Леонтьева) задается формулой

_.

Производство продукции j убыточное, если его приведенная стоимость ,

- рентабельное, если его приведенная стоимость ;

- прибыльное, если его приведенная стоимость .

Производственной называется любая функция Y = f(x₁, x₂), которая каждому вектору затрат ресурсов X = (x₁, x₂) ставит в соответствие количество продукции Y, которое может быть получено при этих затратах.

Ресурс дефицитный, если он полностью используется в производстве.

Ресурс k ценный, если выполняется условие

Это означает, что повышение цены p на выпускаемую продукцию приводит к увеличению спроса на этот ресурс.

Ресурс k малоценный, если выполняется условие

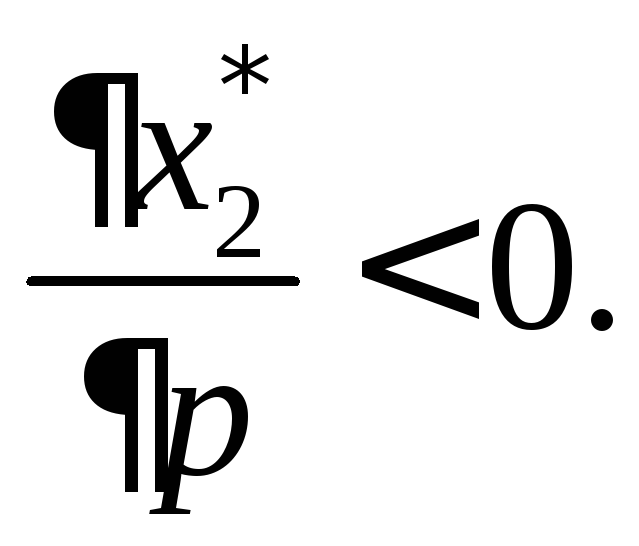
Это означает, что повышение цены p на выпускаемую продукцию к уменьшению спроса на этот ресурс.

Ресурса k нормальным, если производная т.е. при возрастании цены на ресурс спрос на него падает.

Стандартная форма ЗЛП Найти переменные x₁, x₂,…, x_n, которые максимизируют функцию

при ограничениях

Симплекс-метод: алгебраический метод состоит в построении последовательности базисных решений прямой задачи, которая приводит к оптимальному базисному решению, если оно существует.

Ситуация равновесия или седловая точка матричной игры в чистых стратегиях: найти такую ситуацию (i^*,j^*), в которой выигрыш игрокаIудовлетворяет неравенствам

a(i,j^*)≤a(i^*,j^*) ≤a(i^*,j)

для всех чистых стратегий i,j обоих игроков. Число a(i^*, j^*) является выигрышем игрока I и называется значением или ценой игры.

Смешанная стратегия игрока I: любой упорядоченный набор изnчисел p=(p₁, p₂,…, p_n),удовлетворяющий условиям

p₁+p₂,+…+p_n=1,p_i ≥ 0.

Число p_i определяет вероятность, с которой игрок I выбирает строку i матрицы выигрышей.

Смешанная стратегия игрока II: любой упорядоченный набор изmчисел q=(q₁, q₂,…, q_m), удовлетворяющий условиям

q₁+q₂,+…+q_m=1,q_j ≥ 0.

Число q_j определяет вероятность, с которой игрок II выбирает столбец j матрицы выигрышей.

Ситуация равновесия матричной игры в смешанных стратегиях:

для пары стратегий (p*,q*) выполняется неравенство для любых смешанных стратегий игроковp, q. В этом случае пару стратегий (p*, q*) называют ситуацией равновесия матричной игры, а число v*=V(p*, q*) – значением матричной игры.

Cпрос потребителя или точка локального рыночного равновесия – оптимальное решение задачи потребительского выбора.

Теневые цены соответствующие данному базисному решению:все ограничения двойственной задачи, соответствующиебазисным переменным x_j,заменяются равенствами

,

решение y₁, y₂, …,y_m полученной системы определяет теневые цены, соответст-вующие данному базисному решению.

Теорема об оценке: при изменении запаса ресурса на Δb выручка изменится на величинуZ=y Δb.

Товар – некоторая услуга, поступающая в продажу в определенное время и в определенном месте.

Товар Гиффина, если с ростом его цены спрос на него растет, т.е.

Товар Гиффина – это популярный товар, который продается по слишком низкой цене. Это вызывает сомнение в его качестве, что приводит к низкому спросу на него. Поднятие цены может повысить спрос на него.

Транспортная задача: в задаче требуется найти план перевозок {x_ij} , который минимизирует транспортные расходы

при ограничениях

, ,x _ij≥ 0

Уравнение Слуцкого

связывает изменение спроса с компенсацией и без нее.

Условия Куна-Таккера: необходимые условия существования решения задачи нелинейного программирования.

Функция полезности – любая числовая функция u, которая каждому набору товаров X сопоставляет его полезность u(X) и удовлетворяет свойству

u(X) ≥ u(Y) тогда и только тогда, когда .^.

Функция предложения–выпуск продукции в зависимости от цены выпускаемой продукцииpи цен на ресурсы w₁,w₂

.

Функции спроса на ресурсы – распределение ресурсов в зависимости от цены выпускаемой продукции p и цен на ресурсы w₁, w₂

Целевая функция ЗЛП

Целочисленное линейное программирование:

все или часть переменных должны принимать целые значения.

Ценность ресурса: теневая цена y_k показывает изменение выручки Z вызванное изменением запаса этого ресурса на 1.

Ценный товар, если при возрастании дохода M спрос на этот товар возрастает, т.е. выполняется .

Чистая стратегия игрока I в матричной игре является выбор одной из n строчек матрицы выигрышей.

Чистая стратегия игрока II в матричной игре является выбор одного из столбцов матрицы выигрышей.

Экономический смысл двойственных переменных (теневых цен) для задачи распределения ресурсов определяетстоимость единицы ресурса i.

Экономический смысл целевой функции двойственной задачи: для задачи распределения ресурсов

определяет стоимость запасов всех ресурсов в теневых ценах.

Экономический смысл левых частей ограничений двойственной задачи: для задачи распределения ресурсов

определяет стоимость ресурсов в теневых ценах, затраченных на производство единицы продукции j (удельные затраты на продукцию j).

Экономический смысл двойственных переменных транспортной задачи: переменная - u_i означает стоимость единицы продукции в пункте производства A_i, переменная v_j - стоимость единицы продукции в пункте потребления B_j, а целевая функция определяет прибыль фирмы посредника от перепродажи продукции.