Пример 4.1.1
Рассмотрим задачу о назначении четырех работниковна четыре работы. Стоимость выполнения всех работ задает матрица
Решение задачи о назначениях означает определение матрицы назначений
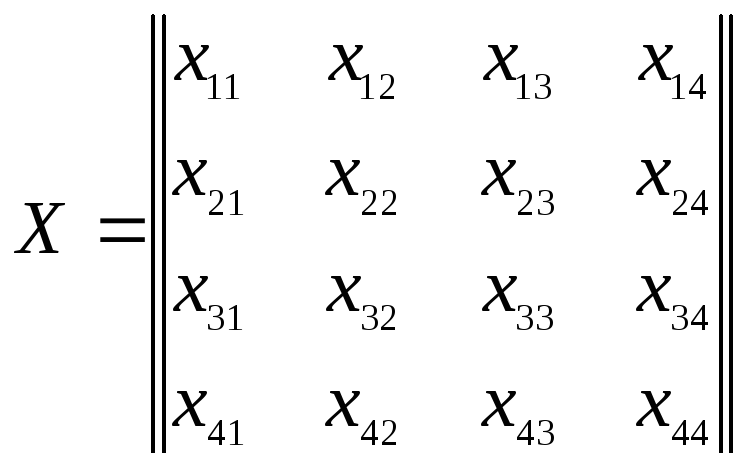
Переменная xij принимает значение 1,если работникi назначен на работуjи 0 – в противном случае.
Для решения задачи в Excelможно использовать электронные таблицы, составленные для решения транспортной задачи (табл. 4.1.1).
Таблица 4.1.1
Внесение исходных данных
В ячейках C5:F8 поместим значения матрицы стоимостейC. В ячейкиC4:F4 иB5:B8 внесем 1 (правые части ограничений). Значения в изменяемых ячейкахC12:F15 будут определять матрицу назначенийX.
формулы для матрицы назначений как показано ниже.
Внесение формул.
В ячейки B12:B15 внести формулы для суммы строк матрицыХ. В ячейкиC11:F11 внести формулы для суммы столбцов матрицыХ. В целевую ячейкуB17 внести формулу для вычисления целевой функцииZ.
Заполнить окна Поиска решения (рис. 4.1.1) и (рис. 4.1.2)
В результате получим оптимальное решение (табл. 4.1.2).
Оптимальное решение задачио назначениях состоит:
в назначении первого работника на первую работу,
в назначении второго работника на вторую работу,
в назначении третьего работника на четвертую работу,
в назначении четвертого работника на третью работу.
Стоимость работ составит 13.
Рис. 4.1.1
Рис. 4.1.2
Вопросы для самопроверки
Может ли быть переменная равна 2 в задаче о назначениях?
В чем смысл ограничений задачи о назначениях?
Объяснить смысл ограничений
Объяснить смысл ограничений
Таблица 4.1.2
4.2. Нелинейное программирование
Изучаемые вопросы:
Формулировка общей задачи нелинейного программирования;
Реализация задачи квадратичного программирования в Excel.
В дифференциальном исчислении рассматриваются необходимые и достаточные условия экстремума функций нескольких переменных. Для решения задач при наличии ограничений в виде равенств используется метод Лагранжа.
В нелинейном программировании рассматриваются задачи на экстремум с ограничениями в виде неравенств. В общей постановке задача нелинейного программирования состоит в определении точек максимума или минимума функции нескольких переменных
max (min) f(x1, x2,…, xn) (4.2.1)
при ограничениях
gi(x1,x2,…,xn) ≤ 0,i= 1, 2,…,m1,
gi (x1, x2,…, xn) ≥ 0, i = m1+ 1, m1 + 2,…, m2, (4.2.2)
gi (x1, x2,…, xn) = 0, i = m2+ 1, m2+2,…, m.
Множество (x1,x2,…,xn), для которых выполнены все ограничения (4.2.2) называется областью допустимых решений. Функцияf(x1,x2,…,xn) называется целевой функцией.
Для определения необходимых условий существования решения этой задачи используются условия Куна-Таккера. Эти условия являются достаточными, если область допустимых решений выпуклое множество, целевая функция вогнутая (выпуклая).
Рассмотрим задачу квадратичного программирования.
Введем матричные обозначения
X = (x1, x2,…, xn)T,
C = (c1, c2,…, cn),
B = (b1, b2,…, bn)T,
Задача квадратичного программирования состоит в определении вектора X, который доставляет максимум (минимум ) целевой функцииZ =C X +XT D X
при ограничениях AX ≤ B, X ≥ 0.
Если матрица D– симметрическая и положительно определенная, то целевая функция будет строго выпуклой поXв задаче минимизации. Если матрицаD– симметрическая и отрицательно определенная, то целевая функция будет строго вогнутой поXв задаче максимизации. Из линейности ограничений следует, что область допустимых решений – выпуклая. Условия Куна-Таккера для задачи квадратичного программирования являются необходимыми и достаточными. Реализация этих условий сводится к решению некоторой системы линейных уравнений. Для решения этой системы можно использовать режим Поиск решения в программе Excel.