Т а б л и ц а 3.1

Тело	Положение оси вращения	J
Полый цилиндр (обруч) Сплошной однородный цилиндр (диск) Сплошной однородный шар Сферическая оболочка Однородный тонкий стержень Однородный тонкий стержень	Ось симметрии Ось симметрии Ось проходит через центр Ось проходит через центр Ось проходит через центр тяжести Ось проходит через конец	J = mR2 J = J = J = J = J =

Момент инерции J тела относительно любой оси вращения и момент инерции J₀ тела относительно оси, параллельной данной, и проходящей через центр инерции тела, связаны соотношением (теорема Штейнера)

J = J₀ + m d ²,

где m – масса тела; d – расстояние между осями.

Поскольку угловое ускорение то

Произведение называется моментом импульса тела.

Тогда

Отсюда следует вторая формулировка основного закона динамики вращательного движения: скорость изменения момента импульса со временем равна суммарному моменту сил, действующих на тело.

Примеры решения задач

Задача 1. На барабан радиусом R = 0,5 м намотан шнур, к концу которого привязан груз m = 10 кг. Определить момент инерции барабана, если груз опускается с ускорением а = 2,04 .

Дано:

R = 0,5 м

m = 10 кг

а = 2,04

J – ?

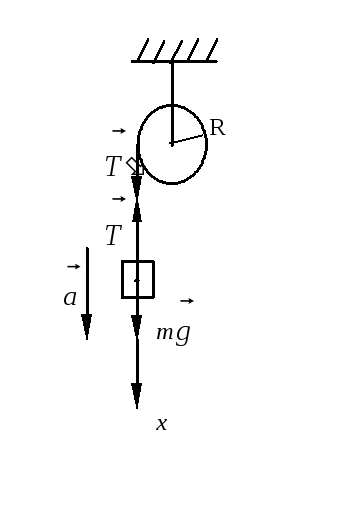
Рис. 3.5

Решение

1) Определим все силы, действующие в системе. Изобразим их на рисунке (рис. 3.5). На груз действуют силы: тяжести - вниз; натяжения нити- вверх.

На барабан действует сила натяжение нити , приложенная к ободу барабана. Эта сила создаёт вращающий момент, т.к. она приложена в точке касания нити и барабана. Плечо этой силы равноR – радиусу барабана.

На барабан, кроме того, действует сила давления на ось барабана, уравновешенная силой реакции барабана.

2) Составим уравнение движения тел системы в векторном виде:

груз:

барабан:

3) Выберем систему координат. Ось X направим по направлению ускорения груза.

Определим направление углового ускорения и момента силы. Вращение барабана происходит против часовой стрелки, значит вектор момента силы направлен перпендикулярно плоскости чертежа вверх (т.е. к нам). Пусть ось Y для барабана совпадает с направлением вектора момента силы и .

4) Запишем проекции сил на оси координат, чтобы решить векторное уравнение:

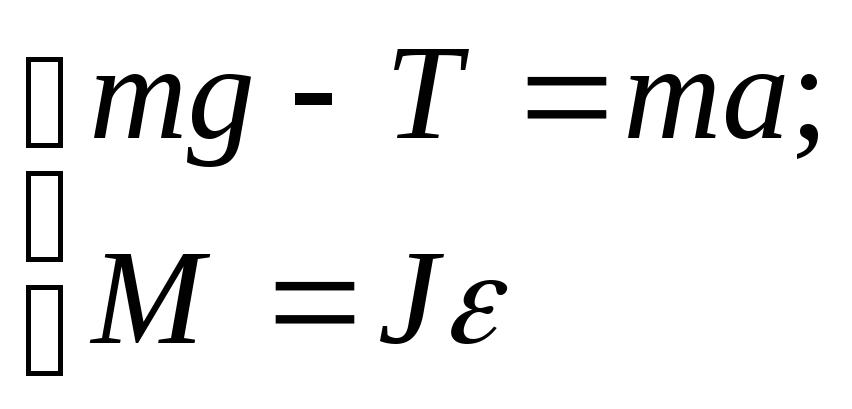(1)

Решим полученную систему:

М = Т R – численное значение момента силы, где R – плечо силы Т;

 = - связь углового и линейного ускорений барабана.

Тогда Т = m (g – a) из уравнения (1); М = m(g – a)R.

Подставив это выражение в уравнение (2), найдём

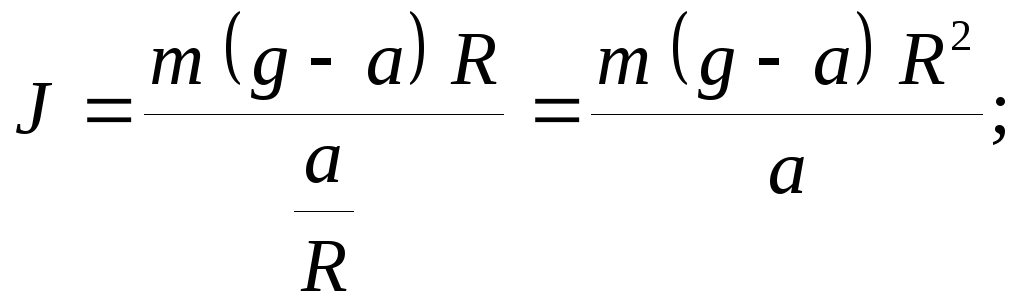
кг^.м² =9,75 кг^.м².

Ответ: момент инерции барабана J = 9,75 кг^.м2.

Задача 2. К ободу однородного диска радиусом R = 0,2 м приложена постоянная касательная сила F = 100 Н. При вращении на диск действует момент сил трения М_тр = 5 Н^.м. Найти массу диска, если известно, что диск вращается с постоянным угловым ускорением  = 100 (рис.3.6).

Д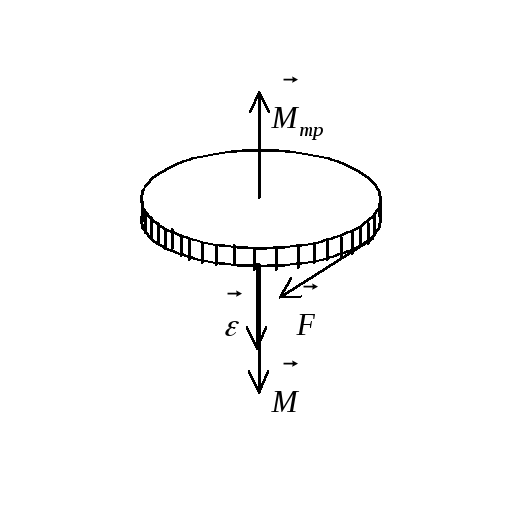ано:

R = 0,2 м

F = 100 H

M_тр = 5 Н^.м

 = 100

m -?

Рис.3.6