Примеры решения задач

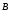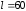Задача 1. Определить индукцию магнитного поля , созданную отрезком бесконечно длинного прямого провода в точке, равноудаленной от концов отрезка и находящейся на расстоянии см от его середины. Сила тока, текущего по проводу, А, длина отрезкасм (рис. 13.5).

Дано:

А

см = 0,6 м

см = 0,2 м

- ?

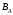Рис. 13.5

Решение

1. Каждый элемент тока в данной задаче создает индукцию , направленную в точке А перпендикулярно плоскости чертежа «к нам» (рис. 13.5).

2. Все элементарные индукции направлены одинаково в точке А, поэтому геометрическую сумму всех векторов в точке А можно заменить арифметической, т.е.

.

3. Запишем величину 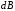(закон Био – Савара - Лапласа) в скалярной форме:

. (1)

Преобразуем так, чтобы можно было взять интеграл по. Из чертежа

.

Подставим в формулу (1):

, (2)

где r – величина переменная, зависящая от угла :

(см. рис. 13.5).

Подставив r в формулу (2), получим

. (3)

Интегрируя выражение (3) в пределах от ₁ до ₂:

;

,

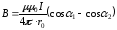где ₁ – угол между направлением начального элемента тока и направлением радиус-вектора , проведенного от элемента к данной точке (угол острый);₂ – угол между направлением конечного элемента тока и направлением радиус-вектора от элемента до данной точки (угол тупой) (см. рис. 13.5).

Из рисунка следует, что

;

.

Тогда

.

Подставим числовые значения величин:

Тл.

Ответ: Тл.

Задача 2. Два параллельных бесконечно длинных провода, по которым текут в одном направлении токи I = 60 А, расположены на расстоянии d = 10 см друг от друга. Определить индукцию магнитного поля: а) в точке, отстоящей от одного проводника на расстоянии r₁ = 5 см и от другого – на расстоянии r₂ = 12 см; б) в точке, отстоящей от I₁ и I₂ на расстояниях r₁ = r₂ = d; в) посередине между проводниками, r₁ = r₂ = .

Рис. 13.6

Решение

1. Определим направление векторов и, созданных токамиI₁ и I₂ в данной точке (рис. 13.6). перпендикуляренr₁, перпендикуляренr₂, так как r₁ и r₂ – радиусы силовых линий (от токов I₁ и I₂), а иявляются касательными к силовой линии. На рисунке токиI₁ и I₂ перпендикулярны плоскости чертежа и идут “от нас”.

2. Из рисунка видно, что . Их можно сложить геометрически, то есть по правилу параллелограмма. Величина индукции может быть найдена по теореме косинусов:

,

где  - угол между векторами 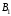и.

3. - индукция, созданная отрезком прямого бесконечного тока. Но если ток бесконечный, то (рис. 13.5):

; .

где В₁ и В₂ – индукции, созданные бесконечно прямыми токами; r₀₁ = r₁, r₀₂ = r₂ – кратчайшее расстояние от тока до точки.

.

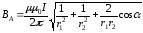Вычислим cos  : (из треугольника АВС по теореме косинусов):

.

а) Определим В_А:

Тл.

б) Если r₁ = r₂ = d, то задача упрощается (см. рис. 13.6, б):

; ;

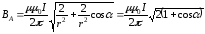(т.к.  = 60, cos  = 0,5);

Тл.

в) r₁ = r₂ = (токи параллельны) (рис. 13.7):

; ;.

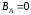r₁ = r₂ = (токи антипараллельны) (рис. 13.8):

; Тл.

Ответ: а)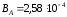Тл; б)Тл;

в) ;Тл.

Задача 3. По тонкому проводящему кольцу радиусом R = 10 см течет ток I = 80 А. Найти магнитную индукцию В в точке, лежащей: а) на оси кольца на расстоянии 17,3 см от центра кольца; б) в центре кольца.

Рис. 13.9