Магнитные индукции и напряженности простейших магнитных полей

1. Магнитная индукция и напряженность магнитного поля прямого проводника с током I на расстоянии r₀ от него (рис. 13.2):

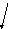
Рис. 13.2

; (13.7)

. (13.8)

где - кратчайшее расстояние от точкиС до проводника; ₁ и ₂ – углы, которые образуют радиус-векторы, проведенные в точку С из начала и конца проводника.

Для бесконечно длинного (<<l) прямого проводника ₁0, ₂, поэтому

; (13.9)

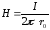. (13.10)

2. Магнитная индукция и напряженность в центре прямоугольного проводника с током:

; (13.11)

, (13.12)

где a и b – стороны прямоугольника.

3. Магнитная индукция и напряженность магнитного поля на оси кругового витка радиуса R с током I (рис. 13.3):

Рис. 13.3

; (13.13)

, (13.14)

где h – расстояние до центра витка; R – радиус витка.

Магнитная индукция и напряженность магнитного поля в центре витка (h = 0):

; (13.15)

. (13.16)

Закон Био – Савара – Лапласа и принцип суперпозиции лежат в основе первого метода расчета магнитных полей. В основе второго метода лежит теорема о циркуляции напряженности магнитного поля (закон полного тока): циркуляция вектора напряженности магнитного поля по произвольному замкнутому контуру равна алгебраической сумме токов, охватываемых этим контуром:

. (13.17)

Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого связано с направлением обхода контура правилом правого винта, ток противоположного направления считается отрицательным.

Магнитная индукция и напряженность поля короткого соленоида в произвольной точке С, лежащей на оси (рис. 13.4):

. . . . . . . . . . . . . .

++++++++++++++

₁

R

L

₂

C

I

Рис. 13.4

; (13.18)

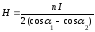, (13.19)

где 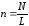- плотность витков, т.е. число витков, приходящихся на единицу длины соленоида;и- углы, под которыми из точкиС видны концы соленоида ( ):

; (13.20)

, (13.21)

где L – длина соленоида; R – радиус катушки (рис. 13.4).

Если L  R, то магнитное поле внутри соленоида однородно и линии индукции () перпендикулярны (нормальны) плоскости витков.

Такой соленоид называется бесконечно длинным или нормальной катушкой. Индукция и напряженность магнитного поля длинного соленоида рассчитывается по формулам

; (13.22)

. (13.23)

Методика расчета магнитных полей проводников с током заключается в следующем:

1. Определить направление магнитных индукций, созданных элементами тока в данной точке, пользуясь правилом векторного произведения, или правилом обхвата правой руки.

2. Записать выражение закона Био – Савара – Лапласа для каждой из составляющих индукции (напряженности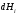), созданных элементами тока в данной точке.

3. Геометрически сложив элементарные индукции (напряженности), создаваемые всеми элементами тока, определить величину индукциирезультирующего поля, созданного в данной точке:

. (13.24)

Этот метод справедлив и для определения индукции (напряженности) магнитного поля, созданного несколькими проводниками с током конечной длины и разной геометрии.