Решение (рис.8.4, 8.5).

Рис.8.4 Рис.8.5

Линии индукции начинаются на заряде q, и плотность линий не изменяется при переходе из парафина в воздух.

Линии напряжённости тоже начинаются на зарядеq, но плотность линий изменяется при переходе из парафина в воздух в 2 раза (= 1; = 2).

2. Бесконечно длинная тонкостенная металлическая трубка радиусом R = 2 см равномерно заряжена с поверхностной плотностью заряда  = 10^-3 . Определить напряжённость электрического поля в точках, отстоящих от оси на расстояниях: а)= 1 см; б)=R = 2 см; в) = 3 см. Построить графики зависимостейD и E от r.

Дано:

R = 2 см = 2 ^.10^-2 м

 = 10^-9 Кл/м²

= 10^-2 м

2 ^.10^-2 м

= 3 ^.10^-2 м

 = 1

Е₁ - ? Е₂ - ? Е₃ - ?

D₁ - ? D₂ - ? D₃ - ?

Решение

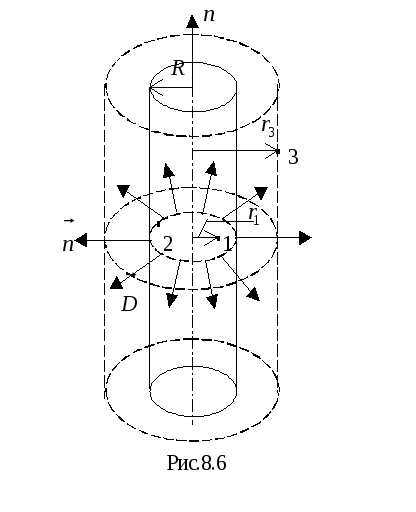
1. Изобразим на рисунке силовые линии поля цилиндра. Линии начинаются на поверхности трубки и идут по радиусам перпендикулярно поверхности (боковой) цилиндра (рис.8.6).

2. Исходя из этих соображений, охватывающая заряд поверхность должна быть цилиндрической, тогда перпендикулярен боковой поверхности,cos = 1, т.к.  = () = 0.

Поток через основания трубки равен нулю, т.к.  = () = 90⁰, cos = 0.

Для точки 1 поверхность, проходящая через точку, тоже цилиндрическая, радиус основания цилиндра равен . Заряда же внутри металлической трубки быть не может. Поэтому

Следовательно,

D S₁ = 0; D = 0 и E = 0.

Точка 2. Охватывающая поверхность – цилиндра радиусом R; охваченный поверхностью заряд q =  S₂, где  - поверхностная плотность заряда.

где h – высота цилиндра.

D S₂ = q; D S₂ =  S₂; D =  ;

Точка 3. Поток через поверхность, проходящую через точку 3,

Заряд, охваченный поверхностью,

Приравниваем по теореме Остроградского – Гаусса:

Построим графики зависимостей D и E от r (рис. 8.7, 8.8).

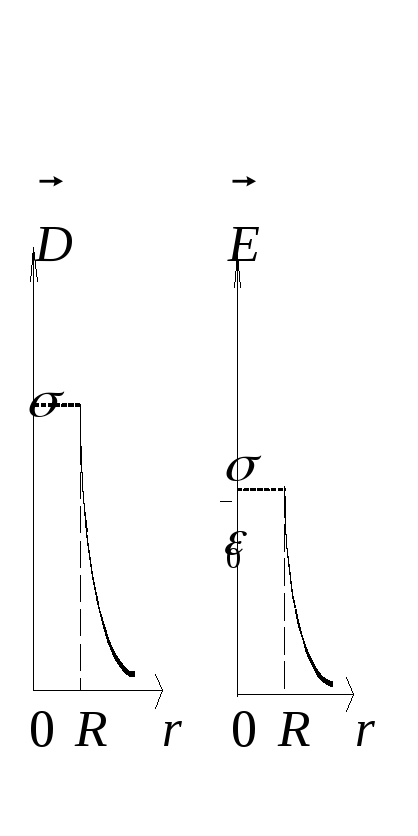
Рис.8.7 Рис.8.8

Напряжённость и индукция электрического поля внутри цилиндра равна нулю, а снаружи, начиная с поверхности, убывает обратно пропорционально расстоянию.

Ответ: а) D₁ = 0; E₁ = 0; б) D₂ =10^-9 ; E₂ = 1,12 ^.10² ;

в) D₃ = 6,7 ^.10^-10 E₃ = 75,5 .

3. На металлической сфере радиусом R = 10 см находится заряд q = 10^-9 Кл. Определить напряжённость электрического поля в точках: а) на расстоянии = 8 см от центра сферы; б) на поверхности её; в) на расстоянии= 15 см от центра сферы (рис.8.9). Построить графики зависимостейE и D от r.

Дано:

q = 10^-8 Кл

R = 10 см =10^-1 м

= 8 см = 8 ^.10^-2 м

= R =10 см = 0,1 м

= 15 см = 0,15 м

Е₁ - ? Е₂ - ? Е₃ - ?

Рис.8.9

Решение

Зарядов внутри сферы нет, линии индукции начинаются на её поверхности. Поле сферически симметричное, как у заряженного шара.

Охватывающей поверхностью будет сфера, проходящая через заданную точку, т.к. перпендикулярен к сферической поверхности.

а) Сфера, проведённая через точку 1 (r < R) не охватывает никаких зарядов, следовательно, q = 0, = 0,D₁ = 0 , Е₁ = 0.

б) Сфера, проведённая через точку 2 (r = R), охватывает весь заряд, находящийся не её поверхности:

Поток линий индукции через эту поверхность

Ф_e2 = D₂ S₂ = D₂ 4R².

Тогда по теореме Остроградского – Гаусса

в) Сфера, проведённая через точку 3, охватывает тоже весь заряд, находящийся на поверхности металлической сферы:

Поток

Тогда

Отсюда следует, что напряжённость, созданная заряженной сферой на её поверхности и вне сферы, такая, которую создал бы точечный заряд, если бы он был расположен в центре сферы. Графики зависимости D и E от r приведены на рис.8.10 и 8.11.

Рис.8.10 Рис.8.11

Ответ: а) D₁ = 0; E₁ = 0; б) D₂ = 8 ^.10^-8 ;E₂ = 900 ;

в) E₃ = 400 .

4. К бесконечной плоскости, вдали от её краёв, подвешен на шёлковой нити шарик массой m = 2 г. Шарик заряжен электрическим зарядом того же знака, что и плоскость. Определить заряд шарика, если нить образует с плоскостью угол 30⁰. Поверхностная плотность заряда плоскости  = 6,7 ^.10^-5 (рис.8.12).

Дано:

 = 6,7

m = 2 г = 2 ^.10^-3 кг

= 30⁰

q - ?