Занятие 7.

ЗАКОН КУЛОНА. ПРИНЦИП СУПЕРПОЗИЦИИ ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ

Учебная цель: добиться понимания физической сущности закона Кулона и принципа суперпозиции электростатических полей. Привить навыки самостоятельного решения задач по данной теме.

Литература

Основная: Детлаф А.А., Яворский Б.М. Курс физики.  М.: Высшая школа, 1989. -

Гл.13, § 13.1 – 13.3, § 13.5.

Дополнительная: Савельев И.В. Курс общей физики. – М.: Наука, 1989. – Т.2, гл.1, § 1, 2, 5.

Контрольные вопросы для подготовки к занятию

1. Дайте определение, назовите основные свойства и единицу измерения электростатического заряда.

2. Сформулируйте и запишите закон сохранения заряда.

3. Какой заряд называется точечным?

4. Сформулируйте и запишите закон Кулона.

5. Как направлена сила взаимодействия точечных электрических зарядов?

6. Что называется электростатическим полем? Каковы его характеристики?

7. Что называется напряженностью? От чего зависит величина напряженности? Какова единица измерения напряженности в СИ?

8. По какой формуле рассчитывается напряженность точечного заряда (заряженной сферы)?

9. Сформулируйте и поясните принцип суперпозиции электростатических полей.

Краткие теоретические сведения и основные формулы

Электрический заряд – физическая величина, определяющая интенсивность электромагнитного взаимодействия заряженных частиц. Единица электрического заряда в СИ – кулон (Кл). 1 Кл – электрический заряд, проходящий через поперечное сечение проводника при токе силой 1 А за время 1 с,

q = I t. (7.1)

Опытным путём американский физик Р. Милликен установил, что электрический заряд дискретен, т.е. заряд любого тела составляет целое кратное от элементарного электрического заряда е (е = 1,6 ^.10^-19 Кл). Электрон (m_e = 9,11кг) и протон (m_p = 1,67кг) являются соответственно носителями элементарных отрицательного и положительного зарядов.

Из обобщения опытных данных был установлен фундаментальный закон природы, впервые сформулированный английским физиком М. Фарадеем, закон сохранения заряда:

алгебраическая сумма электрических зарядов любой замкнутой системы остаётся постоянной, какие бы процессы ни происходили внутри этой системы:

(7.2)

Замкнутой называется система, не обменивающаяся зарядами с внешними телами.

Точечным называется заряд, сосредоточенный на теле, размеры которого пренебрежимо малы по сравнению с расстоянием до других заряженных тел, с которыми он взаимодействует.

Взаимодействие точечных зарядов подчиняется закону Кулона.

Закон Кулона

сила взаимодействия между двумя точечными зарядами пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними:

(7.3)

где  - относительная диэлектрическая проницаемость среды – величина, показывающая во сколько раз сила взаимодействия между зарядами в данной среде меньше силы взаимодействия между ними в вакууме.

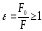(7.4)

Для вакуума = F и  = 1.  - величина безразмерная, табличная; k–коэффициент пропорциональности, зависящий от выбора системы единиц. В СИ он принимается равным где= 8,85- электрическая постоянная.

Тогда

(7.5)

Закон Кулона также справедлив для взаимодействующих заряженных тел сферической формы. В этом случае r – расстояние между их центрами.

Сила направлена по прямой, соединяющей центры взаимодействующих зарядов, то есть является центральной. Она соответствует притяжению (F 0) в случае разноимённых зарядов и отталкиванию (F  0) в случае одноимённых зарядов (рис.7.1).

Рис.7.1

Особый вид материи, являющейся носителем взаимодействия неподвижных электрически заряженных тел, называется электростатическим полем.

Электростатическое поле исследуется с помощью пробных зарядов. Пробным зарядом называется заряженное тело, настолько малое, что оно практически не вызывает (вследствие индукции) перераспределения зарядов на окружающих телах.

Электростатическое поле имеет две характеристики: силовую – напряжённость , энергетическую – потенциал.

Напряженность электростатического поля в данной точке есть физическая величина, определяемая силой, действующей на единичный положительный пробный заряд, помещенный в эту точку поля:

. (7.6)

Направление вектора совпадает с направлением силы, действующей на положительный заряд. Единица напряженности электростатического поля – Ньютон на Кулон (Н/Кл): 1 Н/Кл – напряженность электростатического поля в точке, в которой на пробный заряд 1 Кл действует сила 1 Н (1 Н/Кл = 1 В/м).

Напряженность поля точечного заряда q выражается формулой

(7.7)

Напряженность пропорциональна заряду, создающему поле, и характеризует электростатическое поле в той точке, где пробный заряд находится, но не зависит от пробного заряда.

Для наглядности электростатическое поле изображают с помощью линий напряженности (силовых линий), которые проводят так, чтобы касательные к ним в каждой точке пространства совпадали по направлению с вектором напряженности в данной точке поля (рис.7.2).

Рис.7.2

Условились считать, что силовые линии выходят из положительно заряженных тел и входят в отрицательно заряженные. Линии напряженности точечного заряда представляют собой радиальные лучи (рис.7.3).

Рис.7.3

Густота силовых линий принимается за величину напряженности.

Поле называют однородным, если во всех его точках напряженность одинакова и по величине, и по направлению (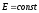). Оно изображается прямыми параллельными линиями, идущими на равных расстояниях друг от друга (например, поле плоского конденсатора).

Принцип суперпозиции электрических полей: напряженность результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке А каждым из зарядов в отдельности:

(7.8)

Принцип суперпозиции лежит в основе одного из методов расчёта электростатических полей.

Напряженность поля точечного диполя:

1. в общем случае (рис.7.4):

Рис.7.4

(7.9)

где 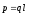- электрический момент диполя (дипольный момент);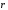- радиус-вектор, проведенный от центра диполя к точкеА, в которой рассматривается напряженность;  - угол между плечом диполя и радиусом-вектором.

2. в точке, лежащей на оси диполя ( = 0):

(7.10)

3. в точке, лежащей на перпендикуляре к плечу диполя, восстановленному из его середины :

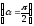(7.11)

Механический момент, действующий на диполь с электрическим моментом , помещённый в однородное электростатическое поле напряжённостью:

(7.12)

или М = рЕ sin , (7.13)

где  = [] – угол между направлением вектора электрического моментаи вектором напряженности.