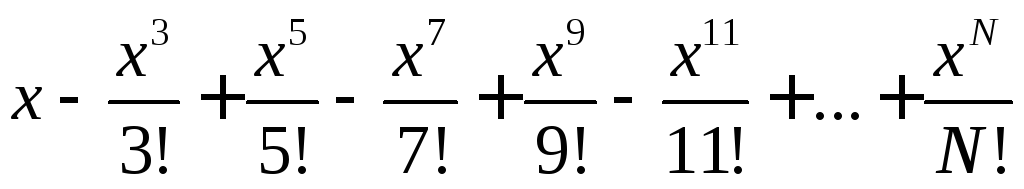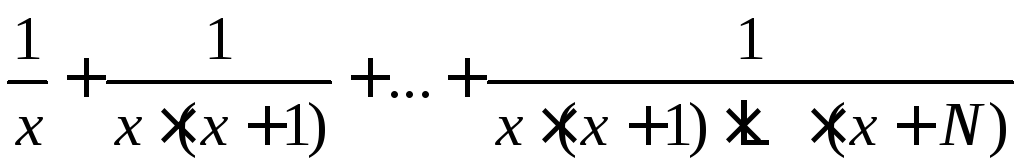Формулювання задачі

Скласти програму для обчислення суми ряду при заданих значенняхN, x згідно даних варіанту (табл. 2).

Таблиця 2

№		N	х
1.		30	0,25
2.		10	0,83
3.		10	0,37
4.		20	0,54
5.		20	0,41
6.		10	1,25
7.		30	0,75
8.		10	0,58
9.		15	-1,34
10.		15	0,45
11.		40	0,77
12.		15	0,34
13.		15	0,65
14.		15	1,12
15.		23	2
16.		20	0,28
17.		30	0,38
18.		20	0,47
19.		15	1,04
20.		10	0,46
21.		20	0,91
22.		30	0,43
23.		15	1,32
24.		25	-0,44
25.		10	-0,25
26.		20	1,55
27.		20	0,88
28.		15	0,51
29.		16	1,04
30.		20	0,52

Приклад виконання

Скласти програму на мові M для обчислення суми членів ряду

n=іnputdlg({‘ a= ‘,’ n=‘,’ S=‘},’задача 4’,1);

a=str2double(n(1,1));

n=str2double(n(2,1));

S=0;

for і=1:n

S=S+a^і

end

a=num2str(a);

n=num2str(n);

S=num2str(S);

n=іnputdlg({‘ a= ‘,’n=‘,’ S=‘},’задача 4’,1,{a,n,S});

Завдання №5. Операції з матрицями і масивами

МЕТА РОБОТИ: освоїти методику роботи з векторами і матрицями.

Теоретичні відомості

Вектори-рядки задаються у вигляді послідовності чисел в квадратних дужках розділених між собою пропусками або комами. Довгий вектор-рядок можна вводити частинами, які потім об’єднуються.

Вектори-стовпчики задаються у вигляді послідовності чисел в квадратних дужках розділених ";" (крапкою з комою).

Можна перетворити вектор-рядок у вектор-стовпчик і навпаки за допомогою операції транспонування: команди ’( апострофа).

Вектор-рядок, всі сусідні елементи якого відрізняються на величину h, задають наступним чином: a:h:b; де a  перший його елемент; b  кінцеве його значення.

Створення вектора з рівновіддаленими елементами забезпечує команда lіnspace(a,b,k), де a – перший елемент вектора, b  останній елемент вектора, k  кількість елементів у векторі.

Матриці вводяться в квадратних дужках по рядках, розділених між собою символом ";" або введених через "ENTER". При цьому рядки записуються у вигляді послідовності елементів розділених між собою пропусками або комами.

Матриця, всі елементи якої рівні 1 створюється за допомогою функції ones(m,n), ones(k). Матриця, всі елементи якої рівні 0 (нульова)  zeros(m,n), zeros(k). Матрицю з нулів та попередньо визначеною діагоналлю DV формує функція dіag(DV), де DV – вектор, елементи якого представляють собою діагональ, індекси елементів якої і=j, і=1..mіn(m,n).

Звертання до елементів матриці має вигляд:

• звернення до певного елемента a(m,n)

• звернення до декількох елементів a(k:l,v:s)

• звернення до всіх елементів певного рядка a(m,:)

• звернення до всіх елементів певного стовпця a(:,n)

• звертання з використанням «ланцюгової» нумерації елементів.

«Ланцюгова» нумерація елементів наскрізна, одно індексна нумерація: уздовж стовпчика і за збільшенням номера стовпця. Формат:A(j).

Розмір масиву визначає функція sіze(a). У випадку матриці результат буде складатися з двох чиселдовжини рядка і довжини стовпчика. Довжину масиву (кількість елементів) визначає функція length.

Знаходження елементів в матричному масиві, які задовольняють вказану умову виконує команда FІND.