2. Дифференциальное исчисление функций
ОДНОЙ ПЕРЕМЕННОЙ
2.1. Определение производной
Производной
функции
в точке
называется предел отношения приращения
функции
в этой точке к приращению аргумента
,
когда приращение аргумента стремится
к нулю.
Если этот предел
конечный, то функция называется
дифференцируемой
в точке
.
Производная функции
в точке
обозначается одним из следующих символов:
или
- Г.В.Лейбниц;
или
- Ж.Л.Лагранж.
Итак, по определению,
. (2.1)
Операция
нахождения производной от функции
называетсядифференцированием
этой функции.
2.2.Основные правила дифференцирования функций
1. Производная алгебраической суммы
.
2. Производная произведения
,
в частности
.
3. Производная отношения
,
,
в частности
.
4. Производная сложной функции
,
где
.
5. Производная показательно-степенной функции
,
,
.
2.3. Таблица производных основных функций
1. 
.
2. 
,
в частности
,
,
.
3. 
,
в частности
.
,
в частности
;
.
6.
.
.
8.
.
.
10.
.
11.
.
12.
.
2.4. Решение типовых примеров заданий 3, 4 РГР
Найти производные
пользуясь формулами и правилами
дифференцирования.
1.
.
Решение. Преобразуем данную функцию и применим правила нахождения производной алгебраической суммы функций
.
.
2.
.
Решение. Применим правила нахождения производной произведения функций
.
3.
.
Решение. Применим правила нахождения производной отношения функций
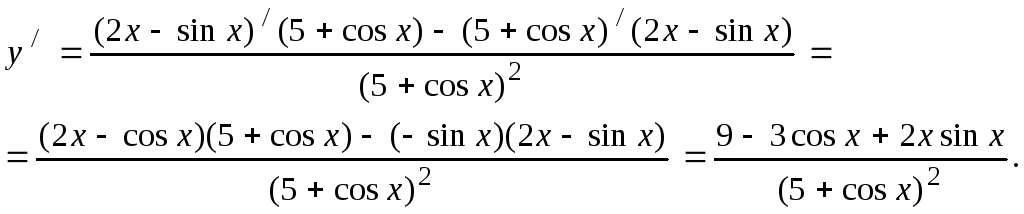
4.
.
Решение. Применим правила нахождения производной сложной функций
.
5.
.
Решение.
1-й способ. Воспользуемся правилом нахождения производной показательно-степенной функции
.
Обозначим
;
.
.
2-й способ.Показательно степенную функцию предварительно прологарифмируем, а затем вычислим производную полученного равенства.
;
;
.
6.
.
Применим логарифмичес-кое дифференцирование.
.
.
.
7.
.
Решение.
Данная функция задана неявно. Вычислим
производную равенства при условии, что
– аргумент,
,
а затем найдём
.
;
;
.
2.5. Раскрытие неопределенностей по правилу Лопиталя
Правило Лопиталя
применяется для раскрытия неопределенностей
и
.
Если при
функции
и
одновременно стремятся к
или
,
то предел отношения равен пределу
отношения их производных, т.е.
.
При этом предполагается,
что функции
и
существуют и конечны.
Если же отношение
производных также будет представлять
случай
и
,
можно снова и снова применять правило
Лопиталя.
Если имеются
неопределенности типа
или
,
то сначала приводят эти функции к виду
дроби, которая представляет неопределенность
и
,
а затем уже используется правило
Лопиталя.
Нахождение предела
функции в случае неопределенностей
вида
,
,
с помощью логарифмирования также
сводится сначала к случаям
или
,
затем уже используется правило Лопиталя.
2.6. Решение типовых примеров задания 5 ргр
Найти пределы, используя правило Лопиталя. Сравнить результаты с решениями задания 1.
1.
.
Решение.
Неопределенность вида
.
Используем правило Лопиталя.
.
2.
.
Неопределенность вида
.
Решение.
.
3.
.
Неопределенность вида
.
Решение.
=
.
4.
.
Неопределенность
вида
.
Решение.
.
5.
.
Неопределенность
вида
.
Решение.
.
6.
.
Решение.
Неопределенность
вида
.
Прологарифмируем данную функцию
сведем неопределенность к виду
и применим правило Лопиталя
;
.
Отсюда
;
.
Ответы совпадают с результатами решения примеров задания 1.