
89 2 . Клистроны
2. Клистроны
Проведенный выше анализ показывает, что для достижения наибольшей эффективности взаимодействия электронного потока с электрическим полем последнее следует концентрировать ввозможно меньшем объеме и пропускать промодулированный по плотности электронный поток вдоль направления силовых линий этого поля. Длина пространства взаимодействия должна быть при этом по возможности более короткой. Для компенсации кратковременности взаимодействия заряда с полем его напряженность надо по возможности увеличить, что достигается обычно применением высокодобротных резонаторов.
Следование этим рекомендациям привело к созданию класса приборов с сосредоточенными полями – клистронов, триодов идиодов диапазона СВЧ, которые широко используются во многих радиоэлектронных устройствах для усиления и генерирования сверхвысокочастотных сигналов.
Клистрон – первый высокочастотный прибор, в котором использовался принцип фазовой фокусировки. В клистроне все характерные для сверхвысокочастотных приборов процессы – модуляция электронного потока по скорости, группирование иотбор энергии высокочастотным полем от сгруппированного пучка – осуществляются раздельно и могут быть рассмотрены в наиболее упрощенном виде.
Подразделяются клистроны на пролетные и отражательные.
2.1. Двухрезонаторный пролетный клистрон
Схема двухрезонаторного пролетного клистрона приведена на рис. 2.1,а.
Первый резонатор клистрона служит для модуляции электронного пучка по скорости и называется группирователем.
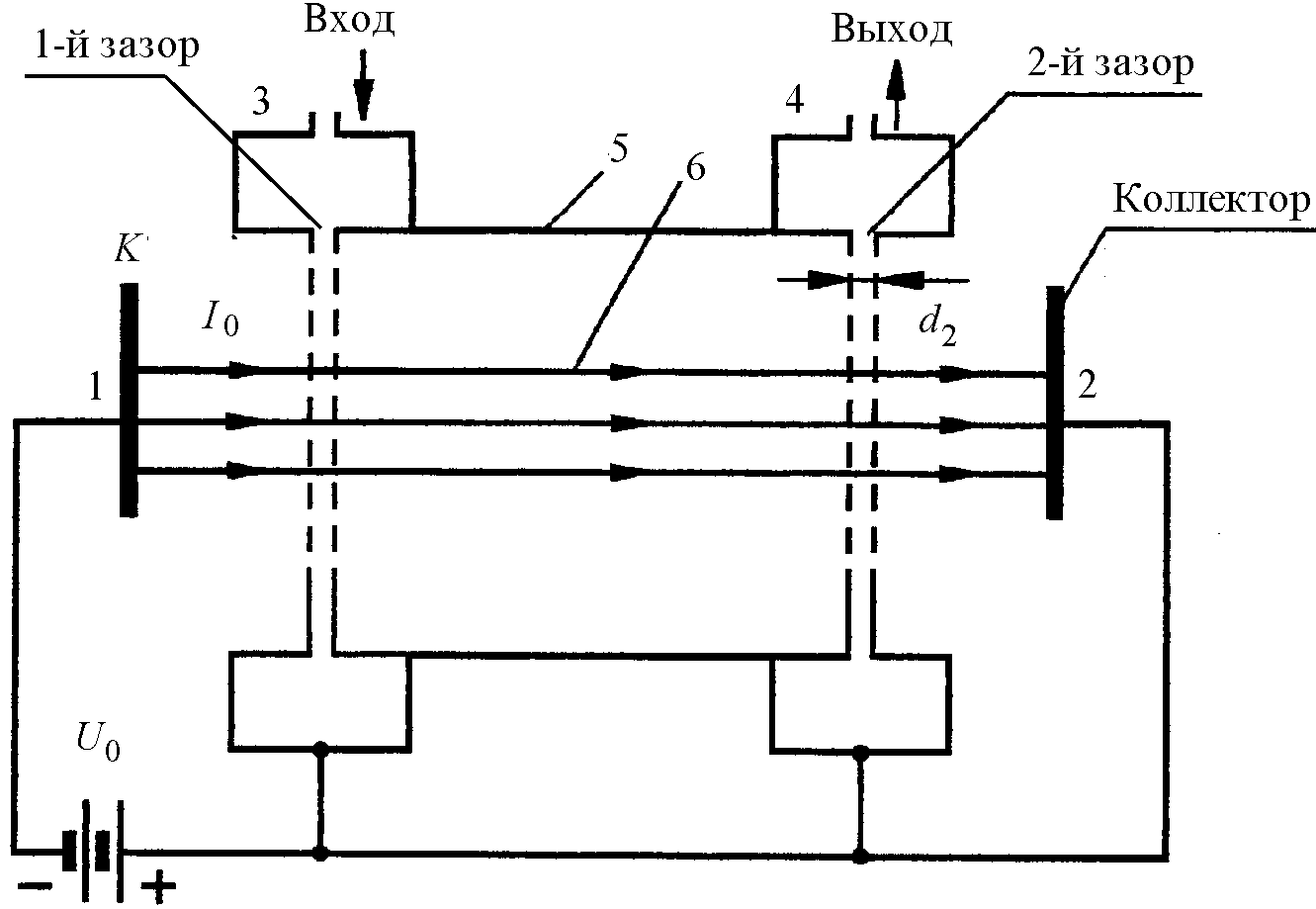
Рис. 2.1,а. Схема устройства двухрезонаторного клистрона: 1 – катод; 2 – коллектор; 3, 4 – входной и выходной резонаторы; 5 – труба дрейфа; 6 – электронный поток
Второй резонатор служит для отбора высокочастотной энергии от пучка, имеющего модуляцию по плотности. Металлическая труба, находящаяся между двумя резонаторами, экранирует пространство дрейфа от внешних постоянных и переменных полей.
2.1.1. Принцип действия двухрезонаторного пролетного клистрона
Немодулированный электронный поток, выходящий из катода, поступает в первый резонатор. Сигнал, вводимый с помощью петли связи в этот резонатор, возбуждает в нем высокочастотное напряжение, модулирующее проходящий через него электронный пучок по скорости. Двигаясь далее в пространстве дрейфа, электроны постепенно образуют сгустки. Очевидно, что частота следования сгустков равна частоте сигнала. Пролетая между сетками выходного резонатора, сгустки вызывают в нем наведенный ток той же частоты. Если собственная частота выходного резонатора равна частоте сигнала, то наведенный ток создает напряжение между сетками резонатора, в результате чего появляющееся электрическое поле тормозит электроны.Кинетическая энергия электронов, полученная ими от источника ускоряющего напряжения U0, преобразуется в энергию СВЧ колебаний и поступает через вывод энергии в выходную нагрузку. Электроны, прошедшие через второй зазор, оседают на коллекторе и рассеивают на нем в виде тепла оставшуюся кинетическую энергию.
Основные отличия клистрона от «обычных» ламп:
1) отказ от электростатического управления электронным потоком и использование динамического управления, основанного на скоростной модуляции и группировке электронов;
2) использование принципа наведения тока в выходном зазоре и разделение функций выходного зазора и коллектора;
3) применение полых резонаторов, органически связанных с входным и выходным зазорами и более всего отвечающих требованиям диапазона СВЧ;
4) выделение катода из состава высокочастотной цепи и расположение ускоряющего промежутка перед высокочастотным управляющим зазором.
2.1.2. Кинематическая теория группировки электронов при использовании преобразования методом дрейфа
Рассмотрим более детально процессы, происходящие в пространстве дрейфа двухрезонаторного клистрона [1].
Идеализированная схема двухрезонаторного клистрона представлена на рис. 2.1,б. Высокочастотный зазор резонатора может иметь разную конструкцию: сеточную и бессеточную. В данном случае входной и выходной зазоры выполнены в виде двух пар идеальных плоских сеток, прозрачных для электронов и непрозрачных для электрического поля. Расстояние между сетками равно соответственно d1иd2. Электроны ускоряются постоянным напряжениемU0и двигаются далее по инерции. Модуляция по скорости в первом зазоре производится высокочастотным напряжением, амплитуду которого будем полагать много меньшей постоянного напряженияU1 <<U0.
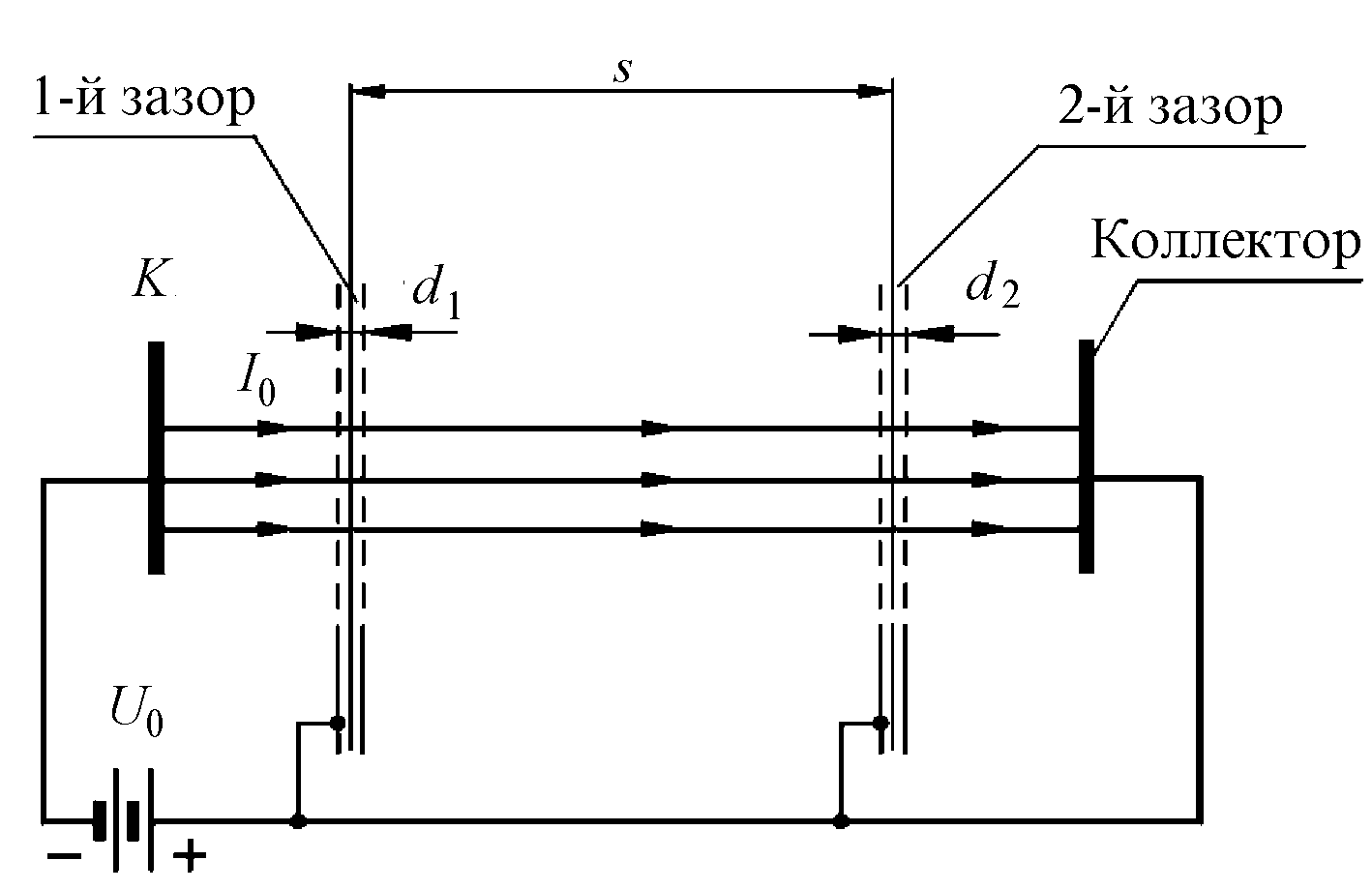
Рис. 2.1,б. Идеализированная схема двухрезонаторного клистрона
Обозначим через t1момент времени, в который рассматриваемый электрон проходит центр первого зазора. В дальнейшем индексом 1 будем обозначать все величины, относящиеся к первому зазору. Соответственно индексом 2 будем обозначать величины, характеризующие состояние пучка и поля во втором зазоре.
Таким образом, мгновенное значение модулирующего напряжения на первом зазоре может быть записано в виде
u=U1sint1;![]() . (2.1)
. (2.1)
Скорость электронов vна выходе из первого зазора определяется уравнениями скоростной модуляции. При принятых здесь обозначениях имеем
v=v0 +v1sint1; (2.2)
v1 =v0![]() ,
(2.3)
,
(2.3)
где v0
=![]() .
ЧерезМ1обозначен коэффициент
связи электронного пучка с полем первого
зазора, определяемый согласно уравнению
(1.4) через угол пролета1в первом зазоре в виде
.
ЧерезМ1обозначен коэффициент
связи электронного пучка с полем первого
зазора, определяемый согласно уравнению
(1.4) через угол пролета1в первом зазоре в виде
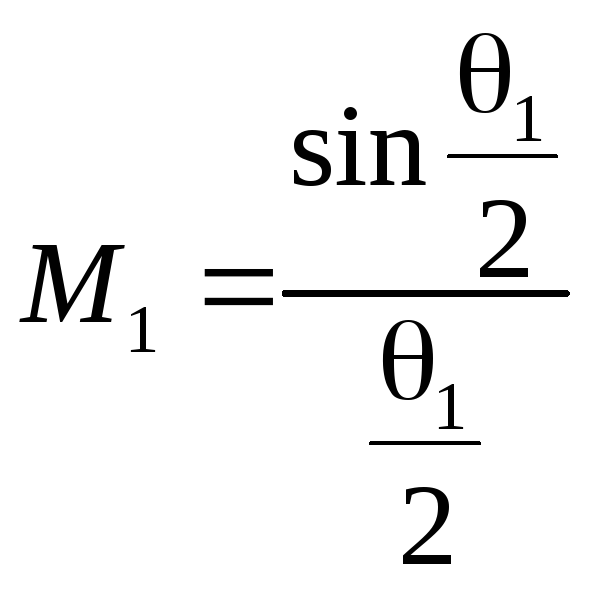 ,
где
,
где![]() .
(2.4)
.
(2.4)
Найдем момент времени t2, при котором электрон, прошедший центр первого зазора в момент времениt1, входит во второй зазор
![]() ,
(2.5)
,
(2.5)
где s– длина пространства дрейфа между центрами первого и второго резонаторов.
Имея в виду, что величина v1много меньше постоянной скоростиv0,
преобразуем уравнение (2.5), вынося во
втором члене множитель![]() и раскладывая второй множитель в ряд
по малому параметру,
и раскладывая второй множитель в ряд
по малому параметру,
![]() wt1)-1»
wt1)-1»![]() .
(2.6)
.
(2.6)
Обе части полученного уравнения умножим на угловую частоту сигнала . Таким образом, в линейном приближении фаза прибытия электрона во второй резонаторt2в зависимости от фазы прохождения тем же электроном первого резонатораt1 будет определяться выражением
![]() .
(2.7)
.
(2.7)
Введем обозначение
![]() .
(2.8)
.
(2.8)
Безразмерная величина Xназывается параметром группирования. Выражение (2.8) с учетом (2.3) можно записать в виде
X=![]() ,
(2.9)
,
(2.9)
где – угол пролета в пространстве дрейфа для электрона, не изменившего своей скорости в первом резонаторе, равный
![]() .
(2.10)
.
(2.10)
Таким образом, параметр группирования Хпропорционален углу пролета в пространстве дрейфа и отношению эффективного модулирующего напряжения на первом зазоре к ускоряющему напряжению клистрона.
Используя обозначения (2.8) и (2.10), можно переписать полученную выше зависимость в виде
![]() .
(2.11)
.
(2.11)
Остановимся подробнее на этом уравнении,
определяющем фазу прибытия электрона
во второй резонатор. В отсутствие
высокочастотного напряжения (при U1=0) параметрХ= 0, а фаза прибытия
электронов во второй зазор линейно
связана с фазой прохождения теми же
электронами через первый зазор![]() и никакой группировки электронов
не происходит. ЕслиU1 ¹0 иМ1 ¹0, то при конечной величинепараметрХотличен от нуля. Зависимость
фазы прибытия во второй зазор от фазы
прохождения через первый зазор согласно
уравнению (2.11) перестает быть линейной.
Это означает, что происходит периодическое
уплотнение или группировка электронного
потока.
и никакой группировки электронов
не происходит. ЕслиU1 ¹0 иМ1 ¹0, то при конечной величинепараметрХотличен от нуля. Зависимость
фазы прибытия во второй зазор от фазы
прохождения через первый зазор согласно
уравнению (2.11) перестает быть линейной.
Это означает, что происходит периодическое
уплотнение или группировка электронного
потока.
Явление группировки, когда «быстрые электроны догоняют медленные», было пояснено с помощью пространственно-временной диаграммы на рис. 1.11.
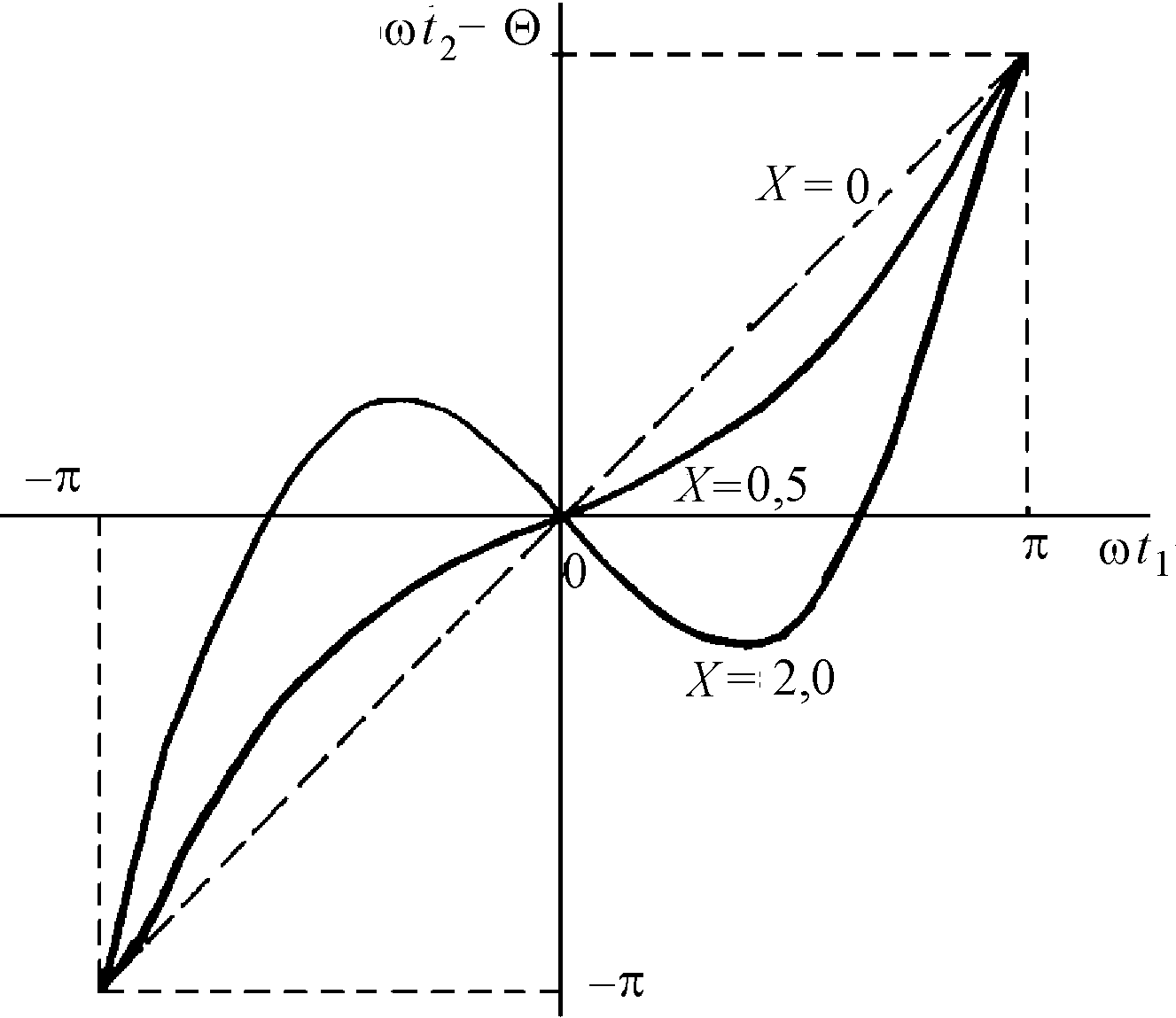
Рис. 2.2. График зависимости фазы прибытия электрона во второй резонатор от фазы прохождения того же электрона через первый резонатор пролетного клистрона
На рис. 2.2 приведен график, построенный по уравнению (2.11) для трех значений параметра группировки Х. Чем больше величинаХ, тем сильнее график фазы прибытия отклоняется от прямой линии.
В свою очередь, значения Х характеризуют различные режимы группирования электронов и определяют форму волны конвекционного тока в зазоре второго резонатора.
Далее вычислим основные характеристики: форму волны конвекционного тока в выходном зазоре и максимальный электронный КПД двухрезонаторного клистрона.
2.1.3. Форма волны конвекционного тока в пространстве дрейфа и выходном зазоре
При идеальных сетках в обоих зазорах можно допустить, что число электронов, попадающих на сетки, пренебрежимо мало. Попаданием электронов на стенки трубы дрейфа также пренебрежем, считая, что на пучок наложено бесконечно большое постоянное магнитное поле. Таким образом, можно считать, что средний конвекционный ток пучка одинаков в любом сечении. В соответствии с законом сохранения заряда
dq1 =dq2;i1dt1 =i2dt2 , (2.12)
где i1,i2 – соответственно мгновенные значения конвекционного тока пучка в центре первого и второго зазоров.
Конвекционный ток, поступающий во второй резонатор, оказывается равным
i2 =i1![]() ,
(2.13)
,
(2.13)
так как можно считать, что в непосредственной близости от первого зазора модуляция пучка по плотности еще не развилась и i1 =I0.
Следовательно, для определения мгновенного
конвекционного тока достаточно найти
производную
![]() .
.
Из уравнения (2.6) можно получить
![]() .
(2.14)
.
(2.14)
Подставляя это выражение в уравнение (2.13 ), имеем
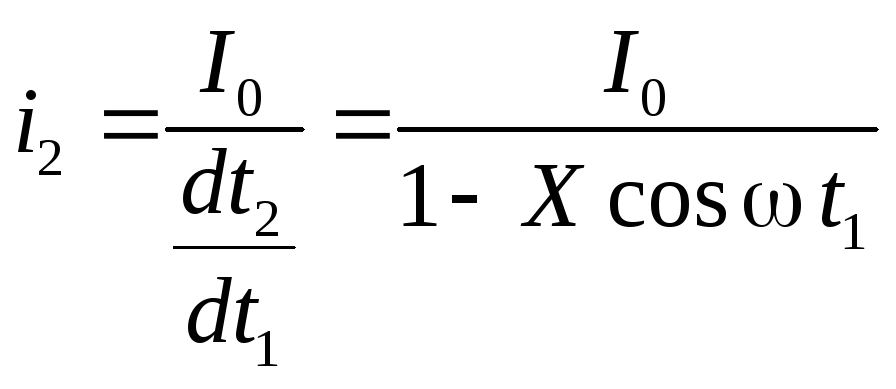 . (2.15)
. (2.15)
Из этого выражения следует, что i2 зависит от времени периодически, но несинусоидально. Для удобства рассмотрения токаi2в функции времениt2обозначимwt1 =j, а также введем новые обозначения в уравнениях (2.11 ) и (2.15 )
1 – Xcos wt1 = y; (2.16)
wt2 – = x. (2.17)
Тогда уравнения (2.15) и (2.11) принимают вид:
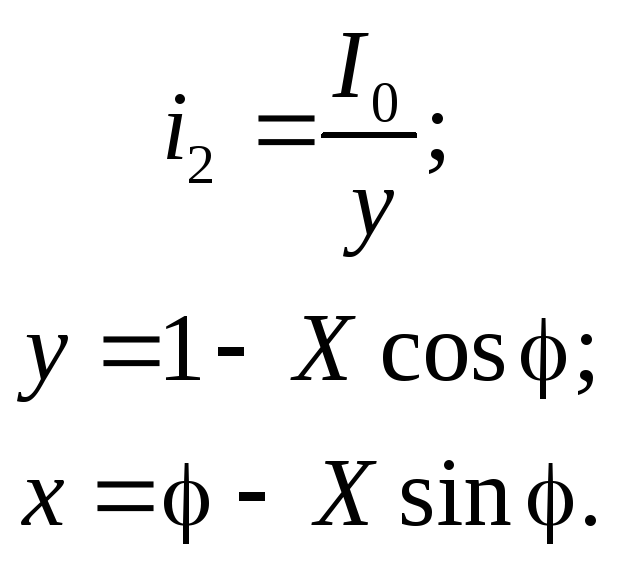 (2.18)
(2.18)
Форма данных уравнений совпадает с хорошо известной параметрической записью уравнений трохоиды – кривой, описываемой точкой, которая находится на фиксированном расстоянии от центра круга, катящегося без скольжения по плоскости.
Таким образом, ток i2по уравнению
(2.18) может рассматриваться как обратная
функция трохоиды при единичном радиусе
катящегося круга. Аргументом является
переменнаяx, которая по уравнению
(2.17) линейно связана с временемt2.
Это означает, что в дальнейшем вместо
интересующей нас функции i2 =
f(t2) оказывается достаточным
проанализировать зависимость![]() .
.
|
Возможны три типичных случая, определяемых величиной параметра группировки Х. ПриХ< 1, т. е. приr<R, точкаА, описывающая трохоиду, расположена внутри катящегося круга (см. рис. 2.3). Кривая не касается осих, и, следовательно, токi2 =f(t2) имеет конечную величину при любых значенияхх, как показанона рис. (2.3,а). Если Х = = 1, то рассматриваемая точка находится на окружности радиуса R. Кривая, описываемая точкой А, является обычной циклоидой (рис. 2.3,б). В точках, где циклоида касается оси абсцисс, ток i2 = =f(х), построенный для этогослучая на рис. 2.4,б, имеет |
Рис. 2.3. Три типичных случая трохоиды, определяющих форму волны тока в клистроне |
| |
|
Рис. 2.4. Форма волны конвекционного тока в двухрезонаторном клистроне |
острый пик, уходящий в бесконечность. При Х > 1, т. е. приr>R, трохоида при каждом обороте круга дважды пересекает осьх. Это означает, что обратная ей функция тока должна иметь два острых пика. Расстояние между пиками должно быть тем больше, чем больше величинаХ. Случай Х > 1 представляет трудности для нахождения графика токаi2 =f(t2). Как видно из рис. 2.3,в, в некотором интервале измененияхвозможны двузначность или трехзначность функцииy =f(x). Сам по себе факт неоднозначности | ||
функции y =f(x) легко объяснить, если обратиться к рис. 2.2. С физической точки зрения эта неоднозначность соответствует одновременному прохождению через выходной зазор нескольких групп электронов, вышедших из группирователя в разные моменты времениt1. Таким образом, имеет место обгон одних групп электронов другими группами и последующее наложение нескольких групп в выходном зазоре. Отметим, что приХ£1 обгон отсутствует.
Для определения конвекционного тока в выходном зазоре в режиме перегона необходимо суммировать токи, созданные каждой из накладывающихся электронных групп. Тогда уравнения (2.13) и (2.18) будут записаны в виде
![]() .
(2.19)
.
(2.19)
Форма волны конвекционного тока при Х> 1 качественно изображена на рис. 2.4,в. Таким образом, переменная составляющая конвекционного тока, получаемая в результате группировки электронов, имеет в общем случае несинусоидальный характер. В системе координат, связанной с центром одного из сгустков и двигающейся со скоростьюv0, наблюдаются постепенно нарастающие уплотнения электронов. Форма этих уплотнений постепенно изменяется соответственно увеличению параметраХ.
Ток i2, представленный на рис. 2.4, характеризует лишь группировку электронов в пучке. Для определения высокочастотной мощности, выделяющейся во втором резонаторе, необходимо получить выражение для наведенного тока, обусловленного конвекционным током в зазоре второго резонатора. Вопрос о том, какой ток будет наведен электронами в выходном зазоре, должен решаться с учетом свойств выходного зазора.
2.1.4. Мощность колебаний в выходном резонаторе
Предположим, что собственная частота резонатора равна частоте сигнала, подведенного к первому резонатору. В этом случае колебания в резонаторе возбуждаются только первой гармоникой наведенного тока, вызванной первой гармоникой конвекционного тока.
По закону сохранения энергии энергия СВЧ колебаний в резонаторе может появиться только из-за уменьшения кинетической энергии электронного потока, проходящего через зазор. Но электроны уменьшают свою кинетическую энергию (скорость), если движутся в тормозящем электрическом поле. Таким образом, необходимо сделать вывод, что появляющееся при возбуждении колебаний в резонаторе напряжение между сетками должно оказывать тормозящее воздействие на проходящий электронный сгусток, т. е. напряжение на зазоре должно находиться в противофазе с первой гармоникой конвекционного тока.
Зазор между сетками, в котором проходит модулированный по плотности электронный поток, эквивалентен источнику энергии СВЧ колебаний, а колебательный контур – нагрузке, где эта энергия расходуется. Зазор можно рассматривать как генератор наведенного тока, величина которого определяется конвекционным током и коэффициентом взаимодействия промодулированного по плотности электронного потока с выходным зазором М2n.
Внешней цепью для наведенного тока в нашем случае можно считать полость тороида. Обычно резонатор заменяют эквивалентным контуром с емкостью Си индуктивностьюL, которые определяются для резонатора, изображенного на рис. 2.1,a, таким образом [2]:
![]() ,
(2.20)
,
(2.20)
![]() . (2.21)
. (2.21)
Можно считать, что емкость определяется
зазором между сетками резонатора, а
индуктивность – полостью тороида, так
как электрическое поле сосредоточено
в зазоре, а магнитное – внутри тороида.
Следовательно, наведенный ток в
эквивалентной схеме проходит через
индуктивность L. Емкостный ток,
появляющийся при наличии между электродами
переменного напряжения и равный![]() ,
также течет во внешней цепи зазора, т.
е. через индуктивностьL. Другими
словами, во внешней цепи течет полный
ток, состоящий из наведенного и емкостного
токов. Составим эквивалентную схему
возбуждения выходного резонатора (рис.
2.5). Резонатор заменен колебательным
контуром с емко-
,
также течет во внешней цепи зазора, т.
е. через индуктивностьL. Другими
словами, во внешней цепи течет полный
ток, состоящий из наведенного и емкостного
токов. Составим эквивалентную схему
возбуждения выходного резонатора (рис.
2.5). Резонатор заменен колебательным
контуром с емко-
Рис. 2.5. Эквивалентная схема возбуждения выходного резонатора
стью С, индуктивностьюLи сопротивлениемR, учитывающим потери в резонаторе и нагрузке. СеткиС/иС// на рис. 2.5 условны, они изображают зазор, через который пролетают сгруппированные электроны. Таким образом, возбуждение выходного резонатора модулированным по плотности электронным потоком можно рассматривать как прохождение первой гармоники наведенного тока через параллельный контур.


