
Вопросы к коллоквиуму
.docxСдаем коллоквиум!
Вопросы:
-
Множества событий. Операции над событиями: сумма, пересечение, разность. Свойства операций. Достоверные и невозможные события. Противоположное событие.
-
Дискретное вероятностное пространство. Схемы с конечным и счетным множествами исходов. Построение пространства элементарных исходов. Аксиоматическое определение вероятности (модель Колмогорова).
-
Формула классической вероятности. Классическое определение вероятности, как частный случай модели Колмогорова.
-
Зависимые и независимые события. Условная вероятность.
-
Формула полной вероятности и формула Байеса.
-
Схема независимых испытаний Бернулли (биномиальная и полиномиальная).
-
Дискретная случайная величина. Функция и ряд распределения случайной величины. Свойства функции распределения. Условие нормировки.
Вывод формулы вычисления вероятности попадания СВ Х в полуинтервал.
-
Основные характеристики дискретной случайной величины: математическое ожидание, дисперсия, мода, среднеквадратическое отклонение.
-
Совместное распределение двух случайных величин.
-
Теоремы о числовых характеристиках.
-
Ковариация и корреляция двух случайных величин. Зависимость и независимость СВ
-
Условные распределения. Условное математическое ожидание. (На примере системы двух дискретных СВ)
-
Дискретные распределения: биномиальное распределение, геометрическое распределение, распределение Пуассона. Проверка выполнения условия нормировки. Подсчет основных числовых характеристик.
-
Функция и плотность распределения непрерывной случайной величины. Свойства. Подсчет вероятности попадания СВ в интервал.
-
Основные характеристики непрерывных случайных величин: математическое ожидание, дисперсия, среднеквадратическое отклонение, мода, медиана, асимметрия и эксцесс.
-
Непрерывные распределения: равномерное распределение, нормальное распределение, показательное распределение, логарифмическое распределение. Подсчет числовых характеристик указанных распределений. Подсчет вероятности попадания СВ, имеющих указанные распределения, в интервал.
Все, что жирным шрифтом, выводим и доказываем)))
Типовые задачи:
-
В урне 5 красных и 1 синий шар. Два шара укатилось. После этого из урны вынимают 1 шар. Он оказался красным. Найти вероятность того, что укатилось 2 красных шара.
-
В двух урнах по 5 белых и 1-му синему шару. Из первой во вторую перекладывают 3 шара. Затем из второй урны вынимают 1 шар. Он оказался синим. Найти вероятность того, что переложили 3 белых шара.

-
Элементы схемы работают независимо и вероятность годности каждого одинакова. Известно, что вероятность прохождения сигнала равна 15/64. Найти вероятность годности каждого элемента.
4. Каждый из 10-ти путников независимо
друг от друга пытаются попасть из А в
В. Направление движения на перекрестках
выбирается случайным образом. Найти
вероятность того, что хотя бы один из
них доберется из А в В.
5. События А, В, С независимы и
реализуются с одинаковой вероятностью
p. Найти
 ,
,

6. Три стрелка делают залп по мишени. Вероятность попадания в цель каждым стрелком одинакова и равна p. Найти вероятность того, что 3-ий стрелок попал в цель, если в цель попало 2-ва снаряда.
7. В группе студентов 15% имеют признак А, 25% - признак В и 10% имеют и признак А и признак В. Найти вероятность того, что из 2-х выбранных студентов хотя бы у одного отсутствуют оба признака.
8. В группе студентов 15% имеют только синие глаза, 30% имеют только темные волосы и 10% имеют и синие глаза и темные волосы. Найти вероятность того, что у вызванного к доске студента с синими глазами будут темные волосы.
9. Завод отправил на базу 1000 изделий. Вероятность повреждения изделия в пути равна 0.001. Найти вероятность того, что в пути повреждено хотя бы одно изделие. Сколько в среднем может быть повреждено при перевозке и с каким разбросом?
10. Из колоды в 36 карт вынимают 4 карты и возвращают их в колоду. Найти вероятность того, что тройка, семерка и туз будут вынуты 3 раза при 5-ти попытках. Сколько раз в среднем будут вынуты тройка, семерка и туз и с каким разбросом?

11. Путник несколько раз пытается попасть из А в В по указанному пути, каждый раз забывая о неудачной попытке. Найти вероятность того, что только с 4-ой попытки он доберется до цели. Сколько в среднем попыток будет сделано и с каким средним отклонением?
12. Для сл. величин
 и
и
 установить зависимость и коррелированность,
найти коэффициент корреляции.
установить зависимость и коррелированность,
найти коэффициент корреляции.

-Найти F(x), M(x), D(x).
- Установить зависимость и коррелированность Х,Y.
-Найти матожидание
 .
.
- Составить ковариационную матрицу и вычислить коэффициент корреляции для V=2X+3Y-2 и S=-X-Y.
-Найти условные средние для Х/Y=0 и Х/Y=1.
13.
 ,
Найти: K;
,
Найти: K;
 ;
;
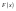 ,
и построить ее график.
,
и построить ее график.
14.
 ,
Найти: А; F(x) и построить ее график,
,
Найти: А; F(x) и построить ее график,
 .
.
15.
 ,
Найти: С; F(x) и построить ее график.
,
Найти: С; F(x) и построить ее график.
16. СВ Х имеет нормальное распределение с параметрами (2,5).
-Записать функцию плотности вероятностей, построить график.
- Вычислить Р(0<Х<1), Р(3<Х<5), Р(0<Х<4), Р(Х<5), Р(Х≥0), Р(Х<1,5)
17. Вычислить вероятность отклонения случайной величины, распределенной нормально с параметрами (а,σ), от своего мат.ожидания на σ, 2σ , 3σ. Сформулировать закон «трех сигм».
