
fiz_osnovy_elektroniki_КЛ[1]
.pdf
ется cos(ka) и ES(k) растѐт, достигая |
|
|
при |
, |
||
точно так же |
изменяется и в интервале |
|
, ширина разрешѐн- |
|||
ной s-зоны: |
|
|
|
|
|
|
|
s |
s max |
s min |
As . |
(4.19) |
|
Для р-состояний |
|
|
|
при |
и |
|
|
при k = 0, а |
|
|
(рис. 4.9). |
|
|
Рис. 4.9. Дисперсионные кривые Е(k) для s- и p-зон
Область значений волнового вектора k, в пределах которого энергия E(k) электрона испытывает полный цикл изменения, называется зонами Бриллюэна. Для одномерного кристалла первая зона Бриллюэна простирается от  до
до  , т.е. протяжѐнность
, т.е. протяжѐнность  .
.
Представляя cos(ka) = 1+ (ka) 2/2 + … и подставляя в (4.17) и (4.18), получим:
E |
s |
k E |
A ka 2 |
, |
|
|
smin s |
|
E |
p |
k |
|
E |
p max |
A (ka)2 |
, |
|||
|
|
|
|
|
|
p |
|
|||
отсюда следует: |
|
|
|
|
|
|
|
|
|
|
E |
дно |
k |
E |
min |
A ka 2 |
(4.20) |
||||
|
|
|
|
|
д |
|
||||
и |
|
|
|
|
|
|
|
|
|
|
E |
верш |
k |
|
|
max |
A (ka)2 |
(4.21) |
|||
|
|
|
|
в |
|
|||||
(квадратичная зависимость от k).
41

Для реального кристалла зависимость E(k), как правило, значительно сложнее (рис. 4.10 а, б и в).
а) |
б) |
в) |
Рис. 4.10. Дисперсионные кривые для Si (а, б) и Ga As (в)
Минимальный зазор между валентной зоной и зоной проводимости принимают за ширину запрещѐнной зоны Eg. Обычно при рассмотрении процессов в полупроводниках зоны изображают как на рис. 4.10 б.
4.5. Эффективная масса электрона
иеѐ зависимость от волнового вектора
|
|
Рассмотрим динамику электрона в |
кристалле. Так как |
||||||||||||
|
|
|
|
, то |
|
! |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
k . |
(4.22) |
|||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
m |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для свободных электронов |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
E |
! |
|
k 2 , |
|
|||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
2m |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
продифференцировав по K, |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
dE |
|
! |
k |
(4.23) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
dk |
|
|
m |
|
||||||
или |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
k |
|
m |
|
|
dE |
, |
(4.24) |
||||
|
|
|
|
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
dk |
|
|||||
|
|
|
|
|
|
|
! |
|
|
|
|||||
42

используя (4.22), получим |
|
|
|
|
|
|
|
V |
1 |
|
dE |
. |
(4.25) |
||
|
|
|
|
||||
|
! |
dk |
|
|
|||
Допустим, что K в (4.24) применимо и для электрона, движущегося |
|||||||
в периодическом поле кристалла. В этом случае |
|
называется квазиим- |
|||||
|
|||||||
пульсом электрона. Если в кристалле создать внешнее электрическое
поле |
|
|
, то это поле действует на электрон с силой |
|
|
|
, сообщая |
||||||||||||||
ему ускорение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
a |
dV |
1 |
|
|
d |
|
dE |
. |
(4.26) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
dt |
|
! |
|
dt |
dk |
|
|
|
|
|||||
|
За время dt сила |
|
производит работу |
|
|
|
или, ис- |
||||||||||||||
|
|
|
|
|
|||||||||||||||||
пользуя (4.25), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
dA |
F |
dE |
dt . |
(4.27) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
! |
dk |
|
|
|
|
|
|
|
|||||
Эта работа идѐт на приращение энергии электрона dE:
dA |
dE |
F |
|
|
dE |
dt |
, |
|
|
|
|
(4.28) |
|||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
! |
|
|
dk |
|
|
|
|
|
|
|
|
||||
отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dk |
|
|
F |
. |
|
|
|
|
|
|
|
|
(4.29) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
dt |
|
! |
|
|
|
|
|
|
|
|
|||||||||
Подставив (4.29) в (4.26), получим |
|
|
|
|
|
|
|
|
|
|
|
или |
|
||||||||
|
|
|
|
|
> |
|
|
> |
|
||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
F |
|
|
|
|
|
! |
|
|
|
, |
|
|
|
|
|
(4.30) |
|||||
|
|
d 2 E dk 2 |
|
|
|
|
|
||||||||||||||
следовательно, выражение |
|
> |
|
|
|
|
|
|
|
представляет собой |
“массу” |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
электрона: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
mэф |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
(4.31) |
|
|
d |
2 E dk 2 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
которую и называют эффективной массой электрона. Приписывая электрону массу эф , мы можем считать этот электрон свободным и
описывать его движение во внешнем поле как обычного свободного
43

электрона. Те же изменения в его движении, которые отличают его от действительно свободного электрона, будут отражать на эф . Эти осо-
бенности приводят к тому, что эф может быть и положительной, и
отрицательной, по абсолютному значению она может быть много больше массы покоя (m) электрона.
1. Истинно свободные электроны. Для них k соответствует (4.24). Подставив (4.24) в (4.31), получим
mэф 
 m m. (4.32)
m m. (4.32)
2. Электроны, находящиеся в периодическом поле решѐтки (квазиэлектроны):
а) Для квазиэлектронов, имеющих энергию, равную дну зоны (4.20),
|
d 2 E |
|
dE |
2Ag a 2 k |
Ag a 2 . |
(4.33) |
||||
|
|
|
|
|
|
|||||
|
dk2 |
|
dk |
|||||||
|
|
|
|
|
|
|||||
Подставляя (4.33) в (4.31), получим: |
|
|
||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
mэф |
|
|
|
. |
(4.34) |
|
|
|
|
|
2Ag a 2 |
|||||
|
|
|
|
|
|
|
|
|||
Так как |
, то |
|
эф |
, т.е. электрон, располагающийся вбли- |
||||||
зи дна зоны, имеет |
эф |
|
|
: чем больше Ag (чем шире зона), тем мень- |
||||||
эф
ше .
б) Энергия электрона вблизи вершины зоны (4.21):
d 2 E |
|
A a 2 |
, |
||||
|
|
|
|||||
dk 2 |
|
в |
|
|
|
||
|
|
|
|
|
|||
т.е. |
|
|
|
|
|
||
|
|
2 |
|
|
|
||
эф |
|
|
|
, |
(4.35) |
||
2А а |
2 |
||||||
|
|
||||||
|
|
|
|
||||
|
|
|
в |
|
|
|
|
отсюда mэф  0. Эти электроны ведут себя аномально: ускоряются во внешнем поле в направлении, противоположном действию внешней силы. Чем шире энергетическая зона, тем меньше |mэф| (рис. 4.11). Почему это происходит: свободный электрон обладает только кинетической энергией, а в кристалле ещѐ и потенциальной, т.е. при движении электрона в кристалле под действием внешней силы F работа этой силы может перейти частью в кинетическую энергию Е к, другая часть – в
0. Эти электроны ведут себя аномально: ускоряются во внешнем поле в направлении, противоположном действию внешней силы. Чем шире энергетическая зона, тем меньше |mэф| (рис. 4.11). Почему это происходит: свободный электрон обладает только кинетической энергией, а в кристалле ещѐ и потенциальной, т.е. при движении электрона в кристалле под действием внешней силы F работа этой силы может перейти частью в кинетическую энергию Е к, другая часть – в
44
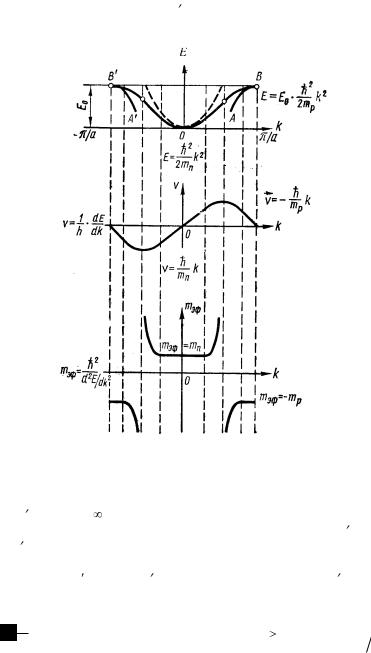
потенциальную U, так что А = Е к + U, т.е. кинетическая энергия будет возрастать медленнее, чем у свободного электрона.
Рис. 4.11. Изменение полной энергии Е(k), скорости, поступательного движения V(k) и эффективной массы mэф электрона
Таким образом, электрон становится как бы тяжелее, если A = U, т.е. dЕ к = 0, mэф = . Наконец, если при движении электрона в потенциальную энергию будет переходить не только вся A(F), но и dЕ к < 0 (U = А + Е к), то электрон будет замедляться, т.е. будет вести себя как частица с mэф < 0. Возможен и такой случай, когда в Eк будет переходить не только A, но и U , так что Е к = А + U, у такого электрона Е
к = А + U, у такого электрона Е к и V будут расти быстрее, чем у свободного, т.е. mэф < m. У дна зоны (k = 0) пока с увеличением k энергия Е(k) растет примерно пропорционально k2,
к и V будут расти быстрее, чем у свободного, т.е. mэф < m. У дна зоны (k = 0) пока с увеличением k энергия Е(k) растет примерно пропорционально k2,
V dE |
растет пропорционально k, ускорение a 0 и |
эф |
|
, |
|
||||
dk |
|
|
||
|
|
|
||
45
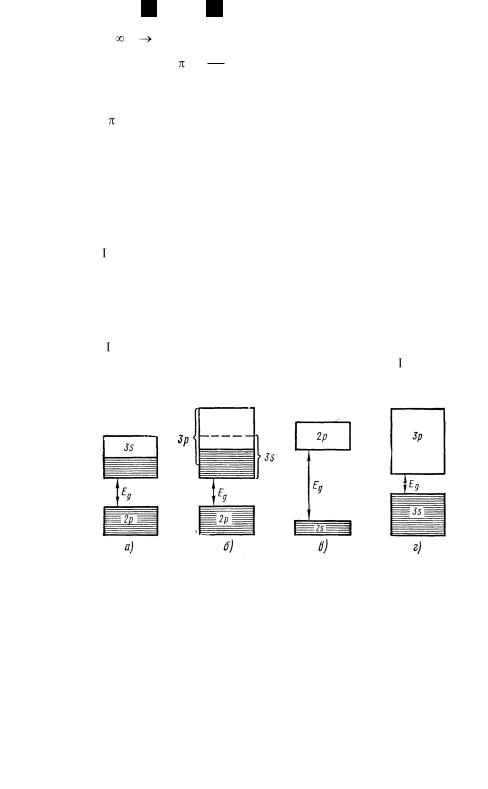
т.е. mn сохраняет положительное значение в точке А перегиба кривой
Е(k), |
d 2 E |
, а |
|
, поэтому при приближении к этой точке |
dk 2 |
|
|||
|
|
|
|
mэф 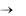 , V Vmax.
, V Vmax.
Далее k  /а, dEdk убывает, поэтому V убывает, т.е. ускорение
/а, dEdk убывает, поэтому V убывает, т.е. ускорение
а<0, а F сохраняет направление, т.е. mф < 0, при этом может изменяться и величина mэф, если меняется кривизна кривой Е(k). У вершины зоны (k =  /а) mэф достигает постоянного отрицательного значения mn.
/а) mэф достигает постоянного отрицательного значения mn.
4.6. Необходимое и достаточное условие для электропроводности
На рис. 4.6 а, б в мы познакомились со схемой расположения энергетических зон для Li, Be и Si. По характеру заполнения зон электронами все тела можно разделить на две большие группы:
. Тела, у которых над целиком заполненными зонами располагается зона, заполненная лишь частично (рис. 4.12 а) (например щелочные металлы). Частично заполненная зона может образоваться и вследствие наложения заполненных зон на пустые или частично заполненные зоны (рис. 4.12 б) (наличие зоны, заполненной лишь частично, присуще металлам).
 . Тела, у которых над целиком заполненными зонами находятся пустые (рис. 4.12 в, г), типичными являются элементы V группы – углерод (алмаз), Si, Ge, Sn (серое олово, имеющее структуру алмаза).
. Тела, у которых над целиком заполненными зонами находятся пустые (рис. 4.12 в, г), типичными являются элементы V группы – углерод (алмаз), Si, Ge, Sn (серое олово, имеющее структуру алмаза).
Рис. 4.12. Варианты строения энергетических зон
К этой же группе относятся многие химические соединения – окислы металлов, нитриды, карбиды, галогениды щелочных металлов
46

и т.д. Согласно зонной теории внешние электроны могут свободно перемещаться по кристаллу как в металлах, так и в диэлектриках. Однако для металлов  = 10-7 Ом-1, а у хороших диэлектриков
= 10-7 Ом-1, а у хороших диэлектриков  = 10-11 Ом-1. Таким образом, наличие свободных электронов, способных перемещаться по кристаллу, является необходимым, но недостаточным условием для появления электропроводности. Чтобы сформулировать достаточное условие, рассмотрим поведение электронов во внешнем поле. Создадим внешнее поле . На каждый электрон действует сила F=eE, которая стремится создать симметрию в распределении электронов по скоростям, пытаясь затормозить электроны, движущиеся против силы, и ускорить движение в направлении силы. Так как подобное ускорение или замедление связано с изменением энергии электрона, то это означает переход электрона в новые квантовые состояния с большей или меньшей энергией. Такие переходы могут осуществ-
= 10-11 Ом-1. Таким образом, наличие свободных электронов, способных перемещаться по кристаллу, является необходимым, но недостаточным условием для появления электропроводности. Чтобы сформулировать достаточное условие, рассмотрим поведение электронов во внешнем поле. Создадим внешнее поле . На каждый электрон действует сила F=eE, которая стремится создать симметрию в распределении электронов по скоростям, пытаясь затормозить электроны, движущиеся против силы, и ускорить движение в направлении силы. Так как подобное ускорение или замедление связано с изменением энергии электрона, то это означает переход электрона в новые квантовые состояния с большей или меньшей энергией. Такие переходы могут осуществ-
ляться, очевидно, лишь в том случае, если в энергетической зоне, к которой принадлежат эти электроны, имеются свободные состояния, т.е. зона заполнена не полностью. Далее слабое поле спо-
собно сообщить электронам  группы добавочный импульс, чтобы перевести их на ближайшие свободные уровни. В кристалле появится преимущественное движение электронов против поля, т.е. электрический ток. Во
группы добавочный импульс, чтобы перевести их на ближайшие свободные уровни. В кристалле появится преимущественное движение электронов против поля, т.е. электрический ток. Во  группе свободные состояния отделены от заполненных состояний энергетической щелью. Следовательно, E не изменит характер движения электронов в валентной зоне. Поле E не способно поднять электроны в свободную зону. Внутри зоны оно может вызвать лишь перестановку электронов местами, что не нарушит симметрии распределения электронов по скоростям, т.е. направленного движения электронов не будет (нулевая электропроводность). Таким образом, достаточным условием появления у тел высокой проводимости является наличие в их энергетическом спектре зон, занятых электронами лишь частично, т.е. как у
группе свободные состояния отделены от заполненных состояний энергетической щелью. Следовательно, E не изменит характер движения электронов в валентной зоне. Поле E не способно поднять электроны в свободную зону. Внутри зоны оно может вызвать лишь перестановку электронов местами, что не нарушит симметрии распределения электронов по скоростям, т.е. направленного движения электронов не будет (нулевая электропроводность). Таким образом, достаточным условием появления у тел высокой проводимости является наличие в их энергетическом спектре зон, занятых электронами лишь частично, т.е. как у 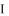 группы.
группы.
По ширине запрещенной зоны Eg тела группы условно делят на диэлектрики и полупроводники. К диэлектрикам относят тела с Eg>1 эВ (алмаз – 5,2 эВ, BN – 4,6 эВ, Al2O3 – 7 эВ и т.д.). У полупроводников узкая запрещенная зона обычно ~ 1эВ (Ge – 0,66 эВ, Si – 1,08 эВ, InSb – 0,17 эВ, GaAs – 1,43 эВ). Так как под действием электрического поля могут переходить электроны, имеющие энергию Ферми, то, следовательно, явление переноса определяется особенностями энергетической зоны вблизи уровня Ферми. Определим число электронных состояний вблизи энергии Ферми, т.е. плотность состояний, но предварительно рассмотрим, как энергия Ферми зависит от числа электронов.
47

4.7. Поверхность Ферми. Число состояний
Функция распределения электронов в кристалле подчиняется распределению Ферми-Дирака:
Е Е |
1 |
|
ф |
Е |
е kT |
1 , |
(4.36) |
|
|
|
|
т.е. в электропроводности участвуют электроны, находящиеся вблизи EF. Выясним число состояний и, соответственно, электронов, участвующих в электропроводности. Энергию можно представить:
|
|
|
|
|
|
p 2 |
|
|
|
|
||
|
|
|
E |
|
|
. |
|
|
|
(4.37) |
||
|
|
2m * |
|
|
|
|||||||
Так как электрон движется вдоль x, y, z, то |
|
|
||||||||||
p |
2 |
2 |
2 |
|
|
2 |
|
(4.38) |
||||
|
|
x |
|
p y |
pz , |
|
||||||
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
px2 |
|
|
p 2y |
|
|
pz2 |
. |
(4.39) |
|
|
2m* |
|
2m* |
|
2m* |
|||||||
|
|
|
|
|
|
|||||||
Электроны заполняют состояния до EF, следовательно, в пространстве импульсов каждому электрону свой импульс. Так как энергия электронов принимает дискретный характер, то из (4.37) следует, что электроны могут обладать дискретными значениями импульса, т.е. каждый электрон обладает определѐнным импульсом, и все электроны должны отличаться друг от друга по импульсу на величину, определяемую принципом неопределѐнности, для рх:
px x h 2 , |
(4.40) |
где рх и х – неопределѐнности импульса и координаты. Если кристалл имеет размер L по x, y, z, то неопределѐнность х = L/2, это максимальная неопределѐнность координаты. Тогда из (4.40) имеем:
px h L – |
(4.41) |
минимальное значение неопределѐнности импульса и |
рy=h/L и рz=h/L. |
Неопределѐнность импульса на рис. 4.14 есть куб с размерами h/L. Минимальное значение объѐма в трѐхмерном импульсном пространстве, характеризующее неопределѐнность импульса, равно
px p y pz h3 L3 . (4.42)
L3 . (4.42)
48
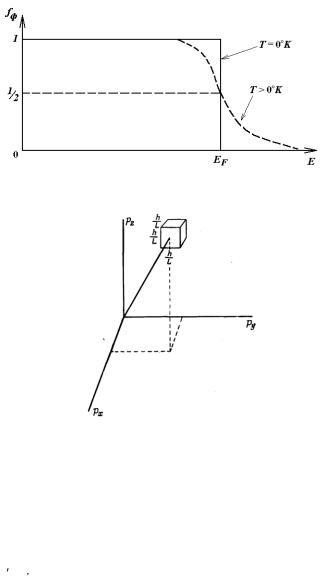
Рис. 4.13. Вид функции Ферми для разных температур
Рис. 4.14. Элемент объема в пространстве импульсов, соответствующий неопределенности трансляционного состояния электрона в зоне
Импульсы всех электронов, имеющих энергию EF, согласно (4.39) лежат на сфере радиусом рF, эта поверхность называется поверхностью Ферми. В энергетической зоне электроны занимают состояние до EF, поэтому импульсы всех электронов, заполняющих эту зону, соответствуют радиус-векторам, лежащим внутри сферы Ферми, а число электронов N =N v, где N – число атомов в объѐме L3, v – число электронов в атоме. Так как
V |
4 |
pF3 , |
(4.43) |
|
3 |
||||
|
|
|
то число состояний равно V/V1, где V – полный объѐм сферы Ферми, а V1 – объѐм 1-го состояния. Так как в каждом состоянии с данным им-
49

пульсом находятся 2 электрона с противоположными спинами ( ), то полное число состояний (с учѐтом степени вырождения gi):
), то полное число состояний (с учѐтом степени вырождения gi):
V |
|
N |
|
|
N v |
|
4 |
|
L3 pF3 |
, |
(4.44) |
||
V |
|
2g |
i |
|
2g |
i |
3 |
|
h |
3 |
|||
|
|
|
|
|
|||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|||
(gs = 1; gp = 3; gd = 5). Отсюда имеем:
|
3 |
|
h3 Nv |
34 |
|
pF |
|
|
|
. |
(4.45) |
8 |
|
L3 gi |
|||
|
|
|
|
Подставив это выражение в (4.37), получим:
|
1 |
|
3 |
|
h3 Nv |
23 |
|
EF |
|
|
|
|
|
. |
(4.46) |
2m* |
8 |
|
L3 gi |
||||
|
|
|
|
||||
(Отступление: объѐм каждого состояния – куб, при EF 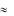 1эВ, для L=1м p=10-34см, поэтому можно считать сферу Ферми гладкой.)
1эВ, для L=1м p=10-34см, поэтому можно считать сферу Ферми гладкой.)
Таким образом, EF определяется (при N = const; L = const) числом электронов в атоме или, обозначив n = N/L3 – число атомов в единице объѐма:
EF |
|
1 |
|
|
|
h3 |
n v |
2 3 |
|||
|
|
|
|
|
|
|
|
|
(4.47) |
||
|
2m * |
|
gi |
||||||||
|
|
|
|
|
|||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
EF |
|
|
h2 |
|
|
3nv |
23 |
. |
||
|
|
2m* |
8 gi |
|
|||||||
|
|
|
|
|
|||||||
4.8. Плотность электронных состояний
Рассмотрим распределение состояний по шкале энергии. Рассмотрим 1-ю зону Бриллюэна в пространстве импульсов. Одному состоянию соответствует объем (h/L)3.
По мере увеличения числа электронов увеличивается число занятых состояний. Внешние состояния соответствуют энергии Ферми, т.е. лежат на сфере Ферми, при этом с увеличением числа электронов объем
сферы Ферми растет. Плотность электронных состояний |
|
|
|
|||||
|
|
|
||||||
(число состояний на единичный интервал Е). Из (4.46) |
|
|
|
|||||
N v |
8 |
2m* E |
32 L3 g |
, |
(4.48) |
|||
|
|
3h3 |
|
|||||
|
|
|
|
|
|
|
|
|
50
